Is 2/3 Greater Than 3/4
saludintensiva
Sep 12, 2025 · 6 min read
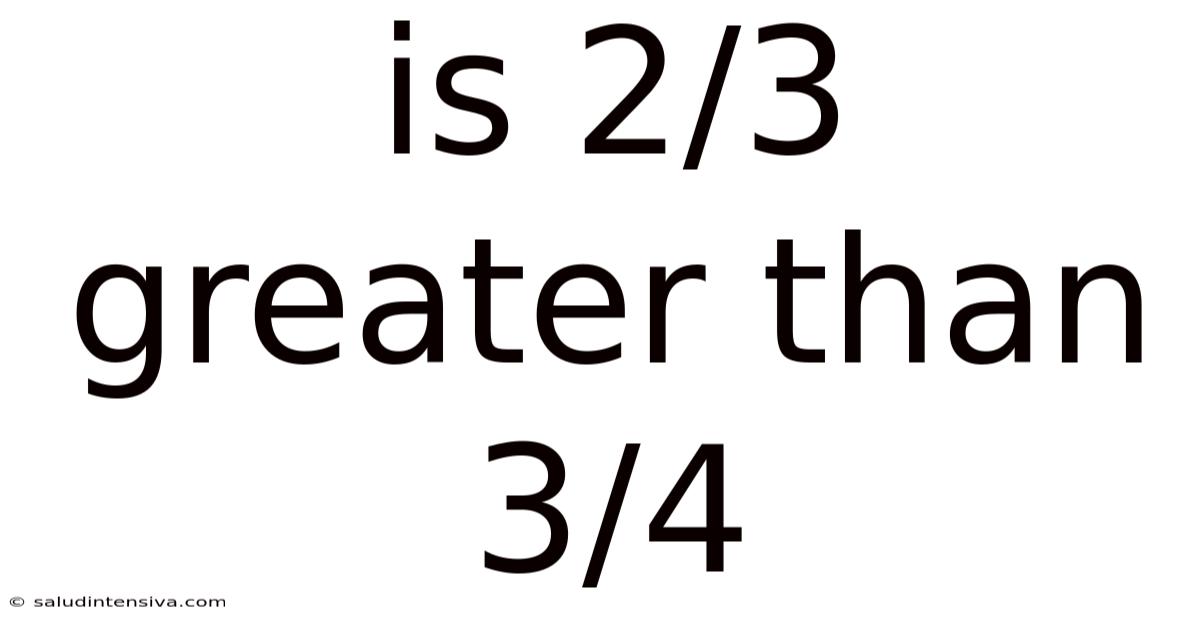
Table of Contents
Is 2/3 Greater Than 3/4? Understanding Fraction Comparison
Is 2/3 greater than 3/4? This seemingly simple question delves into the fundamental concepts of fractions, a crucial area in mathematics. Understanding how to compare fractions is essential not only for academic success but also for everyday problem-solving, from cooking and measuring to budgeting and understanding proportions. This article will thoroughly explore the methods for comparing fractions, focusing on the comparison of 2/3 and 3/4, and will equip you with the skills to tackle similar comparisons confidently.
Understanding Fractions: A Quick Refresher
Before we dive into comparing 2/3 and 3/4, let's refresh our understanding of fractions. A fraction represents a part of a whole. It's composed of two key elements:
- Numerator: The top number, indicating the number of parts we have.
- Denominator: The bottom number, indicating the total number of equal parts the whole is divided into.
For example, in the fraction 2/3, the numerator (2) represents two parts, and the denominator (3) indicates that the whole is divided into three equal parts.
Method 1: Finding a Common Denominator
The most common and reliable method for comparing fractions is to find a common denominator. A common denominator is a number that is a multiple of both denominators. Once both fractions have the same denominator, we can easily compare their numerators.
Let's apply this method to compare 2/3 and 3/4:
-
Find the Least Common Multiple (LCM): The LCM of 3 and 4 is 12. This means we'll convert both fractions to have a denominator of 12.
-
Convert the Fractions:
-
To convert 2/3 to a fraction with a denominator of 12, we multiply both the numerator and denominator by 4: (2 x 4) / (3 x 4) = 8/12
-
To convert 3/4 to a fraction with a denominator of 12, we multiply both the numerator and denominator by 3: (3 x 3) / (4 x 3) = 9/12
-
-
Compare the Numerators: Now that both fractions have the same denominator (12), we can compare their numerators: 8 and 9. Since 8 < 9, we can conclude that 8/12 < 9/12.
-
Conclusion: Therefore, 2/3 is less than 3/4.
Method 2: Converting to Decimals
Another effective method for comparing fractions is to convert them into decimals. This method is particularly useful when dealing with fractions that are difficult to convert to a common denominator.
-
Convert to Decimals:
-
To convert 2/3 to a decimal, divide the numerator (2) by the denominator (3): 2 ÷ 3 ≈ 0.6667 (recurring decimal)
-
To convert 3/4 to a decimal, divide the numerator (3) by the denominator (4): 3 ÷ 4 = 0.75
-
-
Compare the Decimals: Now compare the decimal values: 0.6667 and 0.75. Since 0.6667 < 0.75, we can conclude that 2/3 < 3/4.
-
Conclusion: Once again, we confirm that 2/3 is less than 3/4.
Method 3: Visual Representation
Visual aids can be incredibly helpful, especially when explaining fraction comparison to younger learners or those who benefit from a more intuitive approach. You can use diagrams, such as circles or rectangles, divided into equal parts to represent the fractions.
For instance, draw two circles. Divide the first circle into three equal parts and shade two of them to represent 2/3. Divide the second circle into four equal parts and shade three of them to represent 3/4. By visually comparing the shaded areas, it becomes apparent that 3/4 represents a larger portion than 2/3.
This method provides a concrete, easily understandable representation of the fraction comparison, strengthening the understanding of the concept.
Method 4: Cross-Multiplication
Cross-multiplication offers a more algebraic approach to comparing fractions. This method is particularly efficient when dealing with larger numbers or more complex fractions.
-
Cross-Multiply: Multiply the numerator of the first fraction by the denominator of the second fraction, and vice versa.
- 2/3 and 3/4: (2 x 4) = 8 and (3 x 3) = 9
-
Compare the Products: Compare the two products: 8 and 9. The larger product corresponds to the larger fraction. Since 8 < 9, we know that 2/3 < 3/4.
-
Conclusion: This method confirms that 2/3 is less than 3/4.
The Importance of Understanding Fraction Comparison
The ability to accurately compare fractions is crucial for a wide range of applications:
- Mathematics: It's a fundamental skill in algebra, geometry, and calculus.
- Science: Essential for understanding ratios, proportions, and scientific measurements.
- Everyday Life: Used in cooking, baking, measuring, budgeting, and understanding percentages.
Mastering fraction comparison not only improves mathematical proficiency but also enhances problem-solving skills across various domains.
Frequently Asked Questions (FAQ)
Q: Are there other methods for comparing fractions?
A: Yes, although the methods described above are the most common and effective, other techniques exist, such as converting fractions to percentages or using number lines to visually compare their positions. However, these methods often rely on the underlying principles of common denominators or decimal conversions.
Q: What if the fractions have the same numerator?
A: If two fractions have the same numerator, the fraction with the smaller denominator is the larger fraction. For example, 2/3 is greater than 2/5 because a whole divided into fewer parts (3) results in larger parts compared to a whole divided into more parts (5).
Q: What if the fractions have the same denominator?
A: If two fractions have the same denominator, the fraction with the larger numerator is the larger fraction. For instance, 3/4 is greater than 2/4 because it represents a greater number of parts out of the same whole.
Q: Can I use a calculator to compare fractions?
A: Yes, calculators can assist in converting fractions to decimals, making comparisons straightforward. However, understanding the underlying principles of fraction comparison is crucial for solving problems without reliance on technology.
Q: Why is understanding fraction comparison important for higher-level math?
A: A solid understanding of fraction comparison lays the foundation for more advanced mathematical concepts. It's crucial for working with rational numbers, solving equations, and understanding more complex algebraic expressions.
Conclusion: 2/3 is NOT Greater Than 3/4
Through various methods – finding a common denominator, converting to decimals, visual representation, and cross-multiplication – we have definitively shown that 2/3 is less than 3/4. Mastering these methods will empower you to confidently compare any pair of fractions and unlock a deeper understanding of this fundamental mathematical concept. Remember, consistent practice and a clear understanding of the underlying principles are key to mastering fraction comparison. Don't hesitate to revisit these methods and practice with different fraction pairs to solidify your understanding. The ability to compare fractions is a valuable tool that will benefit you across various aspects of your life, both academic and practical.
Latest Posts
Latest Posts
-
Formula For Final Kinetic Energy
Sep 12, 2025
-
What Is Equivalent To 3 2
Sep 12, 2025
-
Can 3 5 Be Simplified
Sep 12, 2025
-
Least Common Multiple Of 40
Sep 12, 2025
-
6 24 As A Percentage
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about Is 2/3 Greater Than 3/4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.