What Is Equivalent To 3/2
saludintensiva
Sep 12, 2025 · 5 min read
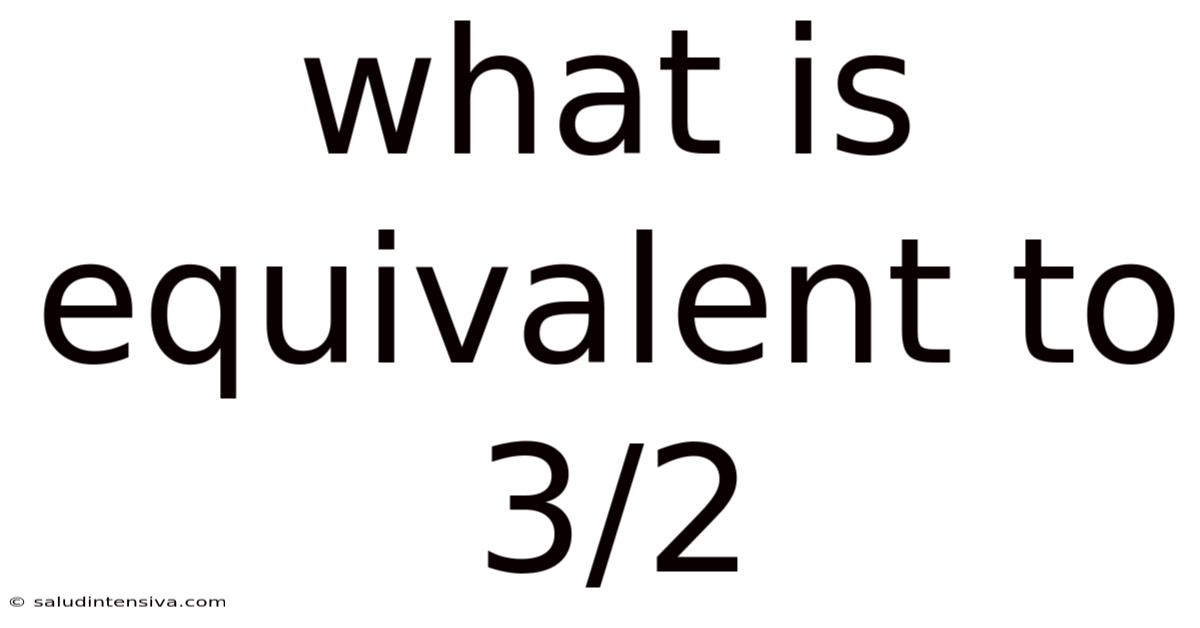
Table of Contents
What is Equivalent to 3/2? Unlocking the World of Fractions and Equivalents
Understanding fractions is a cornerstone of mathematical literacy. This comprehensive guide delves into the question: what is equivalent to 3/2? We'll explore not only the simple answer but also the underlying principles of fraction equivalence, different representations, and practical applications. This will equip you with a robust understanding of this fundamental concept. We will also touch upon related topics such as improper fractions, mixed numbers, decimals, and percentages, showing you how they all interconnect.
Introduction: Understanding Fractions and Equivalence
The fraction 3/2 represents a ratio or a part of a whole. The top number, 3, is the numerator, indicating the number of parts we have. The bottom number, 2, is the denominator, representing the total number of equal parts the whole is divided into. Because the numerator is larger than the denominator, 3/2 is considered an improper fraction. This means it represents a value greater than one whole.
Finding an equivalent fraction means finding another fraction that represents the same value. This is achieved by multiplying or dividing both the numerator and denominator by the same non-zero number. This process doesn't change the overall value of the fraction, just its representation.
Finding Equivalents: The Multiplication Method
The most straightforward method to find equivalents of 3/2 is to multiply both the numerator and the denominator by the same number. Let's try a few examples:
- Multiply by 2: (3 x 2) / (2 x 2) = 6/4
- Multiply by 3: (3 x 3) / (2 x 3) = 9/6
- Multiply by 4: (3 x 4) / (2 x 4) = 12/8
- Multiply by 5: (3 x 5) / (2 x 5) = 15/10
All of these fractions – 6/4, 9/6, 12/8, 15/10, and infinitely more – are equivalent to 3/2. They all represent the same quantity, just expressed differently. This highlights the fundamental principle of fraction equivalence: multiplying the numerator and denominator by the same number doesn't alter the fraction's value.
Finding Equivalents: The Division Method (Simplification)
While multiplication generates larger equivalent fractions, division (also known as simplification) produces smaller ones. We can't directly simplify 3/2 to a smaller equivalent fraction with whole numbers because 3 and 2 share no common factors other than 1. However, this concept is crucial for understanding the relationship between improper fractions and mixed numbers, which we’ll explore in the next section. If we had a fraction like 6/4, we could divide both the numerator and denominator by 2 to simplify it to 3/2.
Representing 3/2: Mixed Numbers and Decimals
Improper fractions, like 3/2, can be represented in two other useful forms: mixed numbers and decimals.
Mixed Numbers: A mixed number combines a whole number and a proper fraction. To convert 3/2 to a mixed number, we perform division:
3 ÷ 2 = 1 with a remainder of 1.
This means 3/2 is equivalent to 1 and 1/2 (written as 1 1/2). The whole number represents how many whole "2s" are contained within 3, and the fraction represents the remaining part.
Decimals: Converting a fraction to a decimal involves dividing the numerator by the denominator:
3 ÷ 2 = 1.5
Therefore, 3/2 is equivalent to 1.5. This decimal representation is particularly useful for calculations and comparisons.
Visualizing Equivalence: Geometric Representation
Imagine a pizza cut into two equal slices. The fraction 3/2 represents having three of these slices. This is more than one whole pizza. Now, imagine the same pizza cut into four equal slices. To have the same amount of pizza, you'd need six slices (6/4). Similarly, cutting the pizza into six equal slices would require nine slices (9/6) to represent the same quantity. This visual representation clearly demonstrates the concept of equivalent fractions. Each fraction represents the same amount of pizza, but the slices are simply of different sizes.
Beyond the Basics: Applications and Advanced Concepts
The concept of fraction equivalence is crucial in many areas, including:
- Cooking and Baking: Following recipes often requires understanding and adjusting fraction sizes.
- Construction and Engineering: Precise measurements rely on fractional calculations.
- Finance and Accounting: Working with percentages and ratios necessitates a strong understanding of fractions.
- Data Analysis: Representing proportions and percentages in data often involves working with fractions.
Understanding fraction equivalence also lays the groundwork for more advanced mathematical concepts:
- Algebra: Solving equations and simplifying expressions often involves manipulating fractions.
- Calculus: Differential and integral calculus builds upon the foundational understanding of fractions and limits.
Frequently Asked Questions (FAQ)
Q: Are there infinitely many fractions equivalent to 3/2?
A: Yes, absolutely. You can multiply the numerator and denominator by any non-zero number to create a new equivalent fraction.
Q: How do I choose the "best" equivalent fraction?
A: The "best" equivalent fraction often depends on the context. Sometimes a simplified fraction is preferred (like 3/2). Other times, a fraction with a specific denominator might be more convenient for calculations.
Q: Can a fraction have more than one equivalent representation?
A: Yes, every fraction (except for 0/1) has an infinite number of equivalent representations.
Q: What is the difference between simplifying and reducing a fraction?
A: Simplifying and reducing a fraction are essentially the same thing: dividing both the numerator and denominator by their greatest common divisor (GCD) to obtain the smallest equivalent fraction with whole number terms.
Conclusion: Mastering Fraction Equivalence
The seemingly simple question "What is equivalent to 3/2?" opens a door to a deeper understanding of fractions, their various representations (improper fractions, mixed numbers, decimals), and their significance in various fields. Mastering the concept of equivalence is not just about memorizing procedures; it's about grasping the fundamental principle that different representations can express the same quantity. This understanding is pivotal for success in mathematics and its numerous applications in the real world. By understanding how to find equivalents through multiplication and division, and by visualizing the concept geometrically, you gain a robust and versatile tool for tackling mathematical challenges with confidence. Remember the core principle: Multiplying or dividing both the numerator and denominator by the same non-zero number results in an equivalent fraction. With practice and a solid understanding of the underlying principles, you can confidently navigate the world of fractions and their equivalents.
Latest Posts
Latest Posts
-
Gcf Of 60 And 60
Sep 12, 2025
-
13 16 As A Decimal
Sep 12, 2025
-
14 Acres To Sq Ft
Sep 12, 2025
-
List Of Multiples Of 8
Sep 12, 2025
-
Lcm Of 25 And 35
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about What Is Equivalent To 3/2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.