Is 2/3 More Than 1/4
saludintensiva
Sep 22, 2025 · 5 min read
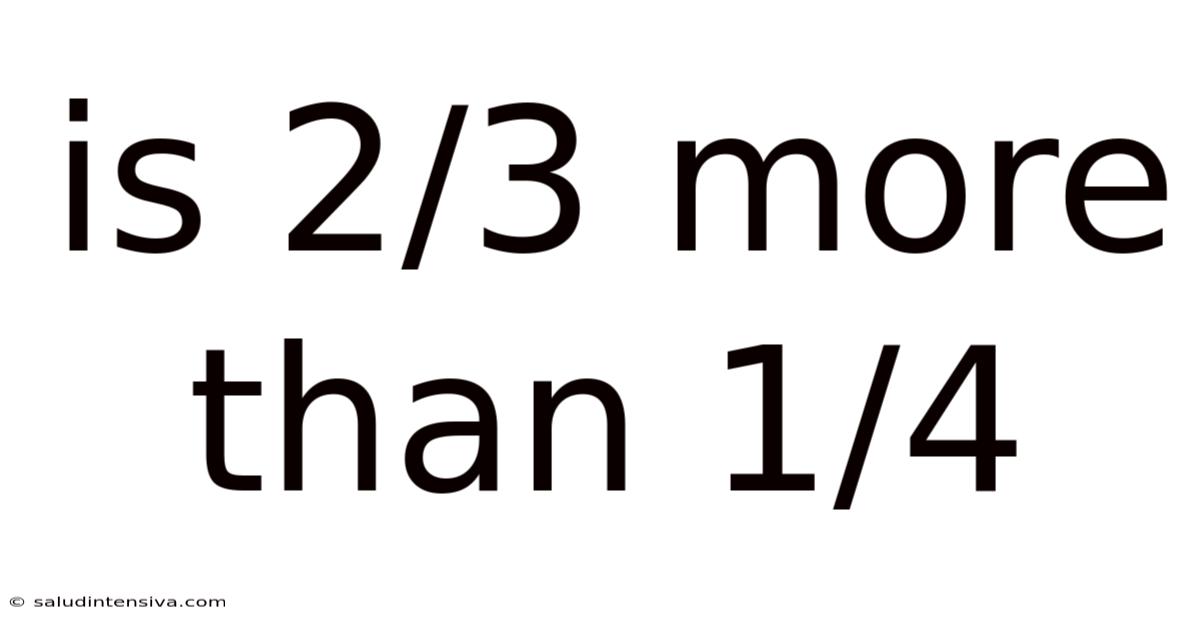
Table of Contents
Is 2/3 More Than 1/4? A Deep Dive into Fraction Comparison
This article explores the seemingly simple question: is 2/3 more than 1/4? While the answer might seem obvious to some, understanding how to determine the relative size of fractions is crucial for a solid grasp of mathematical concepts. We'll delve into various methods for comparing fractions, explaining the underlying principles in a clear and accessible manner. This will equip you not only to answer this specific question but also to confidently tackle more complex fraction comparisons in the future.
Understanding Fractions: A Quick Refresher
Before diving into the comparison, let's refresh our understanding of fractions. A fraction represents a part of a whole. It's composed of two numbers: the numerator (the top number) and the denominator (the bottom number). The numerator indicates how many parts we have, while the denominator indicates how many equal parts the whole is divided into. For example, in the fraction 2/3, the numerator is 2 and the denominator is 3. This means we have 2 parts out of a total of 3 equal parts.
Method 1: Visual Comparison using Diagrams
One of the simplest ways to compare fractions is by visualizing them. Let's represent 2/3 and 1/4 using diagrams:
2/3: Imagine a circle divided into three equal parts. Shade two of these parts.
+---+---+---+
| | | |
+---+---+---+
shaded: 2/3
1/4: Now, imagine another circle divided into four equal parts. Shade one of these parts.
+---+---+---+---+
| | | | |
+---+---+---+---+
shaded: 1/4
By visually comparing the shaded areas, it's clear that 2/3 represents a larger portion of the whole than 1/4.
Method 2: Finding a Common Denominator
A more formal method involves finding a common denominator. This means finding a number that is a multiple of both denominators (3 and 4). The least common multiple (LCM) of 3 and 4 is 12. We then convert both fractions to equivalent fractions with a denominator of 12:
-
2/3: To change the denominator from 3 to 12, we multiply both the numerator and the denominator by 4: (2 x 4) / (3 x 4) = 8/12
-
1/4: To change the denominator from 4 to 12, we multiply both the numerator and the denominator by 3: (1 x 3) / (4 x 3) = 3/12
Now, comparing 8/12 and 3/12 is straightforward. Since 8 is greater than 3, 8/12 (which is equivalent to 2/3) is greater than 3/12 (which is equivalent to 1/4).
Method 3: Converting Fractions to Decimals
Another approach involves converting the fractions to decimals. This is done by dividing the numerator by the denominator:
-
2/3: 2 ÷ 3 ≈ 0.6667
-
1/4: 1 ÷ 4 = 0.25
Comparing the decimal values, 0.6667 is clearly larger than 0.25. Therefore, 2/3 is greater than 1/4.
Method 4: Cross-Multiplication
Cross-multiplication provides a concise method for comparing fractions. We multiply the numerator of the first fraction by the denominator of the second fraction and vice-versa. Then, we compare the results:
-
2/3 ? 1/4
-
(2 x 4) ? (1 x 3)
-
8 ? 3
Since 8 > 3, 2/3 is greater than 1/4.
The Importance of Understanding Fraction Comparison
The ability to compare fractions is fundamental to many areas of mathematics and beyond. It's essential for:
-
Solving equations: Many algebraic equations involve fractions, and comparing their relative sizes is crucial for finding solutions.
-
Data analysis: Understanding fractions is vital for interpreting data represented in fractional form, such as percentages or proportions.
-
Real-world applications: Fractions are used extensively in everyday life, from cooking and construction to finance and engineering. The ability to compare them allows us to make informed decisions.
Addressing Common Misconceptions
A common misconception is that simply looking at the numerators or denominators independently is sufficient to determine which fraction is larger. This is incorrect. Consider the fractions 1/2 and 1/10. Although the numerator of 1/10 is smaller, 1/2 is actually larger because it represents a greater portion of the whole.
Frequently Asked Questions (FAQ)
Q: Can I compare fractions with different denominators directly without finding a common denominator?
A: No, directly comparing fractions with different denominators can lead to incorrect conclusions. Finding a common denominator or converting to decimals ensures accurate comparison.
Q: Is there a fastest method for comparing fractions?
A: The fastest method often depends on the specific fractions involved and your familiarity with different techniques. Cross-multiplication is generally quick for simple fractions, while converting to decimals can be efficient with a calculator.
Q: What if the fractions are negative?
A: When comparing negative fractions, remember that the larger the absolute value, the smaller the fraction. For example, -1/2 is greater than -2/3 because -1/2 is closer to zero on the number line.
Q: How can I improve my understanding of fractions?
A: Practice is key! Work through numerous examples, use visual aids like diagrams, and try different comparison methods to build your confidence and understanding.
Conclusion: 2/3 is Indeed Greater Than 1/4
Through various methods – visual comparison, common denominators, decimal conversion, and cross-multiplication – we've definitively established that 2/3 is greater than 1/4. Understanding the different approaches to comparing fractions is not just about solving a single problem; it's about developing a strong foundation in mathematical reasoning and problem-solving that will serve you well in many aspects of life. The key takeaway is to understand the why behind the comparison, not just the what. This ensures a deeper and more lasting comprehension of fractional relationships. Remember to practice regularly and explore different techniques to solidify your grasp of this fundamental mathematical concept.
Latest Posts
Latest Posts
-
16 Hours From 8 Pm
Sep 22, 2025
-
18 Min Mile In Mph
Sep 22, 2025
-
4 To The 4 Power
Sep 22, 2025
-
10 Yard Concrete Truck Cost
Sep 22, 2025
-
Square Root Of 28 Simplified
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about Is 2/3 More Than 1/4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.