Is 2/5 Greater Than 1/4
saludintensiva
Sep 10, 2025 · 5 min read
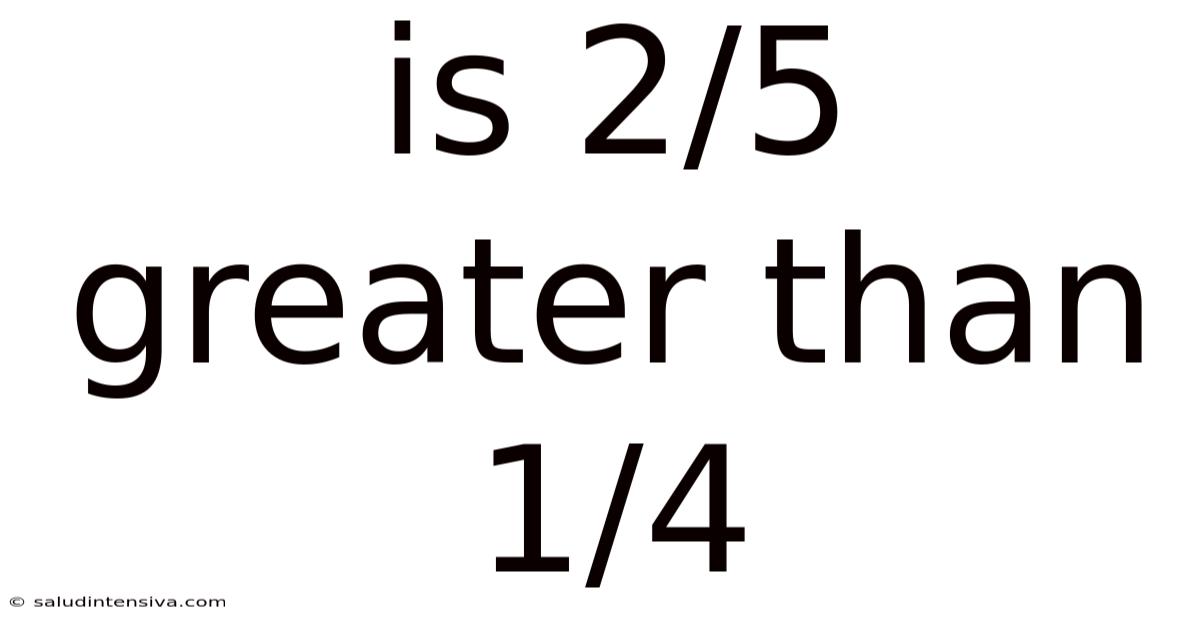
Table of Contents
Is 2/5 Greater Than 1/4? A Deep Dive into Fraction Comparison
Is 2/5 greater than 1/4? This seemingly simple question opens the door to a deeper understanding of fractions, a fundamental concept in mathematics. This article will not only answer this question definitively but also explore various methods for comparing fractions, providing you with the tools to confidently tackle similar problems in the future. We'll delve into different approaches, from visual representations to numerical calculations, ensuring you grasp the underlying principles.
Understanding Fractions: A Quick Refresher
Before we tackle the comparison, let's refresh our understanding of fractions. A fraction represents a part of a whole. It's written as a numerator (the top number) over a denominator (the bottom number), like this: a/b. The numerator (a) indicates how many parts we have, and the denominator (b) indicates how many equal parts the whole is divided into. For example, in the fraction 1/4, the numerator 1 represents one part, and the denominator 4 indicates that the whole is divided into four equal parts.
Method 1: Visual Comparison using Diagrams
A visual approach is often the most intuitive way to compare fractions, especially for beginners. Let's represent 2/5 and 1/4 using diagrams:
2/5: Imagine a rectangle divided into five equal parts. Shade two of these parts to represent 2/5.
[Imagine a rectangle divided into 5 equal parts, with 2 parts shaded]
1/4: Now, imagine another rectangle of the same size, divided into four equal parts. Shade one of these parts to represent 1/4.
[Imagine a rectangle divided into 4 equal parts, with 1 part shaded]
By visually comparing the shaded areas, it's evident that the shaded area representing 2/5 is larger than the shaded area representing 1/4. Therefore, 2/5 is greater than 1/4.
Method 2: Finding a Common Denominator
A more precise method involves finding a common denominator for both fractions. A common denominator is a number that is a multiple of both denominators. In this case, the denominators are 5 and 4. The least common multiple (LCM) of 5 and 4 is 20.
To convert 2/5 to an equivalent fraction with a denominator of 20, we multiply both the numerator and denominator by 4:
(2/5) * (4/4) = 8/20
Similarly, to convert 1/4 to an equivalent fraction with a denominator of 20, we multiply both the numerator and denominator by 5:
(1/4) * (5/5) = 5/20
Now we can compare the two fractions: 8/20 and 5/20. Since 8 is greater than 5, 8/20 is greater than 5/20. Therefore, 2/5 is greater than 1/4.
Method 3: Converting to Decimals
Another effective method is to convert both fractions into decimals. To do this, we simply divide the numerator by the denominator:
2/5 = 2 ÷ 5 = 0.4
1/4 = 1 ÷ 4 = 0.25
Comparing the decimal values, 0.4 is greater than 0.25. Therefore, 2/5 is greater than 1/4. This method provides a clear numerical comparison, making it easy to understand the relative sizes of the fractions.
Method 4: Cross-Multiplication
Cross-multiplication offers a quick way to compare two fractions. We multiply the numerator of the first fraction by the denominator of the second fraction, and vice-versa. Then, we compare the results.
For 2/5 and 1/4:
2 * 4 = 8
5 * 1 = 5
Since 8 > 5, we conclude that 2/5 > 1/4.
Why Understanding Fraction Comparison is Crucial
The ability to compare fractions is not just a mathematical skill; it's a fundamental building block for many areas of life. From understanding recipes (e.g., determining which ingredient requires a larger quantity) to analyzing data (e.g., interpreting percentages and proportions), comparing fractions is essential for making informed decisions.
Extending the Concept: Comparing More Complex Fractions
The methods described above can be applied to compare more complex fractions as well. For example, let's consider comparing 7/12 and 5/8.
Finding a common denominator: The LCM of 12 and 8 is 24.
7/12 = (7/12) * (2/2) = 14/24
5/8 = (5/8) * (3/3) = 15/24
Since 15/24 > 14/24, we conclude that 5/8 > 7/12.
Converting to decimals:
7/12 ≈ 0.583
5/8 = 0.625
Again, 0.625 > 0.583, confirming that 5/8 > 7/12.
Cross-multiplication:
7 * 8 = 56
12 * 5 = 60
Since 60 > 56, we conclude that 5/8 > 7/12.
Frequently Asked Questions (FAQs)
Q: What if the fractions have different denominators and I can't easily find a common denominator?
A: You can still use the decimal conversion method or cross-multiplication. Finding the least common multiple (LCM) might take a bit more time, but it's a reliable way to achieve accurate comparison.
Q: Is there a shortcut for comparing fractions if one numerator and one denominator are the same?
A: Not a universally applicable shortcut, but if you have fractions like 3/5 and 4/5, comparing the numerators directly suffices, since the denominator is the same. Similarly, for fractions like 3/7 and 3/8, you can directly compare the denominators.
Q: How can I explain fraction comparison to a young child?
A: Using visual aids like pizzas or chocolate bars divided into equal pieces is highly effective. Let the child physically represent each fraction and compare the sizes of the shaded areas.
Q: Can I use a calculator to compare fractions?
A: Yes, calculators can convert fractions to decimals, making comparison straightforward.
Conclusion
Determining whether 2/5 is greater than 1/4, or comparing any two fractions, requires understanding the underlying principles of fractions and employing appropriate comparison methods. We've explored several techniques, each offering a unique approach to problem-solving. Whether you prefer visual representations, finding common denominators, converting to decimals, or employing cross-multiplication, mastering these methods will empower you to tackle fraction comparison confidently and effectively. Remember, the choice of method depends on your comfort level and the complexity of the fractions involved. The key is to choose a method you understand well and apply it consistently to obtain accurate results. By strengthening your understanding of fractions, you unlock a critical skill applicable in various aspects of life beyond the classroom.
Latest Posts
Latest Posts
-
5 1 4 As A Decimal
Sep 11, 2025
-
What Is 2 3 Of 5
Sep 11, 2025
-
300 000 Minutes To Hours
Sep 11, 2025
-
3 1 2 1 2
Sep 11, 2025
-
Gcf Of 32 And 36
Sep 11, 2025
Related Post
Thank you for visiting our website which covers about Is 2/5 Greater Than 1/4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.