Is 2/5 Greater Than 2/3
saludintensiva
Sep 09, 2025 · 5 min read
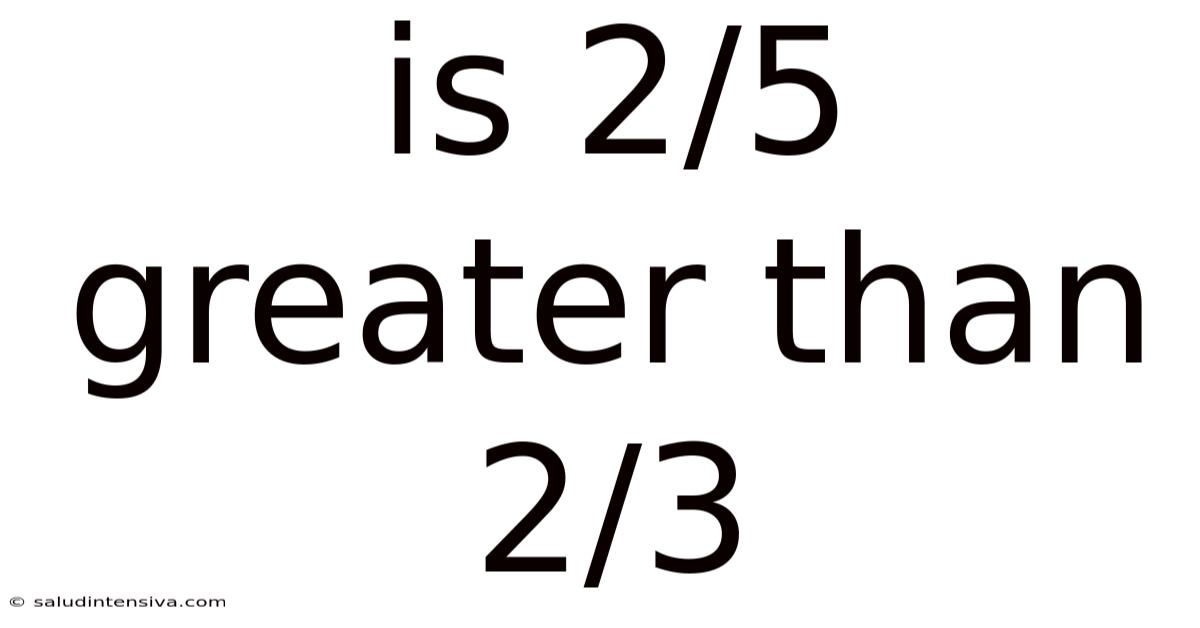
Table of Contents
Is 2/5 Greater Than 2/3? Understanding Fractions and Comparisons
This article delves into the seemingly simple question: Is 2/5 greater than 2/3? While the answer might appear obvious to some, understanding the underlying principles of comparing fractions is crucial for developing a strong foundation in mathematics. We'll explore various methods for comparing fractions, providing a clear and comprehensive explanation suitable for learners of all levels. This includes visual representations, numerical comparisons, and a deeper understanding of fraction concepts.
Introduction to Fractions
Before diving into the comparison, let's refresh our understanding of fractions. A fraction represents a part of a whole. It's written in the form a/b, where 'a' is the numerator (the number of parts we have) and 'b' is the denominator (the total number of equal parts the whole is divided into). For example, in the fraction 2/5, 2 is the numerator and 5 is the denominator. This means we have 2 out of 5 equal parts.
Visualizing Fractions: A Pictorial Approach
One of the most effective ways to understand fraction comparisons is through visualization. Let's represent 2/5 and 2/3 visually using diagrams:
Imagine a rectangle divided into five equal parts. Shading two of these parts represents 2/5.
[Insert image here: A rectangle divided into 5 equal parts, with 2 parts shaded]
Now, imagine another rectangle, this time divided into three equal parts. Shading two of these parts represents 2/3.
[Insert image here: A rectangle divided into 3 equal parts, with 2 parts shaded]
By visually comparing the shaded areas, it becomes clear that the shaded area representing 2/3 is larger than the shaded area representing 2/5. This provides a simple, intuitive understanding of which fraction is greater.
Numerical Comparison Methods
While visual representation is helpful, particularly for beginners, numerical methods offer a more precise and generalizable approach to comparing fractions. Here are three common methods:
1. Finding a Common Denominator: This is arguably the most common and reliable method. The goal is to rewrite both fractions with the same denominator. To do this, we find the least common multiple (LCM) of the denominators.
The denominators are 5 and 3. The LCM of 5 and 3 is 15 (because 3 x 5 = 15 and 15 is the smallest number divisible by both 3 and 5).
Now, we rewrite each fraction with a denominator of 15:
- 2/5 = (2 x 3) / (5 x 3) = 6/15
- 2/3 = (2 x 5) / (3 x 5) = 10/15
Since 10/15 > 6/15, we can conclude that 2/3 > 2/5.
2. Converting to Decimals: Another method involves converting both fractions to decimals and comparing the decimal values.
- 2/5 = 0.4
- 2/3 = 0.666... (a repeating decimal)
Since 0.666... > 0.4, it confirms that 2/3 > 2/5.
3. Cross-Multiplication: This method offers a quick way to compare fractions without finding a common denominator. We cross-multiply the numerators and denominators:
- 2/5 ? 2/3
Cross-multiply: (2 x 3) ? (2 x 5)
This simplifies to: 6 ? 10
Since 6 < 10, we conclude that 2/5 < 2/3.
Understanding the Underlying Principle
The reason 2/3 is greater than 2/5 lies in the concept of the denominator. The denominator indicates the size of each part. A smaller denominator means that the whole is divided into fewer, larger parts. In our example, the whole is divided into three parts in 2/3 and five parts in 2/5. Since each part in 2/3 is larger than each part in 2/5, taking two parts from 2/3 results in a larger quantity than taking two parts from 2/5.
Expanding the Concept: Comparing Fractions with Different Numerators and Denominators
The methods described above can be applied to compare any two fractions, even those with different numerators and denominators. Let's consider another example: Is 3/4 greater than 5/8?
Using the common denominator method:
The LCM of 4 and 8 is 8.
- 3/4 = (3 x 2) / (4 x 2) = 6/8
- 5/8 remains as 5/8
Since 6/8 > 5/8, we conclude that 3/4 > 5/8.
Using the decimal method:
- 3/4 = 0.75
- 5/8 = 0.625
Since 0.75 > 0.625, we reach the same conclusion.
Using cross-multiplication:
- 3/4 ? 5/8
- (3 x 8) ? (5 x 4)
- 24 ? 20
Since 24 > 20, we again confirm that 3/4 > 5/8.
Frequently Asked Questions (FAQ)
Q: Why is finding a common denominator the most reliable method?
A: Finding a common denominator ensures that we are comparing equal-sized pieces. This eliminates any ambiguity and provides a consistent and accurate comparison regardless of the complexity of the fractions.
Q: Can I use a calculator to compare fractions?
A: Yes, most calculators can handle fraction calculations. You can convert the fractions to decimals and compare the decimal values directly.
Q: What if I have more than two fractions to compare?
A: You can use the same methods to compare multiple fractions. Find a common denominator for all fractions and then compare the numerators. Alternatively, convert all fractions to decimals and compare the decimal values.
Q: Are there any shortcuts for comparing simple fractions?
A: For simple fractions with the same numerator, the fraction with the smaller denominator is the larger fraction. For example, 2/3 > 2/5.
Q: What are some real-world applications of comparing fractions?
A: Comparing fractions is essential in various real-world situations, including:
- Baking and cooking: Measuring ingredients accurately.
- Construction and engineering: Precise measurements and calculations.
- Finance: Understanding proportions and percentages.
- Data analysis: Interpreting data represented as fractions.
Conclusion: Mastering Fraction Comparisons
Comparing fractions is a fundamental skill in mathematics. While the initial question, "Is 2/5 greater than 2/3?", may seem simple, understanding the underlying principles of fractions and employing different comparison methods is crucial for solving more complex problems. By mastering these techniques, you'll develop a strong mathematical foundation that will serve you well in various academic and real-world scenarios. Remember to practice regularly to build confidence and proficiency in comparing fractions. The more you practice, the easier and more intuitive this process will become. The visual method helps build foundational understanding, while the numerical methods offer precision and generalizability for all fraction comparisons.
Latest Posts
Latest Posts
-
Ai Lottery Number Generator Free
Sep 09, 2025
-
5 6 As A Percent
Sep 09, 2025
-
Fractions Equivalent To 5 10
Sep 09, 2025
-
How Long Is 111 Minutes
Sep 09, 2025
-
25 6 As A Mixed Number
Sep 09, 2025
Related Post
Thank you for visiting our website which covers about Is 2/5 Greater Than 2/3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.