Is 3/16 Smaller Than 1/4
saludintensiva
Sep 14, 2025 · 6 min read
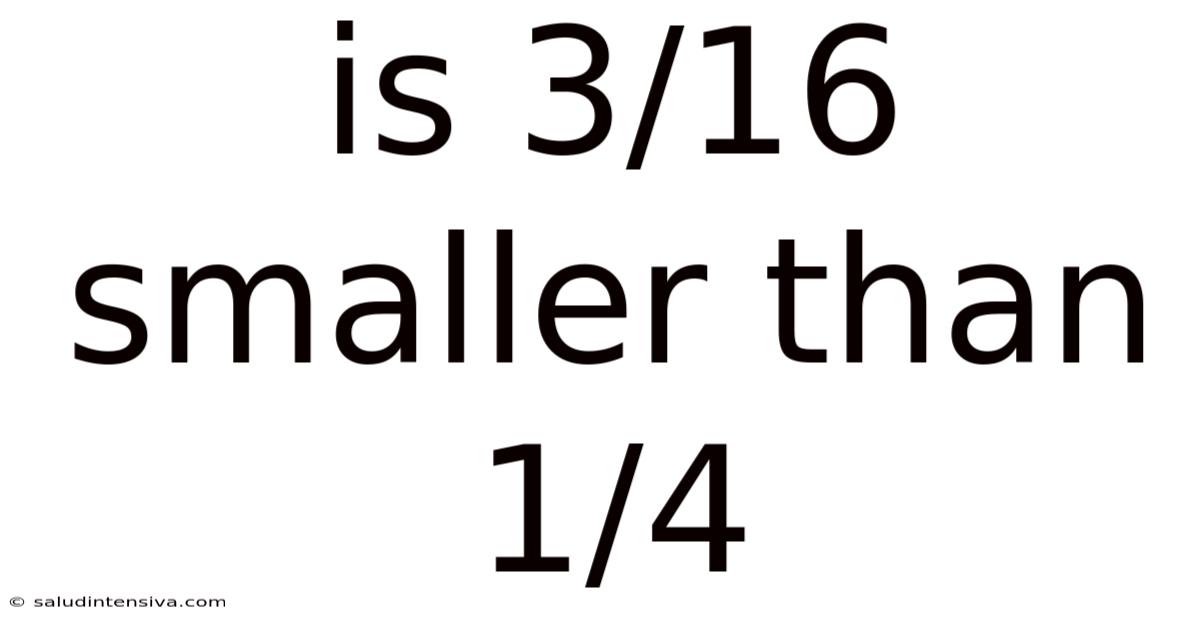
Table of Contents
Is 3/16 Smaller Than 1/4? A Deep Dive into Fraction Comparison
Understanding fractions is a fundamental skill in mathematics, crucial for various applications in daily life and advanced studies. This article will thoroughly explore the comparison of 3/16 and 1/4, providing not only a definitive answer but also a comprehensive understanding of the methods used to compare fractions, including explanations for different learning styles and levels of understanding. We'll delve into the core concepts, providing a step-by-step guide, practical examples, and frequently asked questions to solidify your grasp of fraction comparison. By the end, you'll be confident in comparing any two fractions.
Introduction: Understanding Fractions
Before we tackle the specific comparison of 3/16 and 1/4, let's refresh our understanding of fractions. A fraction represents a part of a whole. It's written as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). The denominator tells us how many equal parts the whole is divided into, while the numerator tells us how many of those parts we're considering. For example, in the fraction 3/4, the whole is divided into 4 equal parts, and we're looking at 3 of those parts.
Comparing 3/16 and 1/4: The Direct Approach
The simplest way to compare 3/16 and 1/4 is to find a common denominator. A common denominator is a number that both denominators (16 and 4) can divide into evenly. In this case, 16 is a common denominator because 4 goes into 16 evenly (4 x 4 = 16).
-
Converting 1/4: To convert 1/4 to a fraction with a denominator of 16, we multiply both the numerator and the denominator by 4: (1 x 4) / (4 x 4) = 4/16.
-
Comparison: Now we can easily compare 3/16 and 4/16. Since 3 is less than 4, we conclude that 3/16 is smaller than 4/16, and therefore, 3/16 is smaller than 1/4.
Visual Representation: Understanding Fractions Through Pictures
Visual aids are excellent tools for grasping fractional concepts. Imagine a pizza cut into 16 slices. 3/16 represents 3 slices of that pizza. Now imagine another pizza, this time cut into 4 slices. 1/4 represents 1 slice of that pizza. While the slices of the first pizza are smaller, 1/4 of the second pizza is still larger than 3/16 of the first. This visual comparison reinforces the mathematical conclusion.
Decimal Conversion: Another Approach to Fraction Comparison
Another method involves converting both fractions into decimals. This approach can be particularly helpful when dealing with more complex fractions or when you prefer working with decimals.
-
Converting 3/16: Divide the numerator (3) by the denominator (16): 3 ÷ 16 = 0.1875
-
Converting 1/4: Divide the numerator (1) by the denominator (4): 1 ÷ 4 = 0.25
-
Comparison: Comparing the decimal values, 0.1875 is less than 0.25. This confirms that 3/16 is smaller than 1/4.
Cross-Multiplication: A Powerful Technique for Fraction Comparison
Cross-multiplication is a powerful technique for comparing any two fractions. It's particularly useful when finding a common denominator is challenging.
-
Cross-multiply: Multiply the numerator of the first fraction (3) by the denominator of the second fraction (4): 3 x 4 = 12.
-
Cross-multiply: Multiply the numerator of the second fraction (1) by the denominator of the first fraction (16): 1 x 16 = 16.
-
Comparison: Compare the results: 12 < 16. The smaller product corresponds to the smaller fraction. Therefore, 3/16 is smaller than 1/4.
Understanding the Concepts: Why This Works
These methods all rely on the fundamental principle of maintaining equivalent fractions. When we multiply or divide both the numerator and the denominator of a fraction by the same number (other than zero), we create an equivalent fraction that represents the same value. This allows us to manipulate fractions until we can easily compare them. Whether we find a common denominator, convert to decimals, or use cross-multiplication, the underlying principle remains the same.
Expanding the Understanding: Comparing Fractions with Different Denominators
The techniques discussed above are applicable to comparing any two fractions, regardless of their denominators. The key is to find a method that works best for you and the specific fractions you are comparing. For instance:
-
Fractions with easily identifiable common denominators: Use the common denominator method.
-
Fractions where finding a common denominator is challenging: Use cross-multiplication or decimal conversion.
-
Fractions involving large numbers: Decimal conversion may be the most efficient.
Practical Applications: Real-world Examples of Fraction Comparison
Understanding fraction comparison is essential in numerous real-world situations:
-
Cooking and Baking: Following recipes often requires comparing fractions to ensure accurate measurements.
-
Construction and Engineering: Precise measurements are crucial, and fractions play a vital role.
-
Financial Calculations: Understanding percentages (which are essentially fractions) is critical for managing finances effectively.
-
Data Analysis: Fractions are used extensively in data analysis and statistics.
Frequently Asked Questions (FAQs)
Q1: Can I use a calculator to compare fractions?
A1: Yes, calculators can be very helpful for converting fractions to decimals, which can then be easily compared. However, understanding the underlying mathematical principles is crucial for broader comprehension.
Q2: What if the fractions are negative?
A2: The same principles apply. Remember that negative numbers work in reverse order: a larger negative number is actually smaller than a smaller negative number. For instance, -3/16 is greater than -1/4.
Q3: Are there other methods for comparing fractions?
A3: While the methods described above are common and efficient, there are other less frequently used methods, such as using fraction bars for visual comparison or employing more advanced algebraic techniques. The most important aspect is choosing a method that you understand well and that works effectively for you.
Q4: How can I improve my understanding of fractions?
A4: Practice is key! Work through various examples, try different methods, and use visual aids to solidify your understanding. Online resources and educational materials can also be incredibly beneficial.
Conclusion: Mastering Fraction Comparison
Comparing fractions is a fundamental mathematical skill that extends far beyond the classroom. This article has provided a comprehensive guide to comparing fractions, equipping you with various techniques and a deeper understanding of the underlying concepts. Remember, practice is crucial to mastering any mathematical skill. By utilizing the methods outlined above and continuing to practice, you'll build confidence and proficiency in working with fractions. Remember that even seemingly simple comparisons like "Is 3/16 smaller than 1/4?" can lead to a much deeper understanding of fundamental mathematical principles and their wide-ranging applications.
Latest Posts
Latest Posts
-
Hcf Of 15 And 18
Sep 14, 2025
-
Write 2 As A Decimal
Sep 14, 2025
-
Birth Calculator By Death Date
Sep 14, 2025
-
35 Degrees F To C
Sep 14, 2025
-
Lcm Of 3 8 6
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about Is 3/16 Smaller Than 1/4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.