Is 3/4 Equivalent To 9/12
saludintensiva
Sep 20, 2025 · 6 min read
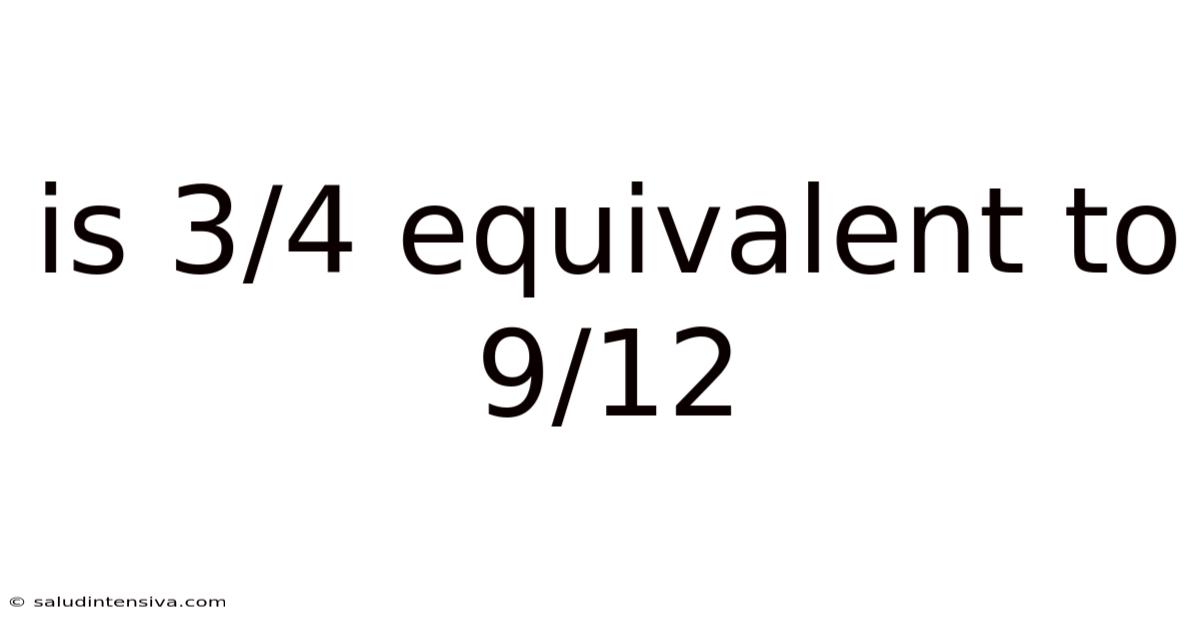
Table of Contents
Is 3/4 Equivalent to 9/12? A Deep Dive into Fraction Equivalence
Understanding fraction equivalence is a fundamental concept in mathematics, crucial for mastering arithmetic, algebra, and beyond. This article will explore the question: Is 3/4 equivalent to 9/12? We'll delve into the principles behind fraction equivalence, providing a thorough explanation supported by examples and addressing frequently asked questions. This comprehensive guide will leave you with a confident grasp of this essential mathematical concept.
Introduction: Understanding Fractions and Equivalence
A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). The denominator indicates how many equal parts the whole is divided into, while the numerator shows how many of those parts are being considered. For example, in the fraction 3/4, the whole is divided into 4 equal parts, and we are considering 3 of those parts.
Two fractions are considered equivalent if they represent the same portion of a whole, even though they may look different. This means they have the same value. Determining equivalence is a key skill in simplifying fractions and performing calculations with them.
Exploring the Equivalence of 3/4 and 9/12
Let's directly address the question: Is 3/4 equivalent to 9/12? The answer is yes. There are several ways to demonstrate this equivalence:
1. Visual Representation: Imagine a pizza cut into four equal slices (representing 3/4). Now imagine another pizza cut into twelve equal slices. If you take nine slices from the second pizza (representing 9/12), you'll have consumed the same amount of pizza as if you'd eaten the three slices from the first pizza. Both fractions represent three-quarters of the whole.
2. Simplifying Fractions: We can simplify a fraction by dividing both the numerator and the denominator by their greatest common divisor (GCD). The GCD of 9 and 12 is 3. Dividing both the numerator and denominator of 9/12 by 3 gives us:
9 ÷ 3 / 12 ÷ 3 = 3/4
This shows that 9/12 simplifies to 3/4, confirming their equivalence.
3. Finding Equivalent Fractions by Multiplication: We can also create equivalent fractions by multiplying both the numerator and the denominator by the same non-zero number. If we multiply both the numerator and denominator of 3/4 by 3, we get:
3 x 3 / 4 x 3 = 9/12
This demonstrates that 3/4 and 9/12 are indeed equivalent fractions.
The Mathematical Principle Behind Fraction Equivalence
The core principle behind fraction equivalence lies in the concept of proportionality. If we multiply or divide both the numerator and the denominator of a fraction by the same non-zero number, the value of the fraction remains unchanged. This is because we're essentially scaling the fraction up or down proportionally.
Consider the fraction a/b. If we multiply both a and b by a non-zero number 'k', we get (a x k) / (b x k). This new fraction is equivalent to the original fraction a/b because:
(a x k) / (b x k) = a/b (The 'k' cancels out)
Similarly, if we divide both a and b by a common divisor 'k', we get (a ÷ k) / (b ÷ k). This simplified fraction is also equivalent to the original fraction.
Steps to Determine Fraction Equivalence
Here's a step-by-step guide to determine if two fractions are equivalent:
-
Simplify both fractions: Reduce each fraction to its simplest form by dividing the numerator and denominator by their greatest common divisor (GCD).
-
Compare the simplified fractions: If the simplified fractions are identical, then the original fractions are equivalent.
-
Cross-multiplication: Another method involves cross-multiplication. Multiply the numerator of the first fraction by the denominator of the second fraction, and vice-versa. If the products are equal, the fractions are equivalent. For example, to check if 3/4 and 9/12 are equivalent:
- 3 x 12 = 36
- 4 x 9 = 36
Since the products are equal, the fractions are equivalent.
Real-World Applications of Fraction Equivalence
Understanding fraction equivalence is crucial in numerous real-world situations:
-
Cooking and Baking: Recipes often require adjustments based on the number of servings. Fraction equivalence helps in accurately scaling up or down ingredient amounts.
-
Measurement and Construction: In construction and engineering, precise measurements are critical. Converting between different units of measurement often involves working with fractions and requires an understanding of equivalence.
-
Finance and Budgeting: Managing finances and creating budgets involves working with percentages and fractions, which relies heavily on the concept of equivalence.
-
Data Analysis: In data analysis and statistics, understanding equivalent fractions is essential for interpreting and comparing proportions and ratios.
Advanced Concepts Related to Fraction Equivalence
While the basic concept is straightforward, several advanced concepts build upon fraction equivalence:
-
Rational Numbers: Fractions are rational numbers, which can be expressed as the ratio of two integers. Understanding equivalence is crucial for manipulating and comparing rational numbers.
-
Decimal Representation: Every fraction has an equivalent decimal representation. Converting between fractions and decimals involves understanding fraction equivalence.
-
Proportion and Ratio: Proportion and ratio problems are closely related to fraction equivalence and require a similar understanding of proportional scaling.
Frequently Asked Questions (FAQ)
Q1: Can any fraction be expressed as an equivalent fraction?
A1: Yes, infinitely many equivalent fractions can be generated for any given fraction by multiplying or dividing the numerator and denominator by the same non-zero number.
Q2: What is the simplest form of a fraction?
A2: The simplest form of a fraction is when the numerator and denominator have no common factors other than 1 (their GCD is 1). It's also known as a fraction in its lowest terms.
Q3: How can I quickly check if two fractions are equivalent?
A3: The fastest method is cross-multiplication. If the product of the numerator of the first fraction and the denominator of the second fraction equals the product of the numerator of the second fraction and the denominator of the first fraction, then the fractions are equivalent. Simplifying fractions first can also make the comparison easier.
Q4: Is it important to simplify fractions?
A4: Yes, simplifying fractions makes them easier to understand, compare, and use in calculations. It also presents the fraction in its most concise form.
Conclusion: Mastering Fraction Equivalence
In conclusion, 3/4 is indeed equivalent to 9/12. This equivalence is not just a coincidence; it's a direct consequence of the fundamental principle of proportionality governing fractions. Understanding this principle and the various methods for determining fraction equivalence are essential for success in mathematics and its diverse applications across various fields. By mastering this core concept, you'll build a strong foundation for more advanced mathematical concepts and problem-solving. Through practice and a thorough understanding of the underlying principles, you'll confidently navigate the world of fractions and their countless applications.
Latest Posts
Latest Posts
-
90 Days From 6 6
Sep 20, 2025
-
X 3 X 5 2
Sep 20, 2025
-
Lbf Ft To Kg M
Sep 20, 2025
-
7 16ths Of An Inch
Sep 20, 2025
-
What Is 220c In Fahrenheit
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about Is 3/4 Equivalent To 9/12 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.