X 3 X 5 2
saludintensiva
Sep 20, 2025 · 5 min read
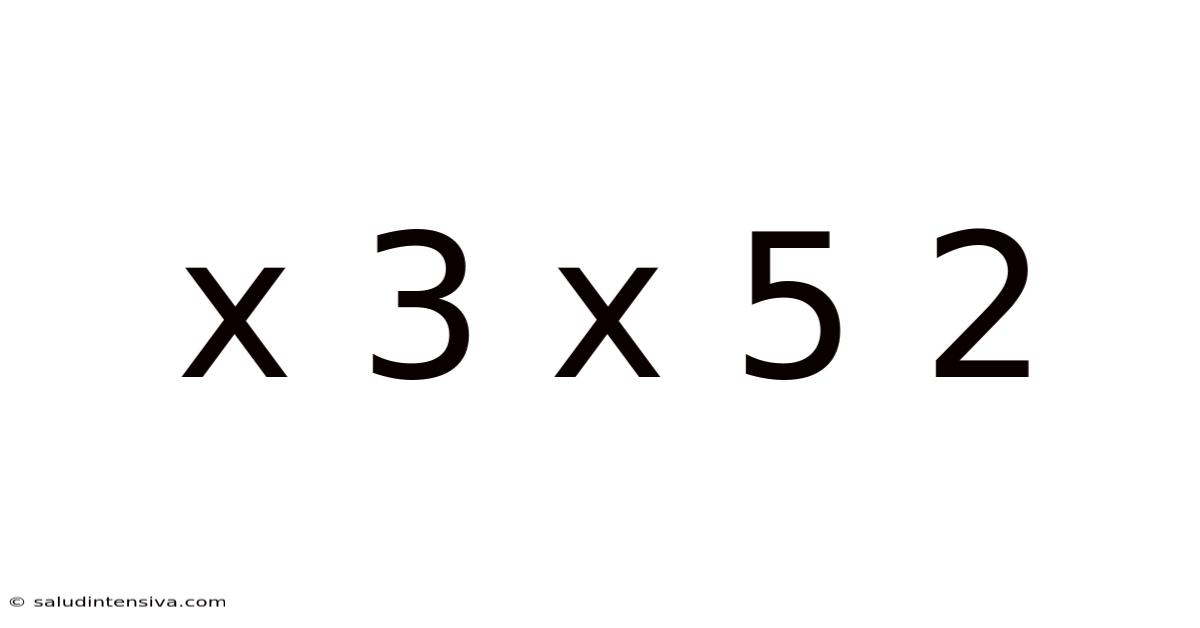
Table of Contents
Decoding the Enigma: A Deep Dive into the Mathematical Expression "x³ x⁵ = 2"
This article explores the mathematical expression x³ x⁵ = 2, delving into its solution, the underlying principles, and its broader implications within algebra. We'll break down the problem step-by-step, examining various methods of solution and addressing common misconceptions. This comprehensive guide is designed for students of algebra, from beginners grappling with exponents to those seeking a deeper understanding of equation solving. By the end, you'll not only understand how to solve this specific equation but also gain a stronger foundation in algebraic manipulation.
Understanding the Fundamentals: Exponents and Algebraic Manipulation
Before tackling the equation x³ x⁵ = 2, let's refresh our understanding of key concepts. The expression involves exponents, which represent repeated multiplication. For instance, x³ means x * x * x, and x⁵ means x * x * x * x * x. The fundamental rule for multiplying terms with the same base and different exponents is to add the exponents: xᵃ * xᵇ = x⁽ᵃ⁺ᵇ⁾.
This rule forms the bedrock of our approach to solving x³ x⁵ = 2. Applying this rule, we can simplify the left-hand side of the equation:
x³ x⁵ = x⁽³⁺⁵⁾ = x⁸
Therefore, our simplified equation becomes:
x⁸ = 2
Solving the Equation: Unveiling the Value of x
Now that we've simplified the equation to x⁸ = 2, we need to isolate x. This requires finding the eighth root of 2. While there's no simple whole number solution, we can express the solution using radicals or approximate it using numerical methods.
Method 1: Using Radicals
The most straightforward approach is to express the solution using the eighth root:
x = ⁸√2
This represents the principal (positive) eighth root of 2. It's an irrational number, meaning it cannot be expressed as a simple fraction.
Method 2: Approximation using Numerical Methods
To obtain an approximate numerical value for x, we can employ various numerical methods. A common approach is using a calculator or computer software to calculate the eighth root of 2:
x ≈ 1.0905
This approximation provides a practical value for x, suitable for many applications. Keep in mind that this is only an approximation; the true value of x is irrational and has infinitely many decimal places.
Exploring the Concept of Roots and Their Multiplicity
The equation x⁸ = 2 actually has eight distinct solutions in the complex number system. While we've focused on the principal root (the positive real root), there are seven other complex roots. These roots are spread around the unit circle in the complex plane. Understanding this concept requires a grasp of complex numbers and De Moivre's theorem, which are beyond the scope of a basic algebraic introduction. However, it's crucial to note that the simplicity of the initial equation belies the rich mathematical landscape underlying its solution.
Expanding the Understanding: Generalizing the Approach
The method used to solve x³ x⁵ = 2 is applicable to a broader class of problems involving exponential equations. Consider a general equation of the form:
xᵃ xᵇ = c
where a, b, and c are constants. Following the same principle of adding exponents, we can simplify this to:
x⁽ᵃ⁺ᵇ⁾ = c
Then, to solve for x, we take the (a+b)th root of c:
x = ⁽ᵃ⁺ᵇ⁾√c
This generalized approach allows us to tackle similar problems with different exponents and constants.
Addressing Common Mistakes and Misconceptions
Several common mistakes can arise when solving exponential equations. Here are some key points to remember:
- Incorrectly combining exponents: A frequent error is subtracting exponents instead of adding them when multiplying terms with the same base. Remember the rule: xᵃ * xᵇ = x⁽ᵃ⁺ᵇ⁾.
- Neglecting negative solutions: While the principal root is often the focus, it's crucial to consider the possibility of negative solutions, especially when dealing with even exponents.
- Misunderstanding irrational numbers: Many students struggle with the concept of irrational numbers and their representation. It's important to grasp that irrational numbers have infinite non-repeating decimal expansions and cannot be expressed as simple fractions.
Practical Applications and Real-World Examples
While this equation might seem abstract, similar exponential equations frequently appear in various fields:
- Physics: Exponential functions model phenomena like radioactive decay and population growth.
- Engineering: Exponential equations are used in circuit analysis and signal processing.
- Finance: Compound interest calculations involve exponential functions.
- Biology: Modeling bacterial growth or the spread of diseases often involves exponential relationships.
Understanding how to solve these equations is fundamental to success in these fields.
Frequently Asked Questions (FAQ)
Q: Can x³ x⁵ = 2 be solved without using radicals or approximations?
A: No, the exact solution involves an irrational number (⁸√2), which cannot be expressed precisely without using radicals. Approximations provide a practical numerical value.
Q: Are there any other solutions besides the principal root?
A: Yes, in the complex number system, there are seven other complex roots. These solutions involve imaginary numbers and are more complex to calculate.
Q: What if the equation was x³ + x⁵ = 2? How would that be solved?
A: This is a different type of equation (a polynomial equation), and its solution requires different techniques, such as numerical methods or the use of advanced algebraic tools. It cannot be solved using the simple exponent rule we used previously.
Q: Why is it important to understand the concept of roots and their multiplicity?
A: Understanding the multiplicity of roots is crucial for comprehending the full solution set of an equation and its behavior. In some applications, all roots might be relevant, not just the principal root.
Conclusion: Mastering Algebraic Manipulation and Beyond
Solving the equation x³ x⁵ = 2 might seem like a small step in the vast world of mathematics. However, it provides a valuable opportunity to reinforce fundamental concepts of exponents, radicals, and algebraic manipulation. By understanding the principles behind its solution, you build a stronger foundation for tackling more complex algebraic problems and further exploring the exciting realm of mathematics and its diverse applications. Remember, the key is to break down complex problems into smaller, manageable steps, and to always double-check your work for accuracy. With practice and perseverance, you'll master these skills and confidently navigate the world of equations.
Latest Posts
Latest Posts
-
What Times What Equals 42
Sep 20, 2025
-
Ml To Gallons Conversion Calculator
Sep 20, 2025
-
Nepali Date Converter To English
Sep 20, 2025
-
90 Days After May 28
Sep 20, 2025
-
December 1 How Many Days
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about X 3 X 5 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.