Is 3/4 Greater Than 3/8
saludintensiva
Sep 18, 2025 · 7 min read
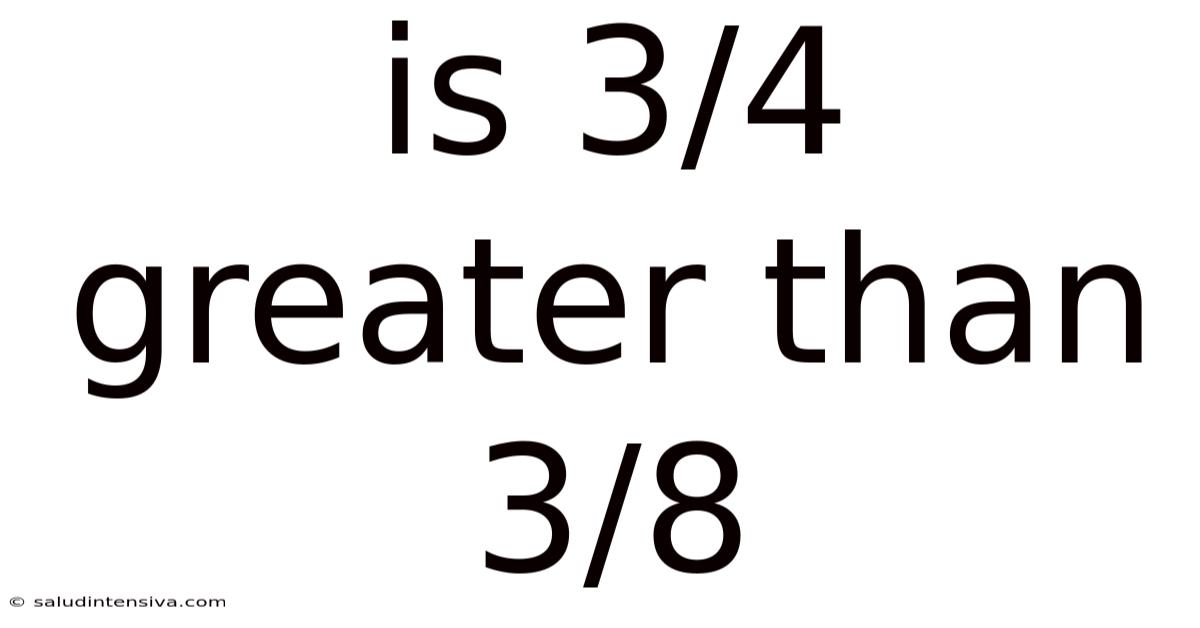
Table of Contents
Is 3/4 Greater Than 3/8? A Deep Dive into Fraction Comparison
This article explores the seemingly simple question: is 3/4 greater than 3/8? While the answer might seem obvious to some, understanding the underlying principles of fraction comparison is crucial for building a strong foundation in mathematics. We'll delve into various methods for comparing fractions, providing a comprehensive explanation suitable for learners of all levels. This will involve exploring visual representations, numerical comparisons, and the concept of equivalent fractions, ensuring a thorough understanding of this fundamental mathematical concept.
Introduction: Understanding Fractions
Before jumping into the comparison, let's refresh our understanding of fractions. A fraction represents a part of a whole. It's written as a numerator (the top number) over a denominator (the bottom number), separated by a line. The numerator indicates how many parts we have, while the denominator shows the total number of equal parts the whole is divided into. For example, in the fraction 3/4, the numerator is 3, and the denominator is 4. This means we have 3 out of 4 equal parts.
Method 1: Visual Comparison using Fraction Circles or Bars
A simple and intuitive way to compare fractions is through visual representations. Imagine two circles, one divided into four equal parts (representing 3/4), and the other divided into eight equal parts (representing 3/8). Shade three parts in each circle. Visually, it becomes immediately clear that the shaded area in the circle representing 3/4 is significantly larger than the shaded area in the circle representing 3/8. This visual demonstration provides a concrete understanding of why 3/4 is greater than 3/8. Similarly, you could use fraction bars to illustrate this comparison. The bar representing 3/4 will be visibly longer than the bar representing 3/8.
Method 2: Finding a Common Denominator
This is a more formal mathematical approach. To compare fractions with different denominators, we need to find a common denominator – a number that is a multiple of both denominators. In our case, the denominators are 4 and 8. Since 8 is a multiple of 4 (4 x 2 = 8), we can easily convert 3/4 into an equivalent fraction with a denominator of 8.
To do this, we multiply both the numerator and the denominator of 3/4 by 2:
(3 x 2) / (4 x 2) = 6/8
Now we can compare 6/8 and 3/8. Since 6 is greater than 3, we conclude that 6/8 (which is equivalent to 3/4) is greater than 3/8.
Therefore, 3/4 > 3/8
Method 3: Comparing Numerators When Denominators are the Same
Once we've converted the fractions to have a common denominator, comparing them becomes straightforward. We simply compare the numerators. The fraction with the larger numerator is the larger fraction. In our case, after converting 3/4 to 6/8, we compare 6 and 3. Since 6 > 3, we know that 6/8 > 3/8, and therefore 3/4 > 3/8.
Method 4: Decimal Conversion
Another approach is to convert the fractions into decimals. This involves dividing the numerator by the denominator.
3/4 = 0.75
3/8 = 0.375
Comparing the decimal values, it’s evident that 0.75 > 0.375. Therefore, 3/4 > 3/8.
Understanding the Concept of Equivalent Fractions
The process of finding a common denominator relies on the concept of equivalent fractions. Equivalent fractions represent the same portion of a whole, even though they have different numerators and denominators. For instance, 3/4, 6/8, 9/12, and 12/16 are all equivalent fractions. They all represent the same amount – three-quarters of a whole. Understanding this principle is key to confidently comparing and manipulating fractions.
Practical Applications: Real-World Examples
The ability to compare fractions isn't just a theoretical exercise; it's a practical skill with numerous real-world applications. Consider these scenarios:
-
Baking: A recipe might call for 3/4 cup of sugar and 3/8 cup of butter. Understanding that 3/4 is greater than 3/8 helps you to easily visualize which ingredient requires a larger quantity.
-
Measurement: When working with measurements (like inches or centimeters), comparing fractions is essential for accuracy and precision.
-
Data Analysis: In analyzing data presented as fractions, the ability to compare them is crucial for drawing accurate conclusions and making informed decisions.
-
Financial Calculations: Many financial calculations involve fractions, particularly in areas like interest rates and investment returns. Understanding fraction comparison allows for accurate computations and informed financial decisions.
Beyond the Basics: Comparing Fractions with Different Numerators and Denominators
The methods described above primarily focused on comparing fractions where only the denominators differed. Let's expand our understanding to include comparing fractions with both different numerators and denominators. Consider comparing 5/6 and 7/9. There are several approaches:
-
Find a common denominator: The least common multiple of 6 and 9 is 18. Convert both fractions to have a denominator of 18:
5/6 = (5 x 3) / (6 x 3) = 15/18 7/9 = (7 x 2) / (9 x 2) = 14/18
Since 15/18 > 14/18, we can conclude that 5/6 > 7/9.
-
Cross-multiplication: Another method involves cross-multiplying. Multiply the numerator of the first fraction by the denominator of the second, and vice-versa. Compare the resulting products:
5/6 and 7/9
(5 x 9) = 45 (7 x 6) = 42
Since 45 > 42, we conclude that 5/6 > 7/9.
-
Decimal Conversion: Convert both fractions to decimals and compare:
5/6 ≈ 0.833 7/9 ≈ 0.778
Since 0.833 > 0.778, we can conclude that 5/6 > 7/9.
Frequently Asked Questions (FAQ)
Q1: Why is finding a common denominator important when comparing fractions?
A1: Finding a common denominator allows us to express the fractions in a way that's directly comparable. It’s like converting different units of measurement (e.g., inches and centimeters) into the same unit before comparing them. Without a common denominator, it's difficult to directly compare the sizes of the fractions.
Q2: Is there a shortcut for comparing fractions?
A2: While there isn't a single universal shortcut, cross-multiplication offers a relatively quick method for comparing fractions with different numerators and denominators. Visual comparison can also be a quick way to get an approximate idea of the relative sizes of fractions.
Q3: What if the fractions are mixed numbers (e.g., 2 1/2)?
A3: To compare mixed numbers, you can either convert them into improper fractions (where the numerator is larger than the denominator) and then use the methods described above, or you can compare the whole number parts first and then the fractional parts if necessary.
Q4: Can I use a calculator to compare fractions?
A4: Yes, you can use a calculator to convert fractions to decimals, making comparison simpler. However, understanding the underlying principles of fraction comparison is essential for developing mathematical proficiency.
Q5: How can I improve my skills in comparing fractions?
A5: Practice is key! Regularly work through comparison problems, using different methods, and gradually increase the complexity of the fractions you compare. Visual aids like fraction circles or bars can be helpful, especially for beginners.
Conclusion: Mastering Fraction Comparison
The question, "Is 3/4 greater than 3/8?" serves as a springboard to explore the fundamental principles of fraction comparison. We've examined several methods, from visual representations to numerical calculations, providing a comprehensive understanding of this essential mathematical concept. Mastering fraction comparison is not only crucial for academic success but also invaluable in various real-world applications. By understanding the concepts of equivalent fractions and common denominators, you can confidently compare and manipulate fractions to solve problems and make informed decisions across various fields. Remember to practice regularly and use a combination of methods to solidify your understanding and improve your skills. With consistent effort, you will confidently navigate the world of fractions.
Latest Posts
Latest Posts
-
What Percent Is 1 10
Sep 18, 2025
-
What Is 5 6 Of 3 4
Sep 18, 2025
-
17 Percent As A Fraction
Sep 18, 2025
-
Numbers From Least To Greatest
Sep 18, 2025
-
690 Billion Nanograms To Pounds
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about Is 3/4 Greater Than 3/8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.