Is 3/4 More Than 1/2
saludintensiva
Sep 14, 2025 · 5 min read
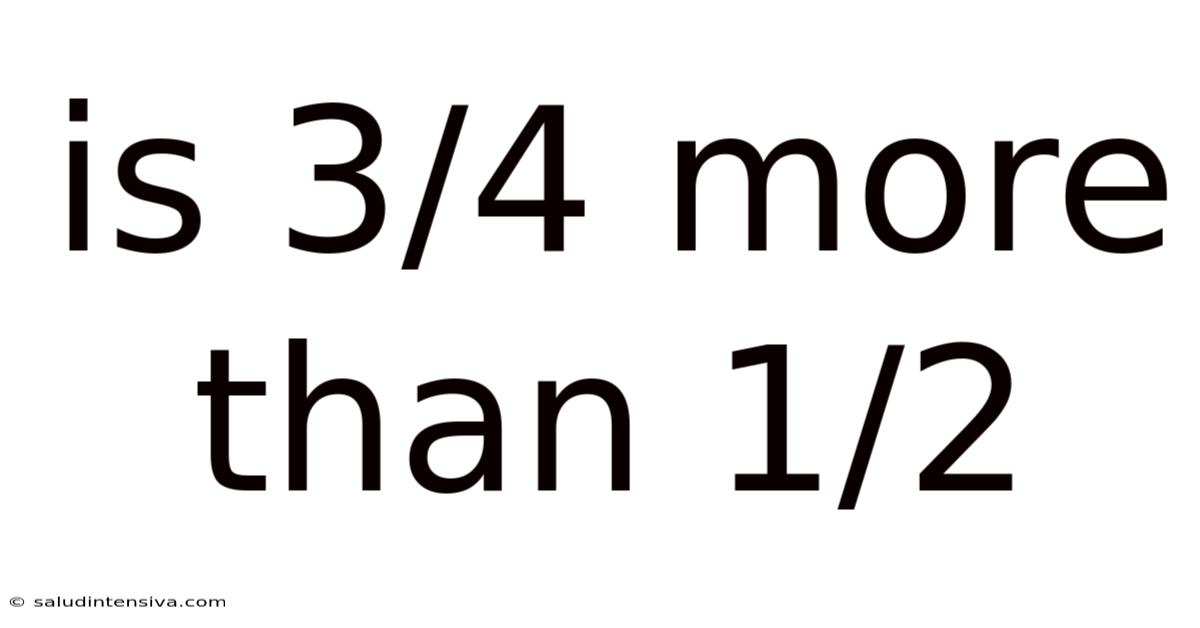
Table of Contents
Is 3/4 More Than 1/2? A Deep Dive into Fraction Comparison
Understanding fractions is a fundamental skill in mathematics, crucial for everyday life and advanced studies. One common question, especially for beginners, is whether 3/4 is more than 1/2. This article provides a comprehensive explanation, going beyond a simple "yes" or "no" to explore various methods for comparing fractions, their practical applications, and the underlying mathematical concepts. We'll also address frequently asked questions and delve into the importance of mastering fraction comparison.
Introduction: Understanding Fractions
Before we tackle the central question, let's refresh our understanding of fractions. A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). The denominator indicates how many equal parts the whole is divided into, while the numerator shows how many of those parts are being considered. For example, in the fraction 3/4, the denominator 4 means the whole is divided into four equal parts, and the numerator 3 indicates that we're considering three of those parts.
Method 1: Visual Comparison
The simplest way to compare 3/4 and 1/2 is through visual representation. Imagine two identical circles. Divide the first circle into four equal parts and shade three of them to represent 3/4. Divide the second circle into two equal parts and shade one to represent 1/2. By visually comparing the shaded areas, it's immediately clear that the shaded portion of the circle representing 3/4 is larger than the shaded portion representing 1/2. This visual method is particularly helpful for beginners as it provides an intuitive understanding of the concept.
Method 2: Finding a Common Denominator
A more formal approach involves finding a common denominator for both fractions. This means finding a number that is divisible by both the denominators of 3/4 and 1/2. In this case, the least common denominator (LCD) is 4. We convert 1/2 to an equivalent fraction with a denominator of 4 by multiplying both the numerator and the denominator by 2:
1/2 * 2/2 = 2/4
Now we can compare 3/4 and 2/4. Since 3 > 2, it's clear that 3/4 > 2/4, and therefore, 3/4 > 1/2. This method emphasizes the importance of equivalent fractions—fractions that represent the same value but have different numerators and denominators.
Method 3: Converting to Decimals
Another approach involves converting both fractions to decimals. To convert a fraction to a decimal, divide the numerator by the denominator.
3/4 = 3 ÷ 4 = 0.75
1/2 = 1 ÷ 2 = 0.5
Comparing the decimal values, we see that 0.75 > 0.5, confirming that 3/4 is greater than 1/2. This method is useful when working with calculations or comparisons that involve decimal numbers.
Method 4: Using Number Lines
A number line provides a visual representation of the relative positions of numbers. Plotting both 3/4 and 1/2 on a number line clearly shows that 3/4 lies to the right of 1/2, indicating that 3/4 is greater. This method reinforces the concept of number ordering and magnitude.
The Importance of Mastering Fraction Comparison
The ability to compare fractions is not just an academic exercise; it’s a crucial skill applicable in many real-world scenarios:
- Cooking and Baking: Following recipes often involves understanding fraction measurements (e.g., 1/2 cup, 3/4 teaspoon). Accurate comparisons are vital for achieving desired results.
- Construction and Engineering: Precision is paramount in these fields. Comparing fractions is essential for accurate measurements and calculations.
- Finance: Understanding fractions is crucial for comprehending percentages, interest rates, and proportions in financial calculations.
- Data Analysis: Representing and interpreting data frequently involves using fractions and percentages.
- Everyday Life: Numerous everyday situations, from dividing resources to understanding sales discounts, require a grasp of fraction comparison.
Beyond the Basics: Comparing More Complex Fractions
While the comparison of 3/4 and 1/2 is relatively straightforward, let's consider how these methods extend to more complex fractions. For example, consider comparing 5/8 and 2/3.
Using the common denominator method, we find the LCD of 8 and 3, which is 24. Then we convert both fractions:
5/8 * 3/3 = 15/24
2/3 * 8/8 = 16/24
Since 16/24 > 15/24, we conclude that 2/3 > 5/8.
Converting to decimals:
5/8 = 0.625
2/3 = 0.666... (a repeating decimal)
Again, we see that 2/3 > 5/8.
Frequently Asked Questions (FAQ)
Q: Are there other ways to compare fractions?
A: Yes, there are other techniques, such as cross-multiplication, which is particularly useful for comparing fractions with different denominators. In this method, you multiply the numerator of one fraction by the denominator of the other, and vice-versa. The fraction with the larger product is the larger fraction.
Q: What if the fractions have negative values?
A: When comparing negative fractions, the rules reverse. The fraction with the larger absolute value will be considered smaller (since it’s further to the left on the number line). For example, -3/4 is greater than -1/2.
Q: How can I help my child understand fraction comparison?
A: Use visual aids like diagrams and manipulatives (like fraction circles or blocks). Start with simple comparisons and gradually increase the complexity. Real-world examples and hands-on activities can significantly improve understanding.
Q: What resources are available for further learning about fractions?
A: Numerous online resources, educational websites, and textbooks offer comprehensive lessons and practice exercises on fractions.
Conclusion: Mastering Fraction Comparison for a Brighter Future
In conclusion, 3/4 is indeed more than 1/2. Understanding this fundamental comparison opens doors to a deeper comprehension of fractions and their diverse applications. This article explored multiple methods for comparing fractions, highlighting their versatility and practical significance. By mastering these methods and consistently practicing, you can build a solid foundation in mathematics and confidently tackle more complex fraction problems in various aspects of your life. Remember, the key to success lies in understanding the underlying concepts and selecting the most suitable method for each situation. With consistent practice and a willingness to explore different approaches, the world of fractions will become increasingly accessible and rewarding.
Latest Posts
Latest Posts
-
13 15 As A Percentage
Sep 14, 2025
-
Gcf Of 100 And 30
Sep 14, 2025
-
What Time Is 17 39
Sep 14, 2025
-
Gcf Of 8 And 4
Sep 14, 2025
-
Gcf Of 56 And 64
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about Is 3/4 More Than 1/2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.