Is 3/8 Smaller Than 1/2
saludintensiva
Sep 13, 2025 · 6 min read
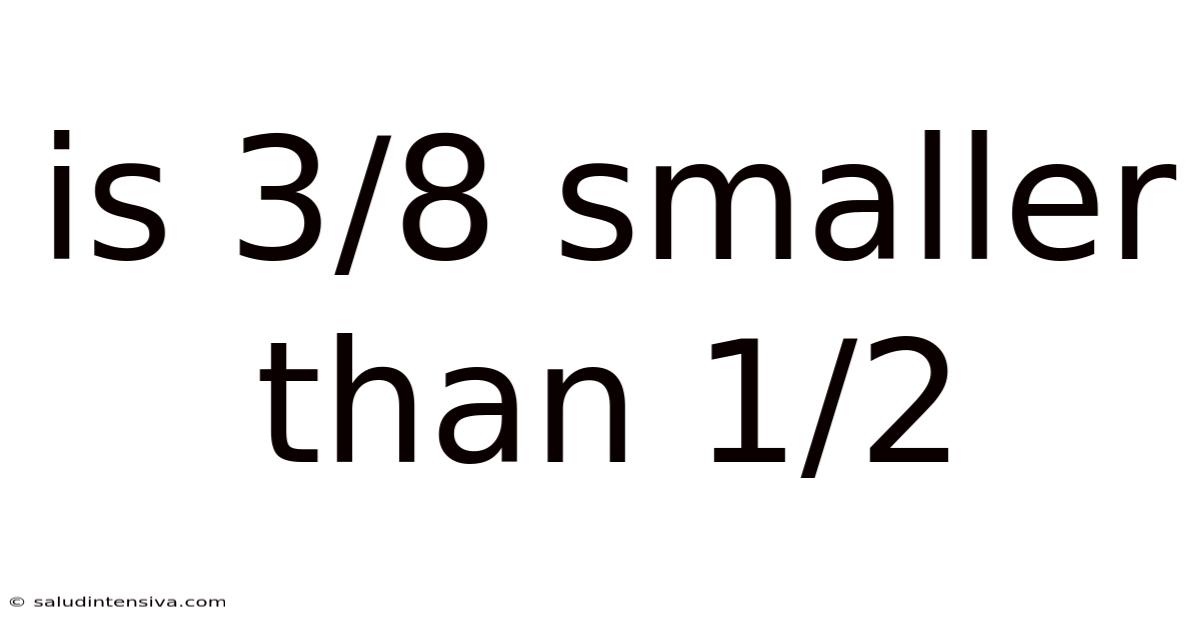
Table of Contents
Is 3/8 Smaller Than 1/2? A Deep Dive into Fraction Comparison
Understanding fractions is a fundamental skill in mathematics, crucial for everything from baking a cake to calculating complex engineering designs. A common question that arises, especially for those beginning their journey with fractions, is: is 3/8 smaller than 1/2? This article will not only answer that question definitively but will also explore the various methods for comparing fractions, providing a comprehensive understanding of this essential mathematical concept. We will delve into the underlying principles, offer practical examples, and address frequently asked questions to ensure a thorough grasp of the topic.
Introduction: Understanding Fractions
Before tackling the core question, let's refresh our understanding of fractions. A fraction represents a part of a whole. It's composed of two key parts:
- Numerator: The top number, indicating the number of parts we have.
- Denominator: The bottom number, indicating the total number of equal parts the whole is divided into.
For example, in the fraction 3/8, the numerator is 3 (we have 3 parts) and the denominator is 8 (the whole is divided into 8 equal parts).
Method 1: Finding a Common Denominator
The most straightforward method for comparing fractions is to find a common denominator. This involves converting both fractions so they share the same denominator. Once they have the same denominator, we can simply compare the numerators.
Let's apply this to our question: Is 3/8 smaller than 1/2?
First, we need to find a common denominator for 8 and 2. The least common multiple (LCM) of 8 and 2 is 8.
Now, let's convert 1/2 to an equivalent fraction with a denominator of 8:
To change the denominator from 2 to 8, we multiply it by 4. To maintain the value of the fraction, we must also multiply the numerator by 4:
(1 * 4) / (2 * 4) = 4/8
Now we can compare 3/8 and 4/8:
Since 3 < 4, we conclude that 3/8 < 4/8. Therefore, 3/8 is smaller than 1/2.
Method 2: Converting to Decimals
Another effective method for comparing fractions is to convert them to decimals. This involves dividing the numerator by the denominator for each fraction.
Let's convert 3/8 and 1/2 to decimals:
3 ÷ 8 = 0.375
1 ÷ 2 = 0.5
Now we can easily compare the decimal values:
Since 0.375 < 0.5, we again conclude that 3/8 is smaller than 1/2.
Method 3: Visual Representation
Visualizing fractions can be incredibly helpful, especially for beginners. Imagine a circle divided into 8 equal parts. Shading 3 of these parts represents 3/8. Now, imagine another circle divided into 2 equal parts. Shading one part represents 1/2. By visually comparing the shaded areas, it's clear that the shaded area representing 3/8 is smaller than the shaded area representing 1/2. This visual method reinforces the understanding that 3/8 is smaller than 1/2.
Method 4: Using Benchmark Fractions
Benchmark fractions, such as 0, 1/2, and 1, provide excellent reference points for comparing fractions. We can use these benchmarks to estimate the size of a fraction.
1/2 is exactly halfway between 0 and 1. 3/8 is less than halfway between 0 and 1, while 1/2 is exactly halfway. Therefore, 3/8 is smaller than 1/2.
A Deeper Look: Understanding Fraction Magnitude
Comparing fractions isn't just about applying methods; it's about understanding the underlying relationship between the numerator and the denominator. A larger numerator relative to the denominator indicates a larger fraction. Conversely, a smaller numerator relative to the denominator indicates a smaller fraction.
In 3/8, the numerator (3) is significantly smaller than the denominator (8), indicating a relatively small fraction. In 1/2, the numerator (1) is half of the denominator (2), indicating a fraction that represents exactly half of the whole.
Practical Applications: Real-World Examples
The ability to compare fractions is essential in numerous real-world scenarios. Consider these examples:
- Baking: A recipe calls for 1/2 cup of sugar and you only have 3/8 cup. You'll need more sugar.
- Construction: Measuring materials accurately requires understanding fraction comparisons to ensure correct measurements.
- Data Analysis: Interpreting data represented as fractions necessitates accurate comparisons.
- Finance: Calculating proportions and percentages often involves working with fractions.
Frequently Asked Questions (FAQ)
Q: Are there other methods to compare fractions besides these?
A: Yes, there are other techniques, including cross-multiplication, which involves multiplying the numerator of one fraction by the denominator of the other and vice versa. However, the methods outlined above are generally considered the most intuitive and accessible for a wide range of learners.
Q: What if the denominators are not easily related, like comparing 5/12 and 7/18?
A: In such cases, finding the least common multiple (LCM) of the denominators becomes crucial. The LCM of 12 and 18 is 36. Convert both fractions to equivalent fractions with a denominator of 36 and compare the numerators.
Q: Why is finding a common denominator important?
A: Finding a common denominator allows us to directly compare the sizes of the fractions by comparing their numerators. Without a common denominator, the denominators represent different-sized parts of the whole, making direct comparison impossible.
Q: Is there a shortcut to determine if a fraction is greater than or less than 1/2?
A: Yes, if you double the numerator and compare it to the denominator, it can be a quick way to assess its relationship to 1/2. If double the numerator is less than the denominator, the fraction is less than 1/2. If it's greater than the denominator, the fraction is greater than 1/2. If it equals the denominator, the fraction equals 1/2.
Conclusion: Mastering Fraction Comparison
Comparing fractions is a vital skill in mathematics. This article has demonstrated several methods to effectively determine whether one fraction is larger or smaller than another, using the example of 3/8 and 1/2. By understanding these methods—finding a common denominator, converting to decimals, visual representation, and using benchmark fractions—you'll develop confidence and proficiency in working with fractions. Remember to practice regularly, applying these methods to various fraction comparison problems. With consistent effort, you'll master this essential mathematical concept and confidently navigate countless real-world situations that involve fractions. The key is to understand the underlying principles and choose the method that best suits your understanding and the specific problem at hand. So, keep practicing, and you'll become a fraction comparison expert in no time!
Latest Posts
Latest Posts
-
1600 Hours In Military Time
Sep 13, 2025
-
List Of Multiples Of 7
Sep 13, 2025
-
2 3 Of 1 3
Sep 13, 2025
-
How Long Is 14000 Hours
Sep 13, 2025
-
5 Out Of 15 Percentage
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about Is 3/8 Smaller Than 1/2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.