Is 5/8 Greater Than 5/6
saludintensiva
Sep 10, 2025 · 6 min read
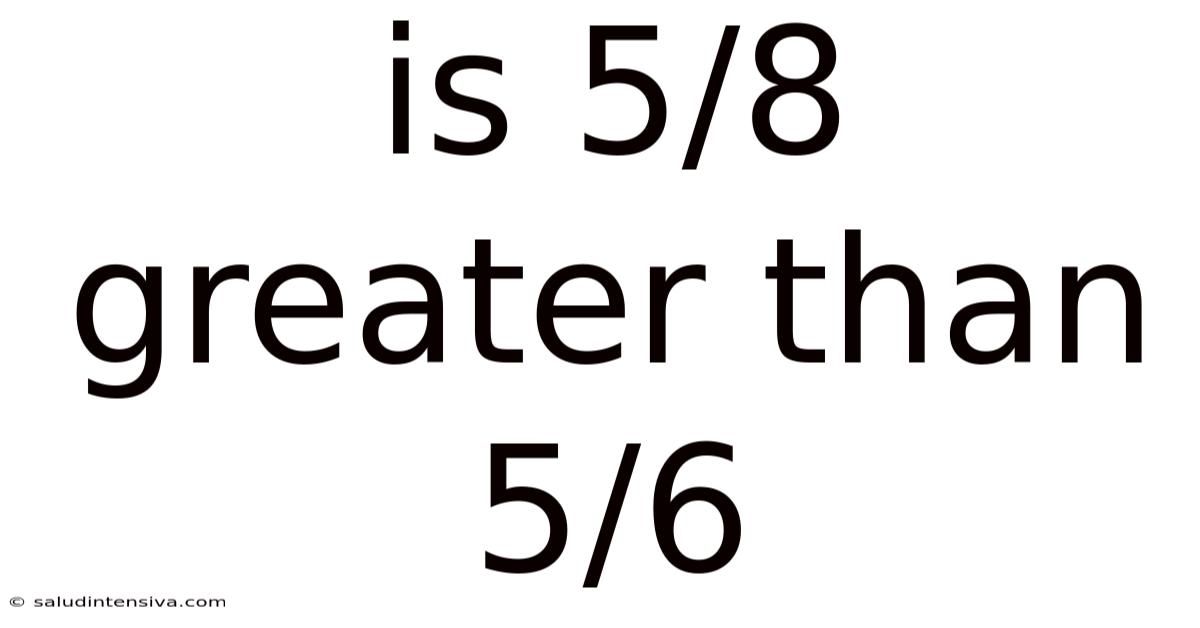
Table of Contents
Is 5/8 Greater Than 5/6? Understanding Fraction Comparison
Understanding fractions is a fundamental skill in mathematics, crucial for various applications in everyday life and advanced studies. A common question that arises, especially for beginners, is comparing the relative sizes of fractions. This article delves into the question: "Is 5/8 greater than 5/6?" We will not only answer this directly but also explore various methods for comparing fractions, providing you with a comprehensive understanding of this essential mathematical concept. This will equip you with the tools to confidently compare any two fractions.
Introduction: Deciphering the Language of Fractions
Before diving into the comparison, let's refresh our understanding of fractions. A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). The denominator indicates the total number of equal parts the whole is divided into, while the numerator represents the number of those parts being considered.
In our case, we're comparing 5/8 and 5/6. 5/8 means we're considering 5 out of 8 equal parts of a whole, while 5/6 means we're considering 5 out of 6 equal parts of a whole. The crucial point here is that the whole is divided into different numbers of parts in each fraction. This is what makes the comparison slightly more complex than simply comparing the numerators.
Method 1: Visual Comparison – The Power of Pictorial Representation
One of the most intuitive ways to compare fractions, especially for beginners, is through visual representation. Imagine two identical circles.
-
Circle 1: Divide this circle into 8 equal slices (representing the denominator of 5/8). Shade in 5 of those slices (representing the numerator).
-
Circle 2: Divide this circle into 6 equal slices (representing the denominator of 5/6). Shade in 5 of those slices (representing the numerator).
By visually comparing the shaded areas, you can intuitively see that a larger portion of the second circle (5/6) is shaded compared to the first circle (5/8). Therefore, 5/6 is greater than 5/8. This visual method helps build an intuitive understanding of fraction comparison, making the concept less abstract.
Method 2: Finding a Common Denominator – The Bedrock of Fraction Comparison
While visual comparison is helpful, it's not always practical for larger or more complex fractions. A more robust and universally applicable method is finding a common denominator. This involves transforming both fractions so they share the same denominator, allowing for a direct comparison of their numerators.
To find a common denominator for 5/8 and 5/6, we need to find the least common multiple (LCM) of 8 and 6. The multiples of 8 are 8, 16, 24, 32... and the multiples of 6 are 6, 12, 18, 24, 30... The smallest number that appears in both lists is 24. This will be our common denominator.
Now, we convert each fraction to an equivalent fraction with a denominator of 24:
-
5/8: To change the denominator from 8 to 24, we multiply both the numerator and the denominator by 3 (because 24/8 = 3): (5 x 3) / (8 x 3) = 15/24
-
5/6: To change the denominator from 6 to 24, we multiply both the numerator and the denominator by 4 (because 24/6 = 4): (5 x 4) / (6 x 4) = 20/24
Now that both fractions have the same denominator, we can directly compare their numerators. Since 20 > 15, we can conclude that 20/24 (or 5/6) is greater than 15/24 (or 5/8).
Method 3: Converting to Decimals – A Numerical Approach
Another effective way to compare fractions is by converting them to decimals. This method is particularly useful when dealing with fractions that are difficult to visualize or find a common denominator for.
To convert a fraction to a decimal, simply divide the numerator by the denominator:
-
5/8 = 0.625
-
5/6 = 0.8333... (this is a repeating decimal)
Comparing the decimal values, it's clear that 0.8333... is greater than 0.625. Therefore, 5/6 is greater than 5/8.
Method 4: Cross-Multiplication – A Quick Comparison Technique
Cross-multiplication provides a quick way to compare two fractions. This method is particularly efficient when dealing with fractions that don't easily share a common denominator.
To compare 5/8 and 5/6 using cross-multiplication:
-
Multiply the numerator of the first fraction (5) by the denominator of the second fraction (6): 5 x 6 = 30
-
Multiply the numerator of the second fraction (5) by the denominator of the first fraction (8): 5 x 8 = 40
-
Compare the results: Since 30 < 40, the fraction with the smaller result (5/8) is smaller than the fraction with the larger result (5/6).
Understanding the Logic Behind the Comparison
The reason 5/6 is greater than 5/8 boils down to the size of the pieces representing the whole. When the whole is divided into fewer parts (as in 5/6), each part is larger. Even though we're considering 5 parts in both cases, the larger individual parts in 5/6 result in a larger overall fraction. This concept underscores the importance of considering both the numerator and the denominator when comparing fractions.
Expanding the Understanding: Comparing Fractions with Different Numerators and Denominators
The methods described above are applicable to comparing any two fractions, even those with different numerators and denominators. For instance, let's compare 7/12 and 2/3.
Using the common denominator method:
-
The LCM of 12 and 3 is 12.
-
2/3 = (2 x 4) / (3 x 4) = 8/12
-
Comparing 7/12 and 8/12, we see that 8/12 > 7/12, therefore 2/3 > 7/12.
This demonstrates the flexibility and power of these comparison methods.
Frequently Asked Questions (FAQs)
-
Q: Is there a quick way to tell if one fraction is bigger than another without performing calculations? A: Not always. While sometimes you can visually estimate, generally, methods like finding a common denominator or cross-multiplication are needed for accurate comparison.
-
Q: What if the fractions are negative? A: The comparison methods remain the same, but remember that with negative fractions, the fraction with the larger absolute value is actually smaller. For instance, -1/2 is greater than -2/3 because -0.5 > -0.666...
-
Q: Can I use a calculator to compare fractions? A: Yes! Convert the fractions to decimals using a calculator and compare the decimal values.
-
Q: Are there any other methods for comparing fractions? A: Yes, there are more advanced techniques used in higher-level mathematics. However, the methods discussed here are sufficient for most practical purposes.
Conclusion: Mastering Fraction Comparison
Comparing fractions is a fundamental skill that builds the foundation for more advanced mathematical concepts. While the question "Is 5/8 greater than 5/6?" might seem simple at first glance, it provides a stepping stone to understanding the nuances of fraction comparison. We've explored several methods – visual representation, finding a common denominator, converting to decimals, and cross-multiplication – each offering a unique approach to solving this type of problem. Mastering these methods empowers you to confidently compare any two fractions, strengthening your mathematical abilities and opening doors to more complex mathematical explorations. Remember to choose the method that best suits your understanding and the complexity of the fractions you are comparing. Practice makes perfect!
Latest Posts
Latest Posts
-
100 3 Degrees Fahrenheit To Celsius
Sep 10, 2025
-
What Is 0 4 In Percentage
Sep 10, 2025
-
4th Square Root Of 81
Sep 10, 2025
-
Rounding To Nearest Hundred Thousand
Sep 10, 2025
-
How Big Is 6 Meters
Sep 10, 2025
Related Post
Thank you for visiting our website which covers about Is 5/8 Greater Than 5/6 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.