Is 7/12 Greater Than 1/2
saludintensiva
Sep 10, 2025 · 5 min read
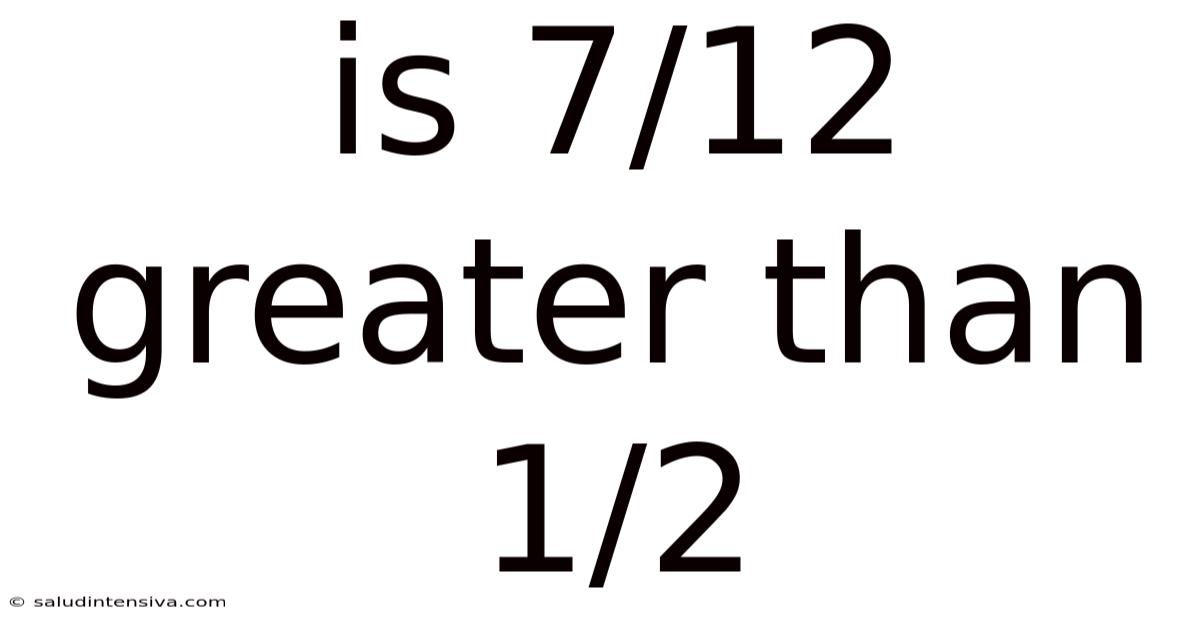
Table of Contents
Is 7/12 Greater Than 1/2? A Deep Dive into Fraction Comparison
Is 7/12 greater than 1/2? This seemingly simple question opens the door to a deeper understanding of fractions, a fundamental concept in mathematics crucial for various applications in everyday life and advanced studies. This comprehensive guide will not only answer this question definitively but also equip you with the tools and knowledge to confidently compare any two fractions. We'll explore various methods, from visual representations to numerical calculations, ensuring a thorough grasp of the underlying principles.
Introduction: Understanding Fractions
Before we tackle the central question, let's refresh our understanding of fractions. A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). The denominator indicates the total number of equal parts the whole is divided into, while the numerator indicates how many of those parts are being considered. For example, in the fraction 1/2, the denominator (2) shows the whole is divided into two equal parts, and the numerator (1) indicates we're considering one of those parts – half of the whole.
Method 1: Visual Comparison
One of the most intuitive ways to compare fractions is through visual representation. Imagine a pizza cut into 12 slices (representing the denominator of 7/12). 7/12 means you have 7 out of those 12 slices. Now, imagine another pizza cut into 2 slices (representing the denominator of 1/2). 1/2 means you have 1 out of those 2 slices. Which pizza gives you more?
To make the comparison easier, let's divide the second pizza (1/2) into smaller, equal slices that match the size of the slices in the first pizza (7/12). Since 1/2 is equivalent to 6/12 (we multiplied both numerator and denominator by 6), we can clearly see that 7/12 (7 slices) is greater than 6/12 (6 slices). Therefore, 7/12 is greater than 1/2.
Method 2: Finding a Common Denominator
A more formal approach involves finding a common denominator for both fractions. The common denominator is a number that is a multiple of both denominators. In this case, the denominators are 12 and 2. The least common multiple (LCM) of 12 and 2 is 12.
- We don't need to change 7/12, as its denominator is already 12.
- To convert 1/2 to an equivalent fraction with a denominator of 12, we multiply both the numerator and the denominator by 6: (1 * 6) / (2 * 6) = 6/12.
Now we compare 7/12 and 6/12. Since 7 > 6, we can conclude that 7/12 > 6/12, which means 7/12 > 1/2.
Method 3: Converting to Decimals
Another effective method is converting both fractions to decimals. This involves dividing the numerator by the denominator.
- 7/12 = 0.58333...
- 1/2 = 0.5
By comparing the decimal values, we see that 0.58333... > 0.5, confirming that 7/12 is greater than 1/2.
Method 4: Cross-Multiplication
Cross-multiplication provides a quick and efficient method for comparing fractions. To compare a/b and c/d, we cross-multiply: a * d and b * c.
- For 7/12 and 1/2, we have:
- 7 * 2 = 14
- 12 * 1 = 12
Since 14 > 12, we conclude that 7/12 > 1/2. If the result of the cross-multiplication were equal, the fractions would be equivalent. If the inequality were reversed, the first fraction would be smaller than the second.
Explanation with Number Lines
Visualizing fractions on a number line can enhance understanding. A number line represents numbers sequentially. We can mark 0, 1, and fractions between them. Plotting 7/12 and 1/2 on the number line shows that 7/12 is positioned to the right of 1/2, indicating that 7/12 is greater. This method, though less precise for very close fractions, provides an excellent visual confirmation of the comparison.
A Deeper Dive into Fraction Comparison Techniques
The methods above provide solid groundwork for comparing fractions. Let's delve deeper into some nuances and advanced techniques:
-
Improper Fractions and Mixed Numbers: If you encounter improper fractions (where the numerator is greater than or equal to the denominator) or mixed numbers (a combination of a whole number and a fraction), convert them to improper fractions before applying any comparison method. For instance, comparing 1 1/4 and 7/12 requires converting 1 1/4 to 5/4 before comparison.
-
Simplifying Fractions: Simplifying fractions to their lowest terms before comparison can make calculations easier. For example, simplifying 6/12 to 1/2 streamlines the comparison process.
-
Estimating: For a quick estimate, especially when dealing with larger numbers, consider rounding or approximating the fractions. This won't give an exact answer, but it can provide a reasonable guess.
-
Using a Calculator: Calculators can be particularly helpful for complex fractions or when converting fractions to decimals. However, understanding the underlying principles remains crucial for comprehension and problem-solving.
Frequently Asked Questions (FAQ)
-
Q: What if the denominators are significantly different? A: Finding the least common multiple (LCM) might be time-consuming. In such cases, converting to decimals or cross-multiplication are often more efficient.
-
Q: Can I compare fractions using only their numerators? A: No, comparing only numerators is only valid if the denominators are the same. Different denominators represent different sized parts of a whole.
-
Q: Are there any tricks for quickly comparing fractions? A: Practice makes perfect! Familiarity with common fractions and their decimal equivalents speeds up the process. Cross-multiplication is a fast method for many comparisons.
-
Q: Why is understanding fraction comparison important? A: Fraction comparison forms the foundation for numerous mathematical concepts and real-world applications, including measurement, ratios, proportions, and advanced algebra.
Conclusion: Mastering Fraction Comparison
Determining whether 7/12 is greater than 1/2 is not merely about finding the answer; it’s about grasping the core concepts of fraction comparison. Through visual representations, finding common denominators, decimal conversions, and cross-multiplication, we've definitively established that 7/12 is greater than 1/2. Mastering these methods empowers you to confidently compare any pair of fractions, paving the way for a more profound understanding of mathematical principles and their practical applications in various fields. Remember that consistent practice and understanding the underlying logic are key to developing fluency in fraction comparison. This seemingly small skill contributes significantly to your overall mathematical proficiency. Keep practicing, and you'll find yourself effortlessly navigating the world of fractions!
Latest Posts
Latest Posts
-
4 3 8 As A Decimal
Sep 10, 2025
-
How To Simplify Negative Fractions
Sep 10, 2025
-
5 To The 4th Power
Sep 10, 2025
-
1 15 Random Number Generator
Sep 10, 2025
-
Lcm For 8 And 3
Sep 10, 2025
Related Post
Thank you for visiting our website which covers about Is 7/12 Greater Than 1/2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.