Lcm For 8 And 3
saludintensiva
Sep 10, 2025 · 6 min read
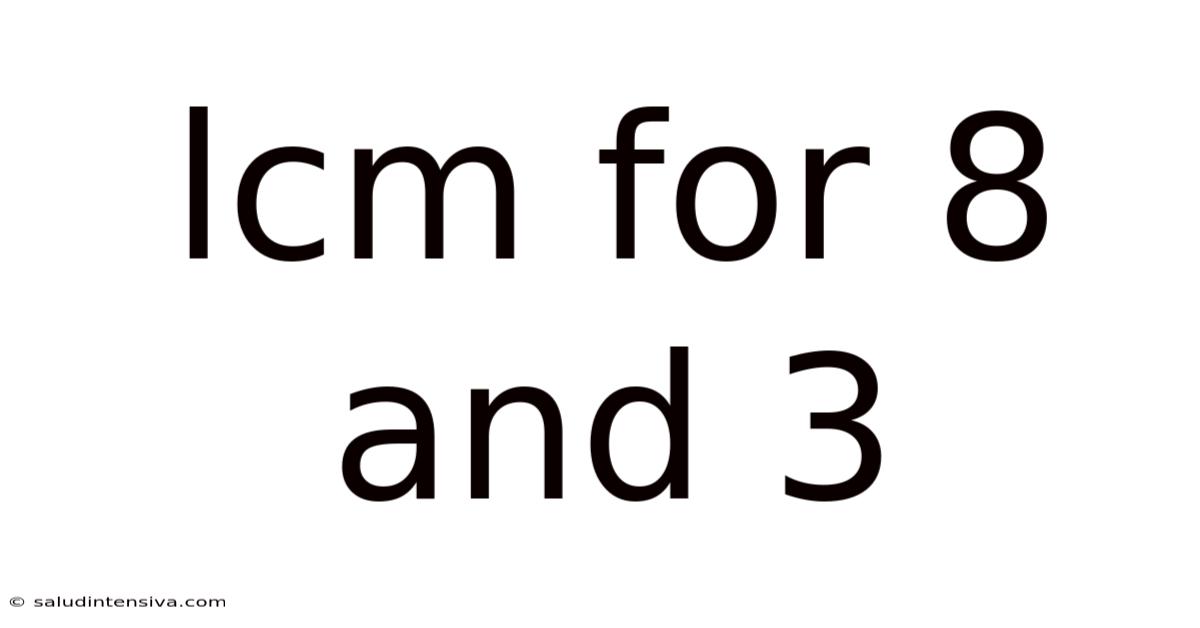
Table of Contents
Finding the Least Common Multiple (LCM) of 8 and 3: A Deep Dive
Finding the least common multiple (LCM) of two numbers might seem like a simple arithmetic task, but understanding the underlying concepts and different methods provides a strong foundation in number theory and has practical applications in various fields, from scheduling to music theory. This article will delve into the process of finding the LCM of 8 and 3, exploring various methods and explaining the mathematical principles involved. We'll cover the basic concepts, multiple approaches to finding the LCM, and even explore the theoretical underpinnings to enhance your understanding beyond a simple calculation.
Understanding Least Common Multiples (LCM)
Before we jump into calculating the LCM of 8 and 3, let's define what a least common multiple actually is. The LCM of two or more integers is the smallest positive integer that is divisible by all the integers. In simpler terms, it's the smallest number that contains all the numbers as factors. For example, the multiples of 8 are 8, 16, 24, 32, 40, 48, … and the multiples of 3 are 3, 6, 9, 12, 15, 18, 21, 24, … Notice that 24 is the smallest number that appears in both lists; therefore, 24 is the LCM of 8 and 3.
This concept extends to more than two numbers. Finding the LCM of several numbers involves identifying the smallest positive integer that is a multiple of all the numbers involved. Understanding LCMs is crucial in various contexts. For instance, consider scheduling tasks that repeat at different intervals. If Task A repeats every 8 days and Task B every 3 days, the LCM will tell you when both tasks will coincide again.
Methods for Finding the LCM of 8 and 3
There are several effective methods for determining the LCM of two numbers, and we'll explore the most common ones, applying them to our example of 8 and 3.
1. Listing Multiples:
This is the most straightforward approach, especially for smaller numbers. We list the multiples of each number until we find the smallest common multiple.
- Multiples of 8: 8, 16, 24, 32, 40, ...
- Multiples of 3: 3, 6, 9, 12, 15, 18, 21, 24, ...
As we can see, the smallest number that appears in both lists is 24. Therefore, the LCM of 8 and 3 is 24. This method is simple and intuitive, but it can become tedious with larger numbers.
2. Prime Factorization Method:
This method is more efficient, especially for larger numbers. It involves finding the prime factorization of each number and then constructing the LCM using the highest powers of all prime factors present.
- Prime factorization of 8: 2³ (8 = 2 x 2 x 2)
- Prime factorization of 3: 3¹ (3 is a prime number)
To find the LCM, we take the highest power of each prime factor present in either factorization:
- Highest power of 2: 2³ = 8
- Highest power of 3: 3¹ = 3
Multiply these together: 8 x 3 = 24. Therefore, the LCM of 8 and 3 is 24. This method is more systematic and less prone to errors, making it preferable for larger numbers.
3. Using the Greatest Common Divisor (GCD):
There's a crucial relationship between the LCM and the greatest common divisor (GCD) of two numbers. The GCD is the largest number that divides both numbers without leaving a remainder. The formula connecting LCM and GCD is:
LCM(a, b) = (|a * b|) / GCD(a, b)
where |a * b| represents the absolute value of the product of a and b.
Let's apply this to 8 and 3:
- First, we find the GCD of 8 and 3. The only positive integer that divides both 8 and 3 is 1. Therefore, GCD(8, 3) = 1.
- Now, we use the formula: LCM(8, 3) = (8 * 3) / 1 = 24
This method is efficient when you already know the GCD or can easily calculate it using methods like the Euclidean algorithm (explained below).
4. Euclidean Algorithm for GCD:
The Euclidean algorithm is a highly efficient method for finding the greatest common divisor (GCD) of two numbers. It's particularly useful for larger numbers where listing factors becomes impractical. The algorithm works iteratively by repeatedly applying the division algorithm until the remainder is 0. The last non-zero remainder is the GCD.
Let's find the GCD of 8 and 3 using the Euclidean algorithm:
- Divide the larger number (8) by the smaller number (3): 8 = 2 * 3 + 2
- Replace the larger number with the smaller number (3) and the smaller number with the remainder (2): 3 = 1 * 2 + 1
- Repeat: 2 = 2 * 1 + 0
The last non-zero remainder is 1, so GCD(8, 3) = 1. As shown in the previous method, we can then use this GCD to calculate the LCM.
Why is Understanding LCM Important?
The concept of LCM extends beyond simple arithmetic exercises. It has significant applications in diverse fields:
-
Scheduling: As mentioned earlier, LCM helps determine when cyclical events coincide. This is useful in scheduling tasks, appointments, or production cycles.
-
Music Theory: LCM is essential in understanding musical intervals and harmonies. The LCM of the frequencies of two notes determines when they will be in phase, creating a harmonious sound.
-
Construction and Engineering: LCM finds applications in projects requiring precise alignment or synchronization of repetitive elements, such as building structures or designing machinery.
-
Computer Science: In algorithms and data structures, the concept of LCM helps optimize processes and improve efficiency.
Frequently Asked Questions (FAQ)
Q: Is the LCM always greater than the two numbers?
A: Yes, if the two numbers are greater than 1, their LCM will always be greater than or equal to the larger of the two numbers. If one of the numbers is 1, the LCM will be the other number.
Q: What if I have more than two numbers? How do I find their LCM?
A: You can extend the prime factorization method or the GCD-based method to accommodate more than two numbers. For prime factorization, find the prime factorization of each number and take the highest power of each prime factor present. For the GCD method, you would need to calculate the GCD of all numbers first and then apply the formula accordingly. This can become more complex with more numbers.
Q: Are there any online tools or calculators for finding LCM?
A: Yes, many online calculators are available that can compute the LCM of two or more numbers quickly. However, understanding the underlying methods is crucial for deeper comprehension and problem-solving.
Conclusion
Finding the LCM of 8 and 3, while seemingly straightforward, provides a valuable opportunity to explore fundamental concepts in number theory. The various methods presented—listing multiples, prime factorization, and the GCD-based approach—offer different perspectives and varying levels of efficiency, depending on the context and the size of the numbers involved. The deep understanding of LCM transcends simple calculation; its application extends to practical problem-solving in various domains, highlighting its importance in mathematics and beyond. The ability to calculate and understand LCM is a foundational skill in mathematics and an asset in diverse fields. Mastering this concept empowers you to tackle more complex mathematical challenges and to effectively solve problems in real-world scenarios.
Latest Posts
Latest Posts
-
30 Days From May 16th
Sep 10, 2025
-
What Is 3 4 In Half
Sep 10, 2025
-
Find The Height Of Cylinder
Sep 10, 2025
-
Gcf Of 14 And 18
Sep 10, 2025
-
Greatest Common Factor Of 14
Sep 10, 2025
Related Post
Thank you for visiting our website which covers about Lcm For 8 And 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.