Is 7/16 Bigger Than 1/2
saludintensiva
Sep 12, 2025 · 6 min read
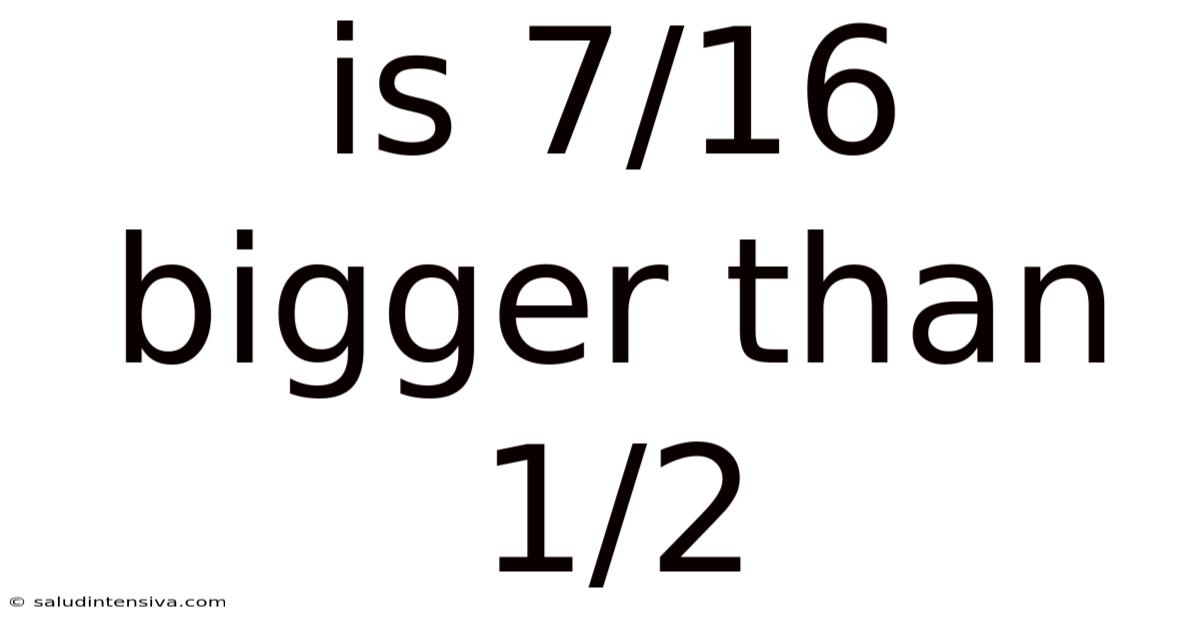
Table of Contents
Is 7/16 Bigger Than 1/2? A Deep Dive into Fraction Comparison
Are you struggling to compare fractions? Understanding whether 7/16 is bigger than 1/2 might seem simple at first glance, but it touches on fundamental concepts in mathematics crucial for various applications. This article will not only answer the question definitively but also equip you with the tools to compare any two fractions confidently. We'll explore different methods, delve into the underlying mathematical principles, and provide practical examples to solidify your understanding. Let's get started!
Understanding Fractions: A Quick Recap
Before we tackle the specific comparison, let's refresh our understanding of fractions. A fraction represents a part of a whole. It's written as a numerator (the top number) over a denominator (the bottom number), like this: a/b, where 'a' is the numerator and 'b' is the denominator. The denominator tells us how many equal parts the whole is divided into, and the numerator tells us how many of those parts we have.
For instance, 1/2 represents one out of two equal parts, or one-half. Similarly, 7/16 represents seven out of sixteen equal parts.
Method 1: Finding a Common Denominator
The most straightforward method for comparing fractions is to find a common denominator. This involves converting both fractions so they share the same denominator. Once they have the same denominator, we can easily compare their numerators.
To find a common denominator for 7/16 and 1/2, we need to find a number that is a multiple of both 16 and 2. The simplest common denominator is 16 because 2 x 8 = 16.
- Converting 1/2: To convert 1/2 to have a denominator of 16, we multiply both the numerator and the denominator by 8: (1 x 8) / (2 x 8) = 8/16
Now we can compare:
- 7/16 vs. 8/16
Since 7 is less than 8, we can conclude that 7/16 is smaller than 8/16, and therefore 7/16 is smaller than 1/2.
Method 2: Converting to Decimals
Another effective method is converting the fractions to decimals. This allows for a direct numerical comparison.
-
Converting 7/16 to a decimal: 7 ÷ 16 = 0.4375
-
Converting 1/2 to a decimal: 1 ÷ 2 = 0.5
Comparing the decimal values, we see that 0.4375 is less than 0.5. Therefore, 7/16 is smaller than 1/2.
Method 3: Visual Representation
Visualizing fractions can be particularly helpful for beginners. Imagine a pizza cut into 16 equal slices. 7/16 would represent seven of those slices. Now imagine another pizza cut into only two equal halves. 1/2 would represent one of those two halves. It’s intuitively clear that one half of a pizza is larger than seven-sixteenths of a pizza.
This visual approach reinforces the understanding of what fractions represent and makes the comparison more intuitive. You can use similar visual representations with other shapes or objects to compare fractions.
Method 4: Using Cross-Multiplication
Cross-multiplication provides a quick way to compare two fractions without finding a common denominator. To compare a/b and c/d, we cross-multiply:
- a x d and b x c
If a x d > b x c, then a/b > c/d. If a x d < b x c, then a/b < c/d.
Let's apply this to 7/16 and 1/2:
-
7 x 2 = 14
-
16 x 1 = 16
Since 14 < 16, we conclude that 7/16 < 1/2.
Why Understanding Fraction Comparison is Important
The ability to compare fractions is a fundamental skill in mathematics, with broad applications across various fields:
-
Everyday Life: From cooking (measuring ingredients) to budgeting (managing finances), fraction comparison helps in making accurate estimations and calculations.
-
Science and Engineering: In fields like physics and engineering, precise measurements and calculations involving fractions are crucial for designing structures, conducting experiments, and analyzing data.
-
Data Analysis: Interpreting data often involves working with fractions and percentages, requiring a strong understanding of fraction comparison for drawing meaningful conclusions.
Beyond the Basics: Exploring Equivalent Fractions
Equivalent fractions represent the same value even though they look different. For instance, 1/2, 2/4, 4/8, and 8/16 are all equivalent fractions. Understanding equivalent fractions is essential for simplifying fractions and comparing them effectively. To find equivalent fractions, you multiply or divide both the numerator and denominator by the same number (except zero).
Dealing with Mixed Numbers
Mixed numbers combine a whole number and a fraction (e.g., 1 1/2). To compare mixed numbers, you can either convert them into improper fractions (where the numerator is larger than the denominator) or compare the whole number parts first and then the fractional parts if the whole numbers are equal.
Frequently Asked Questions (FAQ)
Q: Are there any other methods for comparing fractions?
A: Yes, you can use a number line to visually compare fractions. Plot both fractions on the number line and see which one is further to the right (indicating a larger value).
Q: What if the denominators are very large and finding a common denominator is difficult?
A: In such cases, converting to decimals or using cross-multiplication is often a more efficient approach.
Q: How can I improve my understanding of fractions?
A: Practice is key! Solve various problems involving fractions, use visual aids, and work through different methods to reinforce your understanding. Online resources and educational materials can provide additional support.
Q: Why is it important to learn about common denominators?
A: A common denominator allows for a direct comparison of the numerators, simplifying the comparison process. It is the foundation for adding and subtracting fractions.
Q: Can I use a calculator to compare fractions?
A: While calculators can convert fractions to decimals, understanding the underlying mathematical principles is crucial for building a strong foundation in mathematics. Using a calculator without understanding the concept defeats the purpose of learning the skill.
Conclusion: Mastering Fraction Comparison
Comparing fractions, as illustrated by the example of 7/16 and 1/2, is a fundamental mathematical skill with wide-ranging applications. By understanding the different methods—finding a common denominator, converting to decimals, using cross-multiplication, and visual representation—you gain a powerful toolkit for tackling fraction comparisons with confidence. Remember, the key to mastering fractions lies in consistent practice and a thorough understanding of the underlying concepts. Don’t be afraid to explore different methods and find the one that works best for you. With practice and patience, you will become proficient in comparing fractions and appreciate their significance in various aspects of life and learning.
Latest Posts
Latest Posts
-
3 5 Is Equal To What
Sep 12, 2025
-
Lcm Of 6 And 18
Sep 12, 2025
-
Sum Of The Years Depreciation
Sep 12, 2025
-
1 6 2 In Fraction
Sep 12, 2025
-
1 65 As A Percent
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about Is 7/16 Bigger Than 1/2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.