1 65 As A Percent
saludintensiva
Sep 12, 2025 · 5 min read
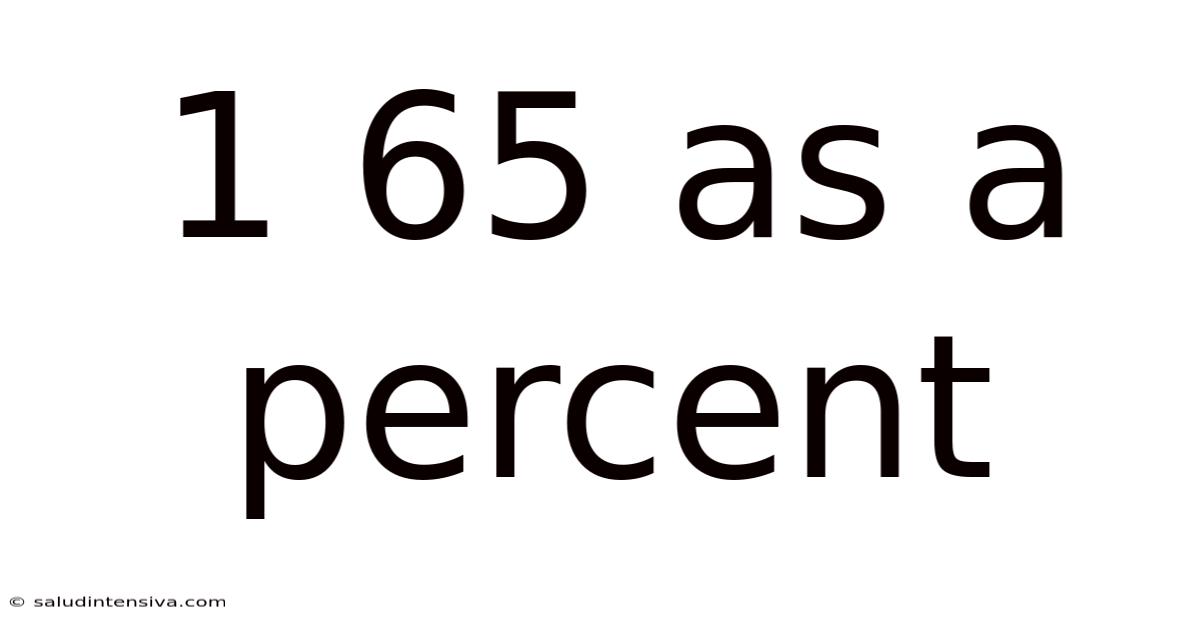
Table of Contents
Understanding 1/65 as a Percentage: A Comprehensive Guide
What does 1/65 represent as a percentage? This seemingly simple question opens the door to a deeper understanding of fractions, decimals, and percentages – fundamental concepts in mathematics with widespread applications in everyday life, from calculating discounts to understanding financial reports. This article will guide you through the process of converting 1/65 to a percentage, explaining the underlying principles and offering practical examples to solidify your understanding. We'll also explore related concepts and answer frequently asked questions.
Introduction: Fractions, Decimals, and Percentages – A Triad
Before diving into the specifics of 1/65, let's establish the relationship between fractions, decimals, and percentages. They are all different ways of expressing parts of a whole.
-
Fractions: Represent a part of a whole using a numerator (top number) and a denominator (bottom number). For example, 1/65 means one part out of 65 equal parts.
-
Decimals: Represent a part of a whole using base-ten notation. They are essentially fractions where the denominator is a power of 10 (10, 100, 1000, etc.).
-
Percentages: Represent a part of a whole as a fraction of 100. The percentage symbol (%) signifies "per hundred."
These three forms are interchangeable. We can convert a fraction to a decimal, a decimal to a percentage, and so on. This interconversion is crucial for various mathematical calculations and real-world applications.
Converting 1/65 to a Decimal
The first step in converting 1/65 to a percentage is converting it to a decimal. We achieve this by dividing the numerator (1) by the denominator (65):
1 ÷ 65 ≈ 0.0153846
The result is an approximate decimal because the division produces a non-terminating decimal (a decimal that goes on forever without repeating). We'll round this to a manageable number of decimal places for further calculations. For this example, we’ll use four decimal places: 0.0154. The more decimal places you use, the more accurate your final percentage will be.
Converting the Decimal to a Percentage
Now that we have the decimal equivalent (approximately 0.0154), converting it to a percentage is straightforward. We simply multiply the decimal by 100 and add the percentage symbol (%):
0.0154 × 100 = 1.54%
Therefore, 1/65 is approximately 1.54%.
Understanding the Approximation
It's important to reiterate that our result is an approximation. The true decimal representation of 1/65 is a non-terminating, non-repeating decimal. The level of accuracy depends on the number of decimal places we choose to retain during the conversion process. Using more decimal places in the intermediate steps will yield a more precise percentage. For most practical purposes, however, 1.54% is sufficiently accurate.
Practical Applications of Percentage Calculations
The ability to convert fractions to percentages has numerous practical applications:
-
Financial Calculations: Calculating interest rates, discounts, tax rates, profit margins, and more. Understanding percentages is essential for budgeting, investing, and managing personal finances.
-
Statistical Analysis: Percentages are widely used to represent proportions and probabilities in various statistical analyses. They help in interpreting data and drawing meaningful conclusions.
-
Scientific Research: In fields like biology, chemistry, and physics, percentages are frequently used to express concentrations, yields, and error margins.
-
Everyday Life: Calculating tips in restaurants, understanding sale discounts, interpreting survey results, and comparing prices are just a few examples of how we use percentages daily.
Expanding on the Concept: Working with Larger Fractions
While 1/65 is a relatively small fraction, the principles discussed above apply equally to larger fractions. Let's consider a slightly more complex example: converting 27/65 to a percentage.
-
Convert to Decimal: 27 ÷ 65 ≈ 0.41538
-
Convert to Percentage: 0.41538 × 100 ≈ 41.54%
Therefore, 27/65 is approximately 41.54%.
This demonstrates that the method remains the same regardless of the numerator's value. The key steps are dividing the numerator by the denominator and then multiplying the resulting decimal by 100.
Advanced Techniques: Using a Calculator or Spreadsheet Software
While manual calculation is valuable for understanding the underlying principles, using a calculator or spreadsheet software significantly simplifies the process, particularly for more complex fractions. Most calculators have a percentage function that directly calculates the percentage equivalent of a fraction. Spreadsheet software like Microsoft Excel or Google Sheets provides even more advanced functionalities, enabling quick and accurate conversion of multiple fractions simultaneously.
Frequently Asked Questions (FAQ)
Q: What if the fraction involves a number larger than the denominator?
A: If the numerator is larger than the denominator, the fraction is an improper fraction, representing a value greater than 1. Convert it to a mixed number (a whole number and a proper fraction) before converting to a decimal and then a percentage. For example, 66/65 = 1 1/65. Convert 1/65 to a decimal and add 1 to it before multiplying by 100.
Q: How many decimal places should I use?
A: The number of decimal places you use depends on the required level of accuracy. For most everyday applications, two or three decimal places are sufficient. For more precise calculations, especially in scientific or financial contexts, you might need more decimal places.
Q: Are there any shortcuts for converting fractions to percentages?
A: While there isn't a universal shortcut, understanding that percentage means "per hundred" can be helpful. If the denominator is a factor of 100 (e.g., 2, 4, 5, 10, 20, 25, 50), the conversion can sometimes be simplified mentally. For example, 1/4 is 25% because 4 goes into 100 twenty-five times (1/4 * 25/25 = 25/100 = 25%). However, for fractions with denominators that aren't factors of 100, using division and multiplication is the most reliable method.
Q: Can I use online calculators for this conversion?
A: Yes, numerous online calculators are readily available to convert fractions to percentages instantly. These calculators are useful for quick conversions, but understanding the underlying process remains essential for solving more complex mathematical problems.
Conclusion: Mastering Percentage Conversions
Converting 1/65 to a percentage (approximately 1.54%) illustrates the fundamental relationship between fractions, decimals, and percentages. This seemingly simple conversion highlights the importance of understanding these core mathematical concepts and their wide-ranging applications in various aspects of life. By mastering these conversions, you equip yourself with a valuable tool for problem-solving in numerous fields, from everyday calculations to complex analytical tasks. Remember to always consider the level of accuracy required when rounding decimals and choosing the appropriate number of decimal places. Consistent practice and a clear understanding of the underlying principles will solidify your ability to perform these conversions with confidence.
Latest Posts
Latest Posts
-
134 Degrees F To K
Sep 12, 2025
-
3 25 Percent As A Decimal
Sep 12, 2025
-
Meter Per Second To Rpm
Sep 12, 2025
-
What Is Equal To 6 12
Sep 12, 2025
-
What Is 1 3 4 5
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about 1 65 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.