Is 7/16 Bigger Than 5/8
saludintensiva
Sep 12, 2025 · 6 min read
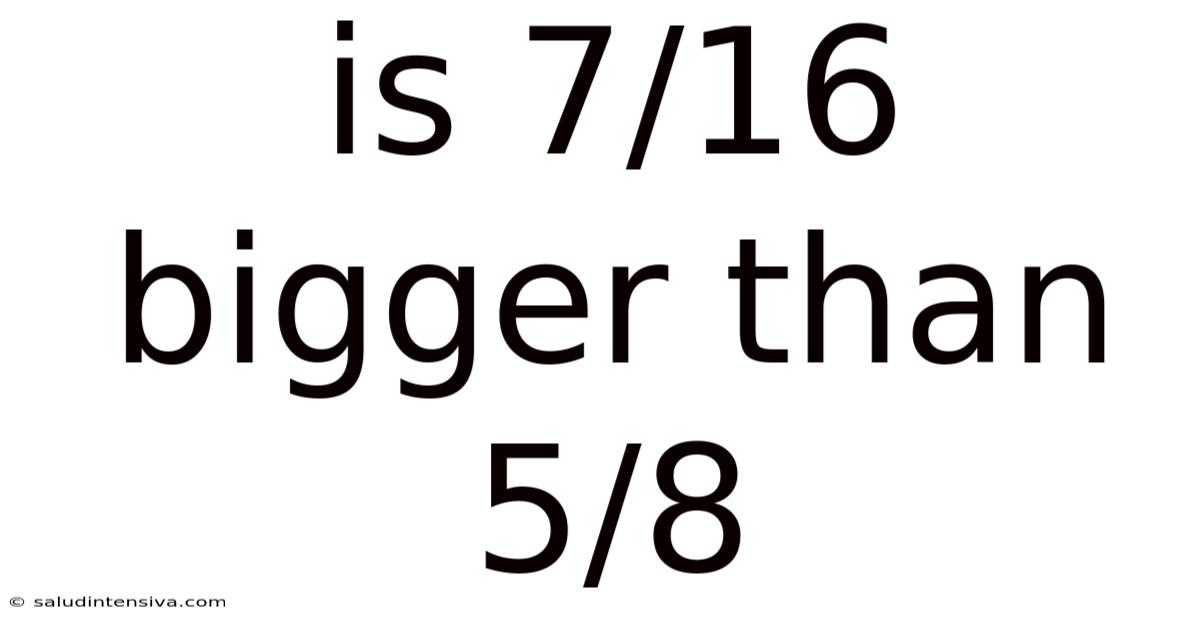
Table of Contents
Is 7/16 Bigger Than 5/8? A Deep Dive into Fraction Comparison
Many of us encounter fraction comparison in our daily lives, whether we're splitting a pizza, measuring ingredients for a recipe, or tackling math problems. Understanding how to compare fractions is a fundamental skill with practical applications far beyond the classroom. This article will thoroughly explore the question, "Is 7/16 bigger than 5/8?", and delve into various methods for comparing fractions, ensuring you gain a comprehensive understanding of the topic. We'll cover different approaches, including finding common denominators, converting to decimals, and using visual aids. By the end, you'll not only know the answer to our central question but also possess the tools to confidently compare any two fractions.
Understanding Fractions: A Quick Recap
Before we dive into comparing 7/16 and 5/8, let's refresh our understanding of fractions. A fraction represents a part of a whole. It consists of two numbers: the numerator (the top number) and the denominator (the bottom number). The numerator indicates how many parts we have, while the denominator indicates how many equal parts the whole is divided into. For example, in the fraction 3/4, the numerator is 3 and the denominator is 4, meaning we have 3 out of 4 equal parts.
Method 1: Finding a Common Denominator
The most common and reliable method for comparing fractions is to find a common denominator. This means finding a number that is a multiple of both denominators. Once we have a common denominator, we can directly compare the numerators.
Let's apply this to our problem: Is 7/16 bigger than 5/8?
-
Step 1: Find the least common multiple (LCM) of the denominators. The denominators are 16 and 8. The multiples of 8 are 8, 16, 24, 32... and the multiples of 16 are 16, 32, 48... The least common multiple is 16.
-
Step 2: Convert the fractions to equivalent fractions with the common denominator.
- 7/16 already has a denominator of 16, so it remains 7/16.
- To convert 5/8 to an equivalent fraction with a denominator of 16, we multiply both the numerator and the denominator by 2: (5 x 2) / (8 x 2) = 10/16.
-
Step 3: Compare the numerators. Now we compare 7/16 and 10/16. Since 7 < 10, we conclude that 7/16 < 10/16.
-
Step 4: State the conclusion. Therefore, 7/16 is not bigger than 5/8. In fact, 7/16 is smaller than 5/8.
Method 2: Converting to Decimals
Another effective method for comparing fractions is to convert them to decimals. This involves dividing the numerator by the denominator.
-
Step 1: Convert 7/16 to a decimal. 7 ÷ 16 = 0.4375
-
Step 2: Convert 5/8 to a decimal. 5 ÷ 8 = 0.625
-
Step 3: Compare the decimals. Since 0.4375 < 0.625, we conclude that 7/16 < 5/8.
This method confirms our previous finding: 7/16 is smaller than 5/8.
Method 3: Visual Representation
Visual aids can be particularly helpful for understanding fraction comparison, especially for beginners. Imagine two identical circles.
-
Representing 7/16: Divide one circle into 16 equal slices and shade 7 of them.
-
Representing 5/8: Divide the other circle into 8 equal slices and shade 5 of them.
By visually comparing the shaded areas, you'll readily see that the shaded area representing 5/8 is larger than the shaded area representing 7/16. This visual approach reinforces the concept and makes the comparison more intuitive.
Understanding the Relationship Between 7/16 and 5/8
The comparison reveals a significant difference between 7/16 and 5/8. 5/8 is considerably larger. Understanding this relationship is crucial for various applications. For example, if you're measuring ingredients for a recipe, using 7/16 instead of 5/8 could significantly alter the final outcome.
The difference between the two fractions is 10/16 - 7/16 = 3/16. This represents the numerical difference between the two values, highlighting how much larger 5/8 is compared to 7/16.
Extending the Knowledge: Comparing Fractions with Different Numerators and Denominators
The methods discussed above can be applied to any pair of fractions, regardless of their numerators and denominators. The key is to choose the method that you find most comfortable and efficient. For complex fractions, finding a common denominator often provides the most straightforward approach. For simpler fractions, converting to decimals might be quicker.
Remember, the ultimate goal is to express the fractions in a way that allows for a direct comparison of their relative sizes.
Frequently Asked Questions (FAQs)
Q1: What is the easiest way to compare fractions?
A1: The easiest method often depends on the specific fractions. For fractions with easily found common denominators, that is usually the most straightforward approach. Converting to decimals can also be quick and easy, especially for smaller fractions.
Q2: Can I use a calculator to compare fractions?
A2: Yes, calculators can be used to convert fractions to decimals, which then allows for easy comparison. Many calculators also have built-in fraction functionality that can directly compare fractions.
Q3: Why is finding a common denominator important?
A3: Finding a common denominator allows us to directly compare the numerators. This avoids the confusion and potential for errors that can arise from comparing fractions with different denominators directly. It's the foundation of accurate fraction comparison.
Q4: Are there any shortcuts for comparing fractions?
A4: While there aren't strict "shortcuts," understanding fraction benchmarks (like 1/2, 1/4, etc.) can help in making quick estimations. For instance, if one fraction is clearly less than 1/2 and another is clearly greater than 1/2, the comparison is straightforward.
Q5: What if the fractions are mixed numbers (a whole number and a fraction)?
A5: To compare mixed numbers, you can either convert them to improper fractions (where the numerator is greater than the denominator) and then use the methods described above, or compare the whole number parts first, and then compare the fractional parts if the whole number parts are equal.
Conclusion
Determining whether 7/16 is bigger than 5/8 involves understanding fundamental fraction concepts and applying appropriate comparison methods. Through finding a common denominator, converting to decimals, or employing visual aids, we've conclusively shown that 7/16 is smaller than 5/8. This article not only answered the initial question but also equipped you with the knowledge and tools to confidently compare any two fractions, enhancing your mathematical skills and problem-solving abilities. Remember to practice using different methods to build your understanding and find the approach that best suits your individual learning style. Mastering fraction comparison is a valuable skill with applications across various fields, from baking to engineering.
Latest Posts
Latest Posts
-
Convert Grams To Dwt Calculator
Sep 12, 2025
-
Convert 55 C To Fahrenheit
Sep 12, 2025
-
1 To The 5th Power
Sep 12, 2025
-
30 Days From May 6
Sep 12, 2025
-
8 Squared 15 Squared
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about Is 7/16 Bigger Than 5/8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.