Is 7/32 Bigger Than 3/16
saludintensiva
Sep 19, 2025 · 5 min read
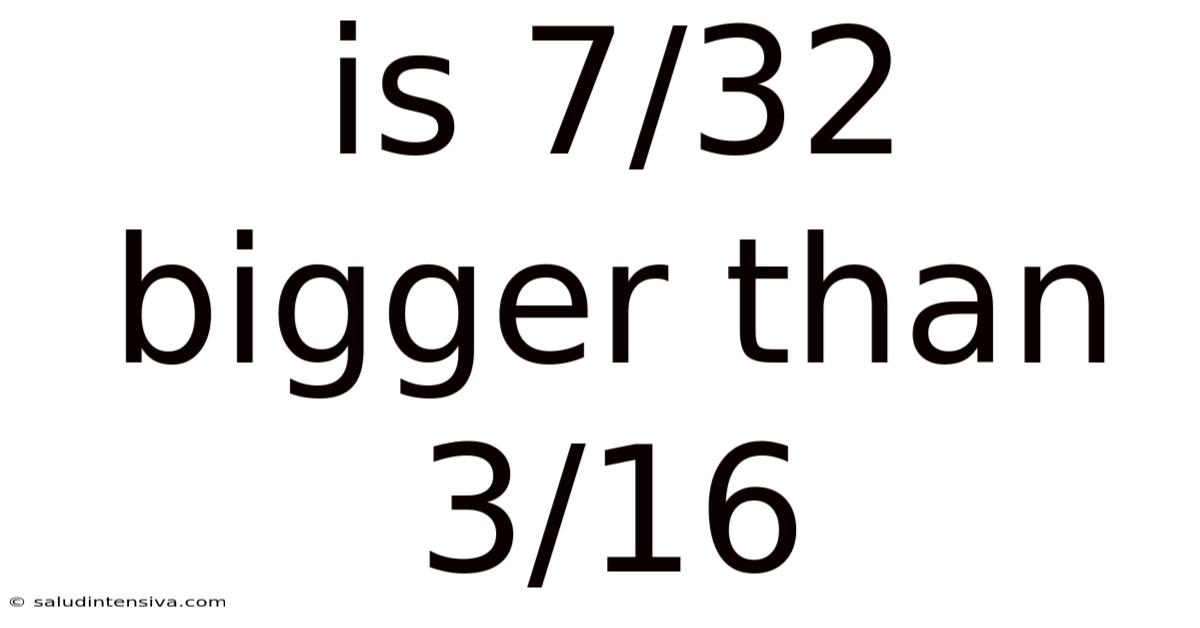
Table of Contents
Is 7/32 Bigger Than 3/16? A Deep Dive into Fraction Comparison
Comparing fractions might seem like a simple task, especially for smaller numbers. However, understanding the underlying principles allows you to confidently tackle even more complex fraction comparisons, building a strong foundation in mathematics. This article will explore the question, "Is 7/32 bigger than 3/16?", providing a step-by-step explanation, exploring different methods, and delving into the mathematical concepts involved. This will not only answer the immediate question but also equip you with the tools to compare any two fractions effectively.
Introduction: Understanding Fractions
Before we dive into the comparison, let's quickly review what fractions represent. A fraction, such as 7/32 or 3/16, represents a part of a whole. The top number is called the numerator, indicating how many parts we have. The bottom number is the denominator, showing the total number of equal parts the whole is divided into. Therefore, 7/32 means we have 7 out of 32 equal parts, while 3/16 means we have 3 out of 16 equal parts. Understanding this fundamental concept is crucial for comparing fractions.
Method 1: Finding a Common Denominator
The most straightforward method for comparing fractions is to find a common denominator. This means finding a number that is a multiple of both denominators (32 and 16). In this case, 32 is a multiple of 16 (16 x 2 = 32), so 32 is our common denominator.
-
Convert 3/16 to a fraction with a denominator of 32: To change the denominator from 16 to 32, we multiply both the numerator and the denominator by 2: (3 x 2) / (16 x 2) = 6/32.
-
Compare the fractions: Now we can easily compare 7/32 and 6/32. Since 7 > 6, we can conclude that 7/32 is bigger than 6/32.
-
Therefore: 7/32 is bigger than 3/16.
Method 2: Converting to Decimals
Another effective method is to convert both fractions to decimals. This allows for a direct numerical comparison.
-
Convert 7/32 to a decimal: Divide the numerator (7) by the denominator (32): 7 ÷ 32 ≈ 0.21875
-
Convert 3/16 to a decimal: Divide the numerator (3) by the denominator (16): 3 ÷ 16 = 0.1875
-
Compare the decimals: Since 0.21875 > 0.1875, we can conclude that 7/32 is bigger than 3/16.
Method 3: Using Cross-Multiplication
Cross-multiplication provides a quick and efficient way to compare fractions without finding a common denominator or converting to decimals.
-
Cross-multiply: Multiply the numerator of the first fraction (7) by the denominator of the second fraction (16): 7 x 16 = 112
-
Cross-multiply: Multiply the numerator of the second fraction (3) by the denominator of the first fraction (32): 3 x 32 = 96
-
Compare the products: Since 112 > 96, the fraction with the larger product (7/32) is the bigger fraction.
-
Therefore: 7/32 is bigger than 3/16.
Visual Representation: Understanding the Magnitude
While mathematical methods are precise, visualizing fractions can enhance understanding. Imagine two identical pizzas. One pizza is cut into 32 equal slices, and you take 7 slices (7/32). The other pizza is cut into 16 equal slices, and you take 3 slices (3/16). Visually, it becomes apparent that 7 out of 32 slices represents a larger portion than 3 out of 16 slices. Although the difference might seem subtle, the mathematical methods confirm this visual intuition.
Simplifying Fractions: A Preliminary Step
Before applying any comparison method, it's always a good idea to simplify the fractions if possible. Simplifying means reducing the fraction to its lowest terms by dividing both the numerator and the denominator by their greatest common divisor (GCD). In this case, 3/16 is already in its simplest form, as 3 and 16 have no common divisors other than 1. Similarly, 7/32 is also in its simplest form. This step, while not essential for this particular problem, is a valuable habit to develop when working with fractions.
The Importance of Understanding the Process
The question "Is 7/32 bigger than 3/16?" is more than just a simple arithmetic problem. It's a gateway to understanding fundamental concepts in fractions and developing crucial mathematical skills. Mastering these techniques allows you to confidently tackle more complex fraction problems, which are fundamental to various areas of mathematics and real-world applications.
Further Exploration: Extending the Concepts
The methods discussed here can be applied to compare any two fractions, regardless of their complexity. The key is to understand the underlying principles of finding common denominators, converting to decimals, or using cross-multiplication. These techniques are building blocks for more advanced mathematical concepts, such as working with mixed numbers, improper fractions, and solving equations involving fractions.
Frequently Asked Questions (FAQ)
-
Q: Can I use a calculator to compare fractions? A: Yes, you can use a calculator to convert fractions to decimals, providing a direct comparison. However, understanding the manual methods remains crucial for building mathematical understanding and problem-solving skills.
-
Q: Are there other methods to compare fractions? A: Yes, there are other less common methods, but the ones discussed here are the most efficient and widely used.
-
Q: What if the fractions have very large numbers? A: The methods remain the same, but the calculations might become more complex. Using a calculator can be helpful in such cases, but the underlying principles stay consistent.
-
Q: Why is finding a common denominator important? A: Finding a common denominator allows us to directly compare the numerators, simplifying the comparison process. It's like comparing apples to apples, ensuring a fair and accurate comparison.
-
Q: Why is simplifying fractions helpful? A: Simplifying fractions makes them easier to work with and reduces the risk of errors in calculations. It presents the fraction in its most efficient form.
Conclusion: Building a Strong Mathematical Foundation
Comparing fractions, like 7/32 and 3/16, might initially seem trivial, but it's a vital step in building a strong foundation in mathematics. By mastering the different methods presented here, you not only solve this particular problem but also develop crucial problem-solving skills applicable to a wide range of mathematical concepts and real-world scenarios. Remember, the goal is not just to find the answer but to understand the why behind the process. This understanding will serve you well in your future mathematical endeavors. So, to reiterate, yes, 7/32 is bigger than 3/16. But more importantly, you now understand how and why.
Latest Posts
Latest Posts
-
4 Square Root Of 256
Sep 19, 2025
-
What Is 2 6m In Feet
Sep 19, 2025
-
1 2 Raised To 2
Sep 19, 2025
-
475 Degrees F To Celsius
Sep 19, 2025
-
What Was 18 Weeks Ago
Sep 19, 2025
Related Post
Thank you for visiting our website which covers about Is 7/32 Bigger Than 3/16 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.