L.c.m Of 8 And 10
saludintensiva
Sep 12, 2025 · 6 min read
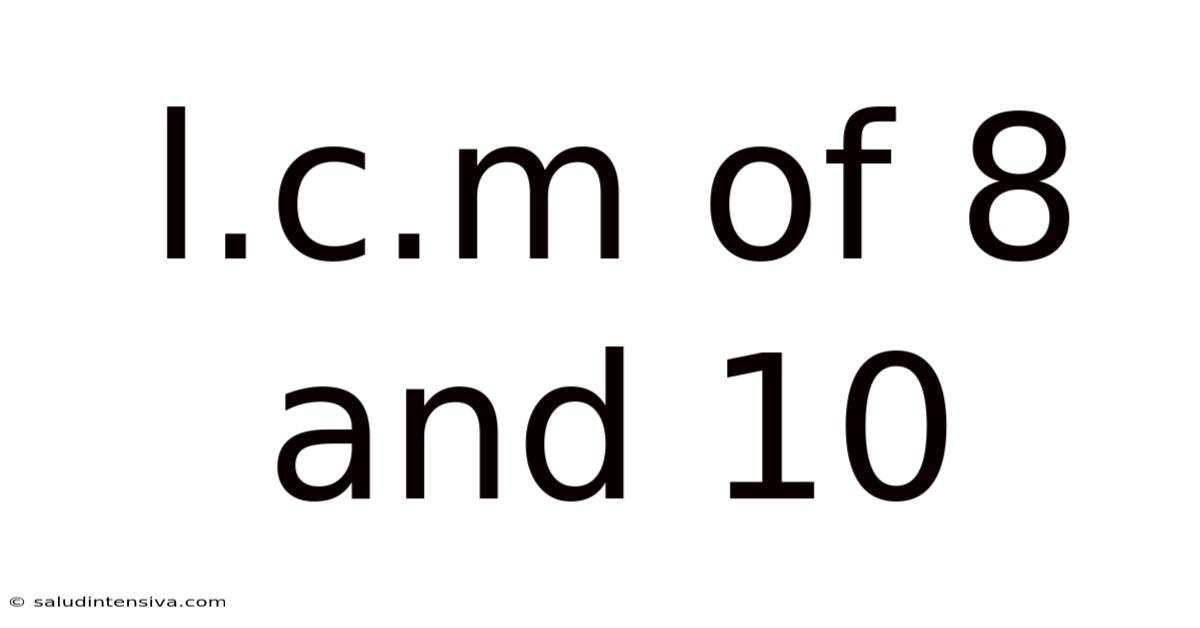
Table of Contents
Unveiling the Secrets of LCM: A Deep Dive into the Least Common Multiple of 8 and 10
Finding the least common multiple (LCM) might seem like a simple arithmetic task, but understanding the underlying concepts unlocks a world of mathematical possibilities. This comprehensive guide will explore the LCM of 8 and 10, delving into various methods for calculation, practical applications, and the broader significance of LCM in mathematics. We'll move beyond a simple answer and equip you with a thorough understanding of this fundamental concept.
Understanding Least Common Multiple (LCM)
Before we tackle the LCM of 8 and 10 specifically, let's establish a solid foundation. The least common multiple of two or more integers is the smallest positive integer that is a multiple of all the integers. In simpler terms, it's the smallest number that all the given numbers can divide into evenly. Understanding this definition is crucial for grasping the practical applications of LCM in various fields.
Think of it like coordinating schedules: if you need to perform two tasks that take 8 and 10 units of time respectively, the LCM will tell you the shortest time interval when both tasks can be completed simultaneously. This is just one example of the numerous real-world applications of LCM.
Method 1: Listing Multiples
This is the most straightforward method, especially for smaller numbers like 8 and 10. We simply list the multiples of each number until we find the smallest common multiple.
- Multiples of 8: 8, 16, 24, 32, 40, 48, 56, 64, 72, 80, ...
- Multiples of 10: 10, 20, 30, 40, 50, 60, 70, 80, 90, 100, ...
By comparing the lists, we can see that the smallest number appearing in both lists is 40. Therefore, the LCM of 8 and 10 is 40. This method is intuitive but can become cumbersome with larger numbers.
Method 2: Prime Factorization
This method is more efficient for larger numbers and provides a deeper understanding of the underlying mathematical principles. It involves breaking down each number into its prime factors. Prime factors are numbers that are only divisible by 1 and themselves (e.g., 2, 3, 5, 7, 11, etc.).
Let's find the prime factorization of 8 and 10:
- 8 = 2 x 2 x 2 = 2³
- 10 = 2 x 5
Now, we identify the highest power of each prime factor present in either factorization:
- The highest power of 2 is 2³ = 8
- The highest power of 5 is 5¹ = 5
To find the LCM, we multiply these highest powers together:
LCM(8, 10) = 2³ x 5 = 8 x 5 = 40
This method is more systematic and efficient, especially when dealing with larger numbers or finding the LCM of multiple numbers.
Method 3: Using the Greatest Common Divisor (GCD)
The LCM and GCD (greatest common divisor) are closely related. There's a formula that connects them:
LCM(a, b) x GCD(a, b) = a x b
where 'a' and 'b' are the two numbers.
First, let's find the GCD of 8 and 10 using the Euclidean algorithm:
- Divide the larger number (10) by the smaller number (8): 10 ÷ 8 = 1 with a remainder of 2.
- Replace the larger number with the smaller number (8) and the smaller number with the remainder (2): 8 ÷ 2 = 4 with a remainder of 0.
- The GCD is the last non-zero remainder, which is 2. Therefore, GCD(8, 10) = 2.
Now, we can use the formula:
LCM(8, 10) = (8 x 10) / GCD(8, 10) = (80) / 2 = 40
This method is particularly useful when dealing with larger numbers where prime factorization might be more time-consuming.
Visualizing LCM with Venn Diagrams
Venn diagrams offer a visual representation that helps solidify understanding. We can represent the prime factors of 8 and 10 in a Venn diagram:
8 (2³ ) 10 (2 x 5)
/ \ / \
2 2 2 5
/ \ / \ / \ / \
2 2 2 2 2 2 5 5
The intersection represents the common factors (in this case, just one 2). The LCM is found by multiplying all the factors within the circles, including the common factor only once: 2 x 2 x 2 x 5 = 40
Real-World Applications of LCM
The concept of LCM transcends the realm of theoretical mathematics. It has practical applications in various fields, including:
- Scheduling: Determining the time when two or more cyclical events coincide (like the example of completing two tasks).
- Fraction Operations: Finding a common denominator when adding or subtracting fractions.
- Gear Ratios: Calculating the optimal gear ratios in mechanical systems.
- Music Theory: Identifying harmonic intervals and creating musical compositions.
- Construction and Engineering: Coordinating the timing of construction processes or the alignment of structural elements.
Frequently Asked Questions (FAQ)
Q: What happens if the two numbers are relatively prime (meaning their GCD is 1)?
A: If the GCD is 1, the LCM is simply the product of the two numbers. For example, the LCM of 9 and 10 (which are relatively prime) is 90 (9 x 10).
Q: Can I use a calculator to find the LCM?
A: Yes, many scientific calculators have a built-in function to calculate the LCM of two or more numbers. However, understanding the underlying methods is crucial for problem-solving and deeper comprehension.
Q: What if I need to find the LCM of more than two numbers?
A: The same methods apply, but you need to consider all the prime factors of all the numbers involved. The prime factorization method becomes especially useful in these situations. For example, to find the LCM of 8, 10, and 12, you would first find the prime factorization of each number and then multiply the highest powers of all the prime factors present.
Q: Is there a difference between LCM and GCF (Greatest Common Factor)?
A: Yes, the LCM is the smallest number that is a multiple of all the given numbers, while the GCF (also known as GCD) is the largest number that is a divisor of all the given numbers. They are inversely related; a larger GCF implies a smaller LCM and vice-versa.
Conclusion
Finding the LCM of 8 and 10, while seemingly simple, provides a stepping stone to understanding a fundamental concept with far-reaching applications. Whether you use the method of listing multiples, prime factorization, or the GCD relationship, the result remains the same: the LCM of 8 and 10 is 40. Mastering these calculation methods and appreciating the practical implications of LCM will undoubtedly enhance your mathematical skills and problem-solving abilities across numerous disciplines. The beauty of mathematics lies in its ability to connect seemingly disparate concepts, and the LCM exemplifies this connection beautifully. By delving deeper into the fundamentals, you unlock a wealth of mathematical insight and equip yourself to tackle more complex problems with confidence.
Latest Posts
Latest Posts
-
Convert 55 C To Fahrenheit
Sep 12, 2025
-
1 To The 5th Power
Sep 12, 2025
-
30 Days From May 6
Sep 12, 2025
-
8 Squared 15 Squared
Sep 12, 2025
-
27 Minutes Of An Hour
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about L.c.m Of 8 And 10 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.