Lcm Of 10 15 25
saludintensiva
Sep 13, 2025 · 5 min read
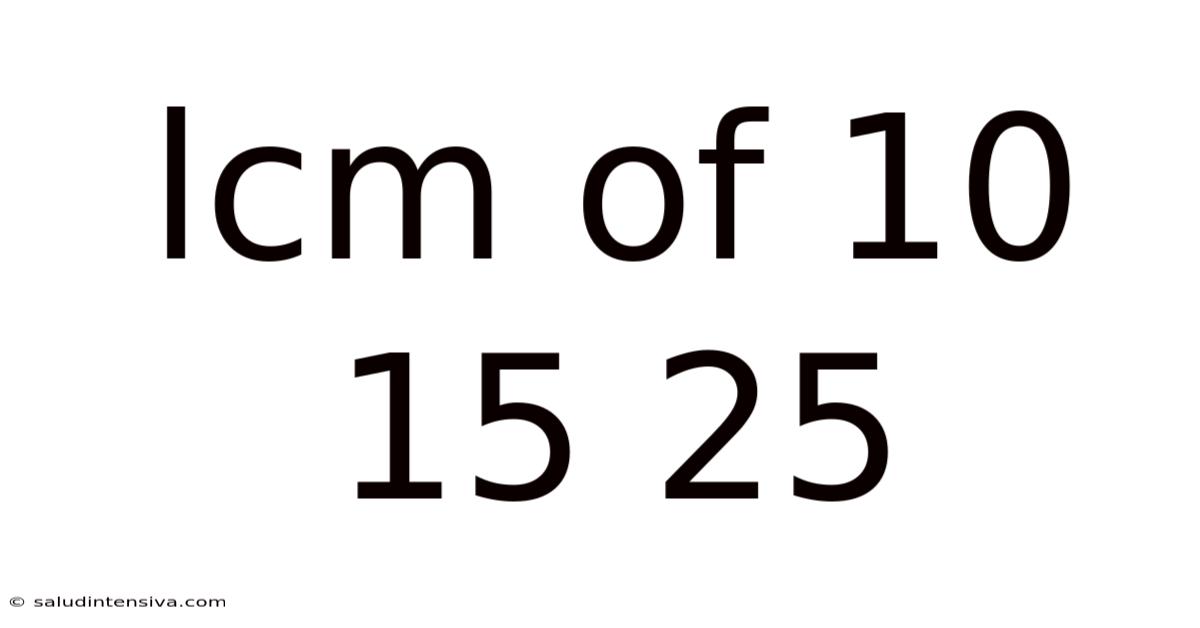
Table of Contents
Finding the Least Common Multiple (LCM) of 10, 15, and 25: A Comprehensive Guide
Finding the least common multiple (LCM) of a set of numbers is a fundamental concept in mathematics with applications ranging from simple fraction addition to complex scheduling problems. This article will delve into the process of calculating the LCM of 10, 15, and 25, exploring different methods and providing a deep understanding of the underlying principles. We'll cover everything from the basics of LCM to advanced techniques, ensuring a comprehensive understanding for learners of all levels. Understanding LCM is crucial for various mathematical operations and real-world applications.
Understanding Least Common Multiple (LCM)
Before we dive into calculating the LCM of 10, 15, and 25, let's establish a clear understanding of what LCM actually means. The least common multiple of two or more integers is the smallest positive integer that is divisible by all the integers in the set. In simpler terms, it's the smallest number that all the numbers in the set can divide into evenly without leaving a remainder.
For example, consider the numbers 2 and 3. The multiples of 2 are 2, 4, 6, 8, 10, and so on. The multiples of 3 are 3, 6, 9, 12, 15, and so on. The common multiples of 2 and 3 are 6, 12, 18, and so on. The least common multiple, therefore, is 6.
Method 1: Listing Multiples
This is the most straightforward method, particularly useful for smaller numbers. We list the multiples of each number until we find the smallest common multiple.
- Multiples of 10: 10, 20, 30, 40, 50, 60, 70, 80, 90, 100, 150...
- Multiples of 15: 15, 30, 45, 60, 75, 90, 105, 120, 135, 150...
- Multiples of 25: 25, 50, 75, 100, 125, 150...
By inspecting the lists, we can see that the smallest number appearing in all three lists is 150. Therefore, the LCM of 10, 15, and 25 is 150. While simple for smaller numbers, this method becomes cumbersome and inefficient for larger numbers.
Method 2: Prime Factorization
This method is more efficient and works well for larger numbers. It involves finding the prime factorization of each number and then constructing the LCM from the prime factors.
-
Find the prime factorization of each number:
- 10 = 2 x 5
- 15 = 3 x 5
- 25 = 5 x 5 = 5²
-
Identify the highest power of each prime factor:
- The prime factors are 2, 3, and 5.
- The highest power of 2 is 2¹ = 2
- The highest power of 3 is 3¹ = 3
- The highest power of 5 is 5² = 25
-
Multiply the highest powers together:
LCM(10, 15, 25) = 2 x 3 x 25 = 150
Therefore, the LCM of 10, 15, and 25 is 150 using the prime factorization method. This method is generally preferred for its efficiency, especially when dealing with larger numbers.
Method 3: Greatest Common Divisor (GCD) and LCM Relationship
The LCM and the greatest common divisor (GCD) of a set of numbers are closely related. The product of the LCM and GCD of two numbers is equal to the product of the two numbers. While this relationship is most easily applied to two numbers, it can be extended to multiple numbers using iterative calculations.
-
Find the GCD of 10 and 15 using the Euclidean algorithm:
- 15 = 1 x 10 + 5
- 10 = 2 x 5 + 0
- The GCD(10, 15) = 5
-
Find the LCM of 10 and 15:
- LCM(10, 15) = (10 x 15) / GCD(10, 15) = (10 x 15) / 5 = 30
-
Find the GCD of 30 and 25:
- 30 = 1 x 25 + 5
- 25 = 5 x 5 + 0
- The GCD(30, 25) = 5
-
Find the LCM of 30 and 25:
- LCM(30, 25) = (30 x 25) / GCD(30, 25) = (30 x 25) / 5 = 150
Therefore, the LCM of 10, 15, and 25 is 150 using the GCD method. This method showcases the interconnectedness of LCM and GCD, providing a deeper understanding of their relationship.
Applications of LCM
The concept of LCM has wide-ranging applications in various fields:
- Fraction Addition and Subtraction: Finding the LCM of the denominators is crucial for adding or subtracting fractions with different denominators.
- Scheduling Problems: Determining when events will occur simultaneously (e.g., buses arriving at a stop at the same time).
- Cyclic Processes: Analyzing repeating patterns or cycles in various systems.
- Music Theory: Calculating the least common multiple of note durations to determine the rhythmic patterns in music.
- Computer Science: In various algorithms and data structure implementations.
Frequently Asked Questions (FAQ)
Q: What is the difference between LCM and GCD?
A: The least common multiple (LCM) is the smallest number that is a multiple of all the given numbers. The greatest common divisor (GCD) is the largest number that divides all the given numbers without leaving a remainder.
Q: Is there a formula for calculating the LCM of three or more numbers?
A: There isn't a single, direct formula like there is for two numbers. However, the prime factorization method and the iterative GCD method can efficiently handle any number of inputs.
Q: Can the LCM of a set of numbers be larger than the largest number in the set?
A: Yes, absolutely. The LCM is often larger than the largest number in the set, especially when the numbers don't share common factors.
Q: What if one of the numbers is zero?
A: The LCM of any set of numbers that includes zero is undefined. Zero has infinitely many multiples, making it impossible to determine the least common multiple.
Conclusion
Calculating the least common multiple is a fundamental skill in mathematics with practical applications in diverse fields. We've explored three methods for finding the LCM of 10, 15, and 25: listing multiples, prime factorization, and utilizing the relationship between LCM and GCD. The prime factorization method is generally the most efficient and applicable to a wider range of numbers. Understanding the LCM and its related concepts strengthens your mathematical foundation and opens doors to solving more complex problems. Mastering these techniques empowers you to tackle various mathematical challenges with confidence and efficiency. Remember, the key is to choose the method best suited to the numbers involved and to understand the underlying principles. With practice, calculating LCM will become second nature.
Latest Posts
Latest Posts
-
9 Divided By 1 2
Sep 13, 2025
-
7 Out Of 13 Percentage
Sep 13, 2025
-
14 Acres In Square Feet
Sep 13, 2025
-
90 Days After August 15
Sep 13, 2025
-
5 6 Is Equivalent To
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 10 15 25 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.