Lcm Of 2 7 3
saludintensiva
Sep 13, 2025 · 5 min read
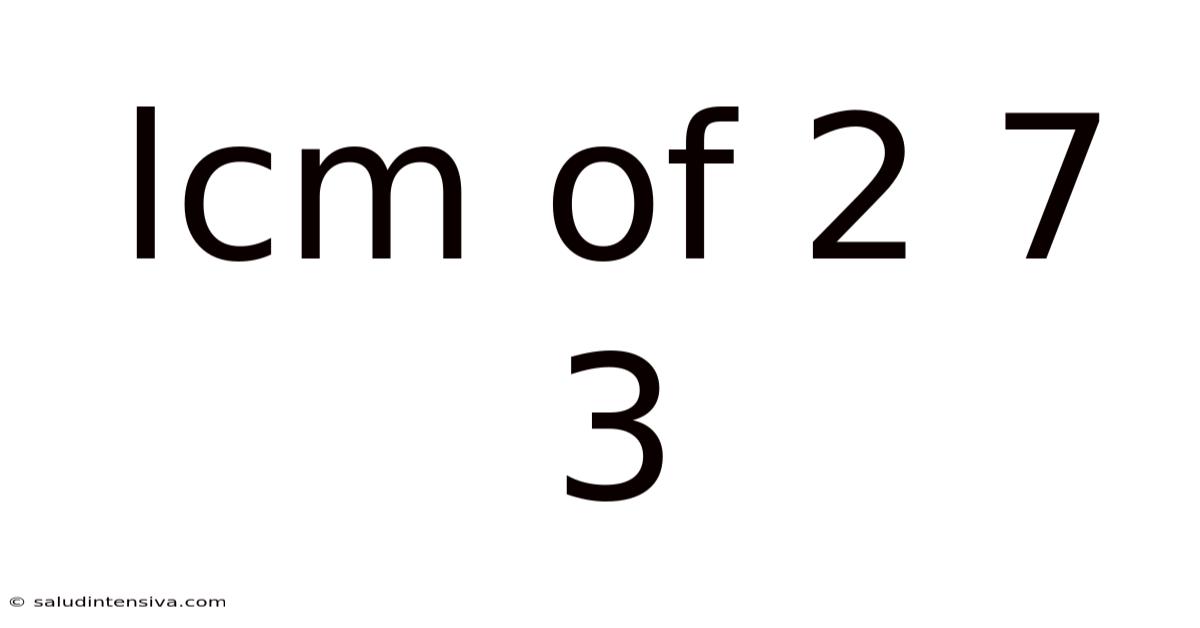
Table of Contents
Finding the Least Common Multiple (LCM) of 2, 7, and 3: A Comprehensive Guide
Finding the least common multiple (LCM) of a set of numbers is a fundamental concept in mathematics, crucial for various applications, from simplifying fractions to solving problems in algebra and beyond. This article provides a comprehensive guide to calculating the LCM of 2, 7, and 3, explaining the process step-by-step and exploring different methods. We'll delve into the underlying principles, offering insights that extend beyond this specific example to help you master LCM calculations for any set of numbers.
Understanding Least Common Multiple (LCM)
The least common multiple (LCM) of two or more integers is the smallest positive integer that is a multiple of all the integers. In simpler terms, it's the smallest number that all the given numbers can divide into evenly. For example, the LCM of 2 and 3 is 6 because 6 is the smallest number divisible by both 2 and 3. Understanding LCM is essential in various mathematical operations, including simplifying fractions, solving equations, and working with rhythmic patterns in music.
Method 1: Listing Multiples
This method is straightforward, especially for smaller numbers. We list the multiples of each number until we find the smallest multiple common to all three.
- Multiples of 2: 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 21, 22, 24, 26, 28, 30, 32, 34, 36, 38, 40, 42...
- Multiples of 7: 7, 14, 21, 28, 35, 42, 49...
- Multiples of 3: 3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33, 36, 39, 42...
By examining the lists, we observe that the smallest number appearing in all three lists is 42. Therefore, the LCM of 2, 7, and 3 is 42.
While this method works well for small numbers, it becomes less efficient with larger numbers. Let's explore more sophisticated and efficient methods.
Method 2: Prime Factorization
Prime factorization is a powerful technique for finding the LCM of any set of numbers, regardless of size. It involves expressing each number as a product of its prime factors. A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself (e.g., 2, 3, 5, 7, 11...).
-
Find the prime factorization of each number:
- 2 = 2¹
- 7 = 7¹
- 3 = 3¹
-
Identify the highest power of each prime factor: In this case, we have three distinct prime factors: 2, 3, and 7. The highest power of each is 2¹, 3¹, and 7¹.
-
Multiply the highest powers together: LCM(2, 7, 3) = 2¹ × 3¹ × 7¹ = 2 × 3 × 7 = 42
Therefore, the LCM of 2, 7, and 3 is 42. This method is far more efficient than listing multiples, especially when dealing with larger numbers or a greater number of integers.
Method 3: Greatest Common Divisor (GCD) Method
The LCM and GCD (greatest common divisor) of a set of numbers are related. We can use the GCD to find the LCM using the following formula:
LCM(a, b, c) = (|a × b × c|) / GCD(a, b, c)
However, this formula is best suited for two numbers. For three or more numbers, a more iterative approach using the GCD is needed. We can find the LCM of two numbers at a time and then find the LCM of the result and the remaining number. Let's demonstrate this:
-
Find the LCM of 2 and 7:
- Multiples of 2: 2, 4, 6, 8, 10, 12, 14...
- Multiples of 7: 7, 14, 21...
- LCM(2, 7) = 14
-
Find the LCM of 14 and 3:
- Multiples of 14: 14, 28, 42...
- Multiples of 3: 3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33, 36, 39, 42...
- LCM(14, 3) = 42
Therefore, the LCM of 2, 7, and 3 is 42. This method, while functional, is less efficient than prime factorization for larger sets of numbers.
Why is Understanding LCM Important?
The concept of LCM extends far beyond simple mathematical exercises. It finds practical applications in numerous areas, including:
-
Fraction Addition and Subtraction: To add or subtract fractions with different denominators, you need to find the LCM of the denominators to create a common denominator.
-
Scheduling Problems: Imagine you have three events that occur at intervals of 2, 7, and 3 days, respectively. The LCM will tell you when all three events will coincide.
-
Cyclic Patterns: LCM is crucial in understanding repeating patterns, such as in musical rhythms or the cycles of celestial bodies.
Frequently Asked Questions (FAQ)
-
What is the difference between LCM and GCD? The LCM is the smallest common multiple, while the GCD is the largest common divisor. They are inversely related.
-
Can I use a calculator to find the LCM? Yes, many scientific and graphing calculators have built-in functions to calculate the LCM of multiple numbers.
-
What if the numbers have common factors? The prime factorization method easily accounts for common factors, as it considers only the highest power of each prime factor.
-
Is there a formula for finding the LCM of more than two numbers? While a direct formula is less common for more than two numbers, the prime factorization method provides an efficient and generalizable solution.
Conclusion:
Finding the LCM of 2, 7, and 3, while seemingly a simple task, highlights the importance of understanding fundamental mathematical concepts. We explored three distinct methods: listing multiples, prime factorization, and the GCD method. While listing multiples is suitable for small numbers, prime factorization provides a significantly more efficient and versatile approach, especially for larger numbers and more complex sets. Understanding LCM is not just about solving mathematical problems; it's about developing a deeper understanding of numerical relationships and their applications in various fields. Mastering this concept will equip you with a valuable tool for tackling more advanced mathematical challenges. The LCM of 2, 7, and 3 is definitively 42, and the methods discussed here provide a solid foundation for calculating the LCM of any set of integers you encounter.
Latest Posts
Latest Posts
-
18 Deg C To F
Sep 13, 2025
-
2 3 5 9 Simplify
Sep 13, 2025
-
How Long Is 162 Minutes
Sep 13, 2025
-
When Was 21 Weeks Ago
Sep 13, 2025
-
3 1 5 As A Decimal
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 2 7 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.