Lcm Of 27 And 24
saludintensiva
Sep 15, 2025 · 5 min read
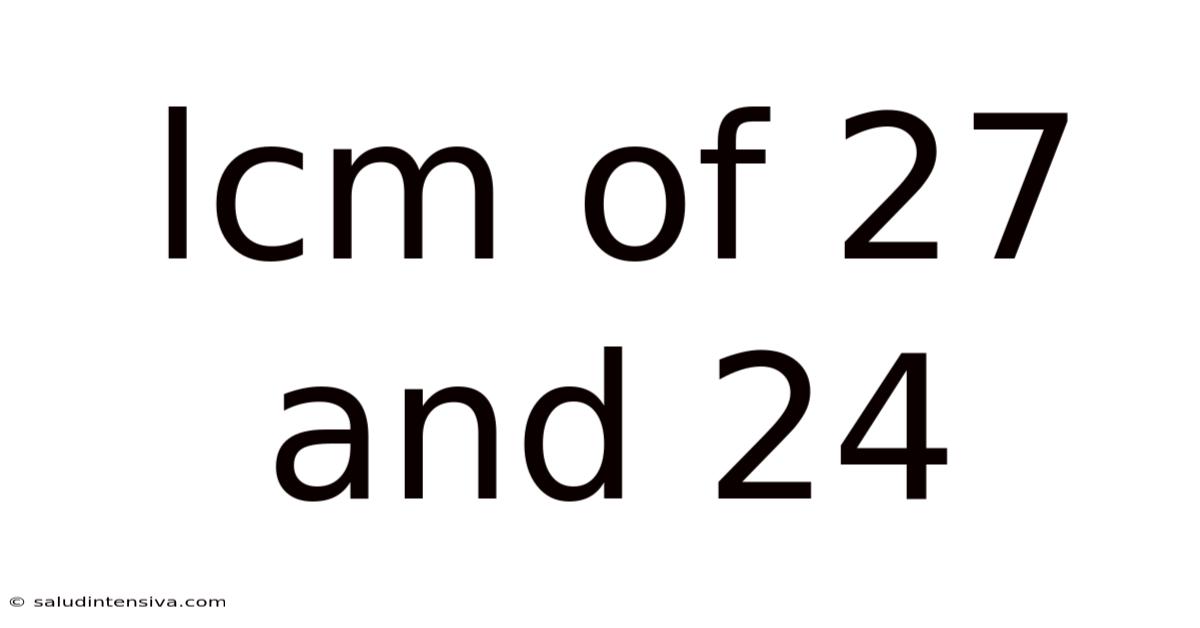
Table of Contents
Finding the Least Common Multiple (LCM) of 27 and 24: A Comprehensive Guide
Finding the least common multiple (LCM) might seem like a simple arithmetic task, but understanding the underlying principles and various methods for calculating it can greatly enhance your mathematical skills. This article delves deep into the concept of LCM, focusing specifically on finding the LCM of 27 and 24. We'll explore multiple methods, explain the reasoning behind each, and provide ample examples to solidify your understanding. This will not only help you solve this specific problem but also equip you to tackle similar problems with confidence.
Introduction to Least Common Multiple (LCM)
The least common multiple (LCM) of two or more integers is the smallest positive integer that is divisible by all the integers. It's a fundamental concept in number theory with applications in various fields, from simplifying fractions to solving problems in algebra and beyond. Understanding LCM is crucial for many mathematical operations. In this article, we will focus on finding the LCM of 27 and 24, demonstrating different approaches to reach the solution.
Method 1: Listing Multiples
The most straightforward method for finding the LCM of smaller numbers is by listing their multiples. Let's apply this to 27 and 24:
- Multiples of 27: 27, 54, 81, 108, 135, 162, 189, 216, 243, 270, ...
- Multiples of 24: 24, 48, 72, 96, 120, 144, 168, 192, 216, 240, 264, ...
By comparing the lists, we can identify the smallest common multiple. Notice that 216 appears in both lists. Therefore, the LCM of 27 and 24 is 216.
This method is effective for smaller numbers, but it becomes cumbersome and inefficient when dealing with larger numbers. Let's explore more efficient methods.
Method 2: Prime Factorization
Prime factorization is a powerful technique for finding the LCM of any set of integers. It involves breaking down each number into its prime factors – numbers divisible only by 1 and themselves.
-
Prime Factorization of 27: 27 = 3 x 9 = 3 x 3 x 3 = 3³
-
Prime Factorization of 24: 24 = 2 x 12 = 2 x 2 x 6 = 2 x 2 x 2 x 3 = 2³ x 3
Now, to find the LCM, we take the highest power of each prime factor present in the factorizations:
- The highest power of 2 is 2³ = 8
- The highest power of 3 is 3³ = 27
Therefore, the LCM(27, 24) = 2³ x 3³ = 8 x 27 = 216
This method is significantly more efficient than listing multiples, especially when working with larger numbers. It provides a systematic approach that avoids the trial-and-error aspect of the listing method.
Method 3: Using the Greatest Common Divisor (GCD)
The LCM and the greatest common divisor (GCD) are closely related. The product of the LCM and GCD of two numbers is equal to the product of the two numbers. In other words:
LCM(a, b) x GCD(a, b) = a x b
We can use this relationship to find the LCM if we already know the GCD.
-
Finding the GCD of 27 and 24: We can use the Euclidean algorithm to find the GCD.
- 27 = 1 x 24 + 3
- 24 = 8 x 3 + 0
The last non-zero remainder is 3, so GCD(27, 24) = 3
-
Calculating the LCM: LCM(27, 24) = (27 x 24) / GCD(27, 24) = (27 x 24) / 3 = 216
This method is particularly efficient when dealing with larger numbers where finding the prime factorization might be more time-consuming. The Euclidean algorithm provides a quick and efficient way to determine the GCD.
Understanding the Concept of Divisibility
The foundation of LCM lies in the concept of divisibility. A number 'a' is divisible by another number 'b' if the remainder is 0 when 'a' is divided by 'b'. The LCM represents the smallest number that satisfies the divisibility condition for all the given numbers. In our example, 216 is divisible by both 27 and 24, and it's the smallest number that possesses this property.
Applications of LCM
The LCM has a wide range of applications in various areas:
- Fractions: Finding the LCM of denominators is crucial when adding or subtracting fractions. It allows you to find a common denominator, simplifying the calculation.
- Scheduling: Determining when events with different periodicities will coincide (e.g., two buses arriving at a stop at different intervals).
- Gear Ratios: In mechanics, the LCM is used in calculations involving gear ratios to determine the speed and synchronization of rotating parts.
- Music Theory: Understanding the LCM is essential in music theory when dealing with rhythmic patterns and harmonic relationships.
Frequently Asked Questions (FAQ)
Q1: What if the numbers have no common factors other than 1?
If the numbers are relatively prime (their GCD is 1), then their LCM is simply their product. For example, the LCM of 15 and 28 is 15 x 28 = 420.
Q2: Can I use a calculator to find the LCM?
Many scientific calculators have built-in functions to calculate the LCM of two or more numbers. However, understanding the underlying methods is vital for a deeper understanding of the concept.
Q3: What if I have more than two numbers?
The same methods can be extended to find the LCM of more than two numbers. For prime factorization, you would consider the highest power of each prime factor present in the factorizations of all the numbers. For the GCD method, you would iteratively find the GCD of pairs of numbers and then use the relationship between LCM and GCD.
Q4: Why is the LCM important?
The LCM is a fundamental concept in number theory with wide-ranging applications. Understanding it is crucial for solving problems related to fractions, scheduling, and other areas. It allows you to find the smallest common multiple, which is essential for various calculations and real-world scenarios.
Conclusion
Finding the least common multiple is a crucial skill in mathematics. While the listing method provides a simple visual approach for small numbers, the prime factorization and GCD methods are significantly more efficient and versatile for larger numbers. Understanding these different approaches not only helps you solve the problem but also solidifies your grasp of core mathematical principles. Mastering the LCM equips you with a valuable tool for tackling various mathematical challenges and real-world applications. Remember to practice regularly to build confidence and fluency in this fundamental concept. The journey of understanding LCM might seem challenging at first, but with consistent effort and practice, you will be able to solve even the most complex problems with ease.
Latest Posts
Latest Posts
-
12 Weeks From May 1st
Sep 15, 2025
-
What Is 3 Times 1 5
Sep 15, 2025
-
5000 Square Feet To Acres
Sep 15, 2025
-
Linear Yard To Square Feet
Sep 15, 2025
-
Fractions Equal To 1 6
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 27 And 24 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.