Lcm Of 3 4 8
saludintensiva
Sep 16, 2025 · 6 min read
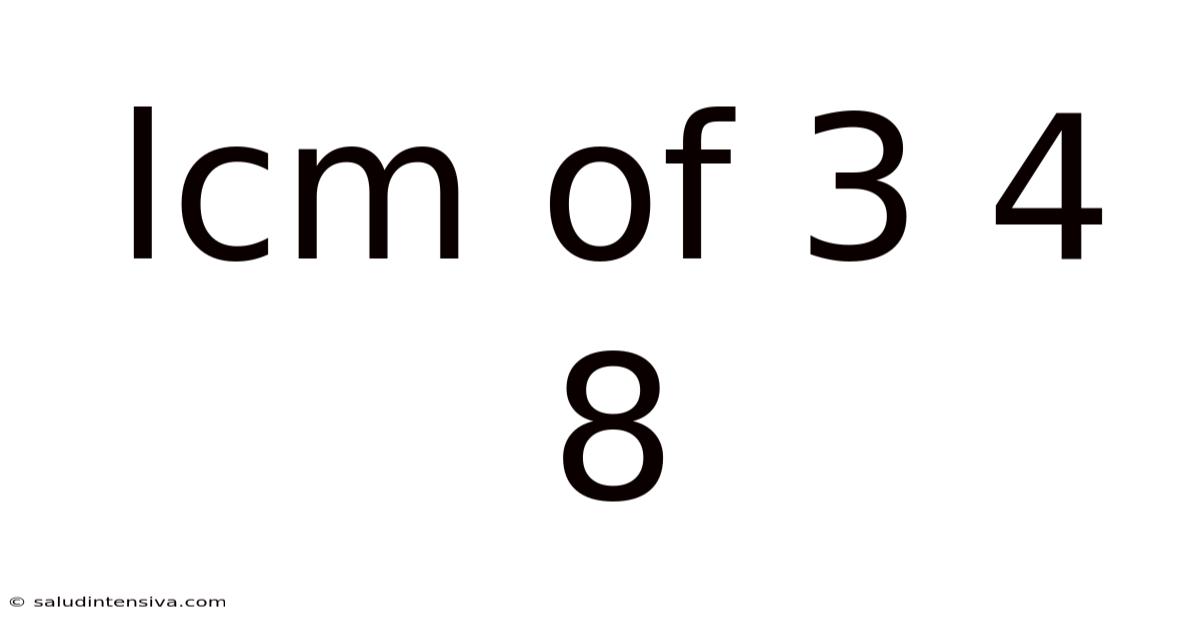
Table of Contents
Finding the Least Common Multiple (LCM) of 3, 4, and 8: A Comprehensive Guide
Finding the least common multiple (LCM) of a set of numbers is a fundamental concept in mathematics, crucial for various applications, from simplifying fractions to solving problems in algebra and beyond. This article will delve into the process of finding the LCM of 3, 4, and 8, explaining different methods and providing a thorough understanding of the underlying principles. We'll move beyond simply stating the answer and explore the 'why' behind the calculations, making this concept clear and accessible to everyone, regardless of their mathematical background.
Understanding Least Common Multiples (LCM)
Before we tackle the LCM of 3, 4, and 8 specifically, let's establish a clear understanding of what an LCM is. The least common multiple of two or more integers is the smallest positive integer that is a multiple of all the integers. In simpler terms, it's the smallest number that all the given numbers can divide into evenly without leaving a remainder.
For example, consider the numbers 2 and 3. The multiples of 2 are 2, 4, 6, 8, 10, 12… The multiples of 3 are 3, 6, 9, 12, 15… The smallest number that appears in both lists is 6. Therefore, the LCM of 2 and 3 is 6.
Method 1: Listing Multiples
The simplest method, especially for smaller numbers like 3, 4, and 8, is to list the multiples of each number until you find the smallest common multiple.
- Multiples of 3: 3, 6, 9, 12, 15, 18, 21, 24, 27, 30…
- Multiples of 4: 4, 8, 12, 16, 20, 24, 28, 32…
- Multiples of 8: 8, 16, 24, 32, 40…
By examining the lists, we can see that the smallest number that appears in all three lists is 24. Therefore, the LCM of 3, 4, and 8 is 24.
Method 2: Prime Factorization
This method is more efficient for larger numbers and provides a deeper understanding of the concept. It involves breaking down each number into its prime factors – numbers divisible only by 1 and themselves.
- Prime factorization of 3: 3 (3 is already a prime number)
- Prime factorization of 4: 2 x 2 = 2²
- Prime factorization of 8: 2 x 2 x 2 = 2³
Now, we identify the highest power of each prime factor present in the factorizations:
- The highest power of 2 is 2³ = 8
- The highest power of 3 is 3¹ = 3
To find the LCM, we multiply these highest powers together: 2³ x 3 = 8 x 3 = 24.
This method is particularly useful because it highlights the relationship between the numbers and their prime factors. It clearly shows why 24 is the LCM – it contains all the prime factors of 3, 4, and 8, raised to their highest powers.
Method 3: Greatest Common Divisor (GCD) and LCM Relationship
There's a powerful relationship between the LCM and the greatest common divisor (GCD) of two or more numbers. The GCD is the largest number that divides all the given numbers without leaving a remainder. The relationship is expressed by the following formula:
LCM(a, b) x GCD(a, b) = a x b
This formula works for two numbers (a and b). For more than two numbers, we can apply it iteratively. Let's use this method to find the LCM of 3, 4, and 8.
First, let's find the GCD of 3 and 4. Since 3 and 4 share no common factors other than 1, their GCD is 1.
Now, let's find the LCM of 3 and 4 using the formula:
LCM(3, 4) x GCD(3, 4) = 3 x 4 LCM(3, 4) x 1 = 12 LCM(3, 4) = 12
Next, we find the GCD of 12 and 8. The GCD of 12 and 8 is 4.
Now, we find the LCM of 12 and 8 using the formula:
LCM(12, 8) x GCD(12, 8) = 12 x 8 LCM(12, 8) x 4 = 96 LCM(12, 8) = 24
Therefore, the LCM of 3, 4, and 8 is 24. This method, while slightly more complex, showcases the interconnectedness of GCD and LCM concepts.
Visual Representation: Venn Diagram
While not a direct calculation method, a Venn diagram can be helpful in visualizing the prime factors and understanding the LCM. We represent each number's prime factorization in a Venn diagram.
For 3, we have {3} For 4, we have {2, 2} For 8, we have {2, 2, 2}
In a Venn diagram, the overlapping sections represent common factors. The LCM is found by multiplying all the factors within the diagram (including those that are not shared). This method provides a strong visual understanding of the prime factorization approach.
Applications of LCM
Understanding LCMs is crucial in various mathematical and real-world scenarios:
- Fraction addition and subtraction: Finding the LCM of the denominators is essential to find a common denominator before adding or subtracting fractions.
- Scheduling problems: Determining when events will occur simultaneously (e.g., buses arriving at a stop at the same time).
- Patterning and sequencing: Identifying when cycles in repeating patterns will align.
- Gear ratios and mechanical systems: Calculating the least common multiple of gear rotations.
- Music theory: Determining the least common multiple of note durations.
Frequently Asked Questions (FAQ)
Q: What if the numbers share common factors? The prime factorization method handles common factors efficiently. Only the highest power of each prime factor is included in the LCM calculation.
Q: Is there a shortcut for finding the LCM of three or more numbers? The prime factorization method is generally the most efficient shortcut for any number of integers.
Q: Can the LCM be larger than the largest number in the set? Yes, absolutely. The LCM is often larger than the largest number, particularly when the numbers do not share many common factors.
Q: What if one of the numbers is 0? The LCM of any set of numbers that includes 0 is undefined. Zero has an infinite number of multiples.
Q: Can I use a calculator to find the LCM? Many calculators, both physical and online, have built-in functions to calculate the LCM of multiple numbers.
Conclusion
Finding the least common multiple is a fundamental skill in mathematics with wide-ranging applications. While the simple method of listing multiples is suitable for smaller numbers, the prime factorization method offers a more efficient and insightful approach for larger numbers and provides a deeper understanding of the underlying mathematical principles. Mastering LCM calculations will enhance your problem-solving abilities in various mathematical contexts and real-world scenarios. We've explored multiple methods, highlighting their advantages and clarifying the underlying concepts to ensure a robust understanding of this essential mathematical tool. The LCM of 3, 4, and 8, as demonstrated through various methods, is definitively 24. Remember that consistent practice is key to solidifying your understanding and developing fluency in these important calculations.
Latest Posts
Latest Posts
-
71 200 As A Decimal
Sep 16, 2025
-
1 2 As A Mixed Number
Sep 16, 2025
-
Lcm Of 22 And 33
Sep 16, 2025
-
2 3 Acres To Square Feet
Sep 16, 2025
-
How Long Is 16 Hours
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 3 4 8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.