Lcm Of 5 And 5
saludintensiva
Sep 12, 2025 · 5 min read
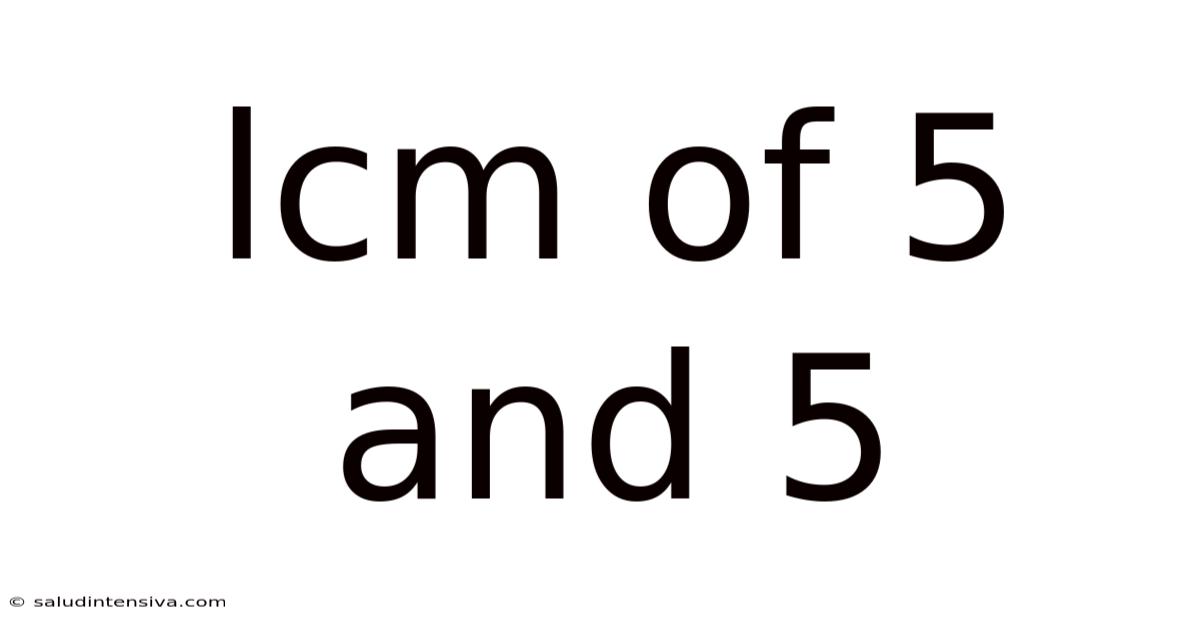
Table of Contents
Understanding the Least Common Multiple (LCM): A Deep Dive into LCM of 5 and 5
Finding the least common multiple (LCM) might seem like a simple task, especially when dealing with small numbers like 5 and 5. However, understanding the underlying principles behind LCM calculations is crucial for grasping more complex mathematical concepts. This article provides a comprehensive exploration of LCM, focusing specifically on the LCM of 5 and 5, and expanding to cover more general applications and advanced techniques. We'll delve into various methods for calculating LCM, explain the underlying mathematical theory, and address frequently asked questions. This in-depth guide ensures a thorough understanding of this fundamental mathematical concept.
Introduction to Least Common Multiple (LCM)
The least common multiple (LCM) of two or more integers is the smallest positive integer that is divisible by all the integers. It's a fundamental concept in number theory with applications in various fields, from simplifying fractions to solving problems in algebra and calculus. Understanding LCM is essential for working with fractions, finding common denominators, and solving problems involving periodic events.
Methods for Finding the LCM
Several methods exist for determining the LCM of numbers. Let's explore the most common approaches, focusing on their application to finding the LCM of 5 and 5.
1. Listing Multiples Method:
This is the most intuitive method, especially for smaller numbers. We list the multiples of each number until we find the smallest multiple common to both.
- Multiples of 5: 5, 10, 15, 20, 25, 30...
- Multiples of 5: 5, 10, 15, 20, 25, 30...
As you can see, the smallest multiple common to both 5 and 5 is 5. Therefore, the LCM(5, 5) = 5.
2. Prime Factorization Method:
This method is more efficient for larger numbers and provides a deeper understanding of the underlying mathematical principles. It involves finding the prime factorization of each number and then constructing the LCM using the highest powers of each prime factor present.
- Prime factorization of 5: 5 (5 is a prime number)
- Prime factorization of 5: 5 (5 is a prime number)
The prime factorization of both numbers is simply 5. Therefore, the LCM is 5.
3. Greatest Common Divisor (GCD) Method:
The LCM and GCD (greatest common divisor) of two numbers are related through the following formula:
LCM(a, b) * GCD(a, b) = a * b
First, we find the GCD of 5 and 5. Since both numbers are identical, their GCD is simply 5.
Then, we can use the formula:
LCM(5, 5) * GCD(5, 5) = 5 * 5
LCM(5, 5) * 5 = 25
LCM(5, 5) = 25 / 5 = 5
This confirms that the LCM(5, 5) = 5.
The LCM of Identical Numbers
A significant observation from the examples above is that the LCM of any number and itself is always the number itself. This is because the smallest positive integer divisible by a number is the number itself. This applies to all integers, not just 5. For example:
- LCM(7, 7) = 7
- LCM(12, 12) = 12
- LCM(100, 100) = 100
LCM and Real-World Applications
The concept of LCM is not just confined to abstract mathematical exercises. It finds practical applications in various real-world scenarios:
- Scheduling: Imagine two buses leaving a station at different intervals. The LCM can help determine when both buses will depart at the same time again.
- Fraction Addition/Subtraction: Finding the LCM of denominators is crucial for adding or subtracting fractions.
- Repeating Patterns: LCM helps identify when repeating patterns will coincide. For example, the LCM can determine when two cyclical events will occur simultaneously.
- Gear Ratios: In mechanics, gear ratios and their relationships often involve finding LCMs to determine optimal gear configurations.
Advanced LCM Calculations
For larger sets of numbers or numbers with many factors, the prime factorization method becomes increasingly efficient. Let's consider finding the LCM of three numbers: 12, 18, and 24.
-
Find the prime factorization of each number:
- 12 = 2² * 3
- 18 = 2 * 3²
- 24 = 2³ * 3
-
Identify the highest power of each prime factor:
- Highest power of 2: 2³ = 8
- Highest power of 3: 3² = 9
-
Multiply the highest powers together:
- LCM(12, 18, 24) = 8 * 9 = 72
Therefore, the LCM of 12, 18, and 24 is 72.
Frequently Asked Questions (FAQ)
Q1: What is the LCM of 0 and any other number?
A1: The LCM of 0 and any other number is undefined. This is because 0 is divisible by any number, leading to an infinite number of common multiples.
Q2: What is the LCM of two prime numbers?
A2: The LCM of two distinct prime numbers is the product of the two prime numbers. For example, LCM(2, 3) = 6.
Q3: Can the LCM of two numbers be less than both numbers?
A3: No. The LCM must be greater than or equal to the largest of the two numbers. It can only be equal if the two numbers are identical, as demonstrated with LCM(5,5)=5.
Q4: How is LCM related to GCD?
A4: The LCM and GCD are inversely related. As the GCD increases, the LCM decreases, and vice versa. Their relationship is defined by the formula: LCM(a, b) * GCD(a, b) = a * b.
Conclusion
Understanding the least common multiple is crucial for a solid foundation in mathematics. While finding the LCM of 5 and 5 is straightforward, the underlying principles and methods extend to far more complex calculations. By mastering various methods like listing multiples, prime factorization, and utilizing the relationship with GCD, you gain a comprehensive understanding of this fundamental concept and its practical applications in various fields. This knowledge empowers you to solve problems involving fractions, scheduling, and numerous other scenarios where finding common multiples is essential. Remember the key takeaway: the LCM of a number and itself is always the number itself.
Latest Posts
Latest Posts
-
To The Power Of Four
Sep 12, 2025
-
2 6 As A Percent
Sep 12, 2025
-
Whats 80 Minutes In Hours
Sep 12, 2025
-
Is 1 6 Equal To 1 3
Sep 12, 2025
-
7 Percent As A Fraction
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 5 And 5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.