Lcm Of 6 9 7
saludintensiva
Sep 13, 2025 · 6 min read
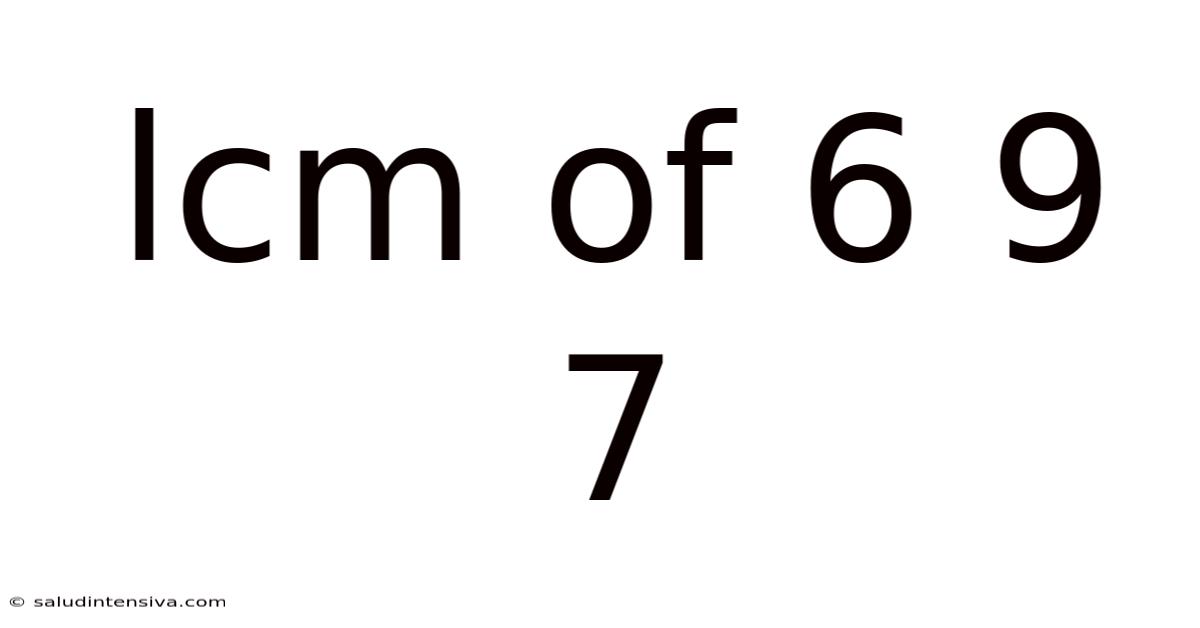
Table of Contents
Finding the Least Common Multiple (LCM) of 6, 9, and 7: A Comprehensive Guide
Finding the Least Common Multiple (LCM) might seem like a simple arithmetic task, but understanding the underlying principles and different methods for calculation is crucial for building a strong foundation in mathematics. This comprehensive guide will delve into finding the LCM of 6, 9, and 7, exploring various techniques and explaining the mathematical reasoning behind them. We'll go beyond just the answer and equip you with the tools to tackle similar problems with confidence. This article will cover the fundamental concepts of LCM, prime factorization, and the use of different methods, making it a valuable resource for students and anyone looking to refresh their math skills.
Understanding Least Common Multiple (LCM)
The Least Common Multiple (LCM) of two or more integers is the smallest positive integer that is divisible by all the integers. In simpler terms, it's the smallest number that contains all the given numbers as factors. This concept is fundamental in various mathematical applications, including simplifying fractions, solving problems involving time intervals, and understanding rhythmic patterns in music.
Let's illustrate with a simpler example. Consider finding the LCM of 2 and 3. The multiples of 2 are 2, 4, 6, 8, 10, and so on. The multiples of 3 are 3, 6, 9, 12, 15, and so on. The smallest number that appears in both lists is 6. Therefore, the LCM of 2 and 3 is 6.
Method 1: Listing Multiples
This method is straightforward, especially for smaller numbers. We list the multiples of each number until we find the smallest common multiple.
- Multiples of 6: 6, 12, 18, 24, 30, 36, 42, 54, 63, 72, 84, 90, 126, 189, 252, ...
- Multiples of 9: 9, 18, 27, 36, 45, 54, 63, 72, 81, 90, 99, 108, 117, 126, 189, 252...
- Multiples of 7: 7, 14, 21, 28, 35, 42, 49, 56, 63, 70, 77, 84, 91, 98, 105, 126, 189, 252...
By comparing the lists, we see that the smallest number appearing in all three lists is 126. Therefore, the LCM of 6, 9, and 7 is 126. However, this method becomes less efficient with larger numbers.
Method 2: Prime Factorization
Prime factorization is a more efficient and powerful method for finding the LCM, particularly for larger numbers. It involves expressing each number as a product of its prime factors. A prime number is a whole number greater than 1 that has only two divisors: 1 and itself (e.g., 2, 3, 5, 7, 11...).
Let's find the prime factorization of 6, 9, and 7:
- 6 = 2 x 3
- 9 = 3 x 3 = 3²
- 7 = 7 (7 is a prime number)
Now, to find the LCM, we take the highest power of each prime factor present in the factorizations:
- The highest power of 2 is 2¹ = 2
- The highest power of 3 is 3² = 9
- The highest power of 7 is 7¹ = 7
Multiply these highest powers together: 2 x 9 x 7 = 126. Therefore, the LCM of 6, 9, and 7 is 126. This method is more systematic and less prone to errors, especially when dealing with larger numbers.
Method 3: Greatest Common Divisor (GCD) and LCM Relationship
There's a useful relationship between the LCM and the Greatest Common Divisor (GCD) of two numbers:
LCM(a, b) x GCD(a, b) = a x b
While this formula is primarily used for two numbers, we can extend it to three numbers by finding the LCM of the LCM of two numbers and the third number. First, let's find the GCD of 6 and 9 using the prime factorization method:
- 6 = 2 x 3
- 9 = 3 x 3
The common prime factor is 3 (to the power of 1). Therefore, GCD(6, 9) = 3.
Now, let's use the formula to find the LCM(6, 9):
LCM(6, 9) x GCD(6, 9) = 6 x 9 LCM(6, 9) x 3 = 54 LCM(6, 9) = 54 / 3 = 18
Finally, we need to find the LCM of 18 and 7. Using prime factorization:
- 18 = 2 x 3²
- 7 = 7
The LCM(18, 7) = 2 x 3² x 7 = 2 x 9 x 7 = 126. This method demonstrates the interconnectedness of GCD and LCM calculations.
Visualizing LCM with Venn Diagrams
Venn diagrams can provide a visual representation of the prime factorization method. Draw three overlapping circles, one for each number (6, 9, 7). Inside each circle, write its prime factors:
- Circle 6: 2, 3
- Circle 9: 3, 3
- Circle 7: 7
The LCM is obtained by multiplying the unique prime factors, taking the highest power where applicable. In this case, it's 2 x 3 x 3 x 7 = 126. This visual approach can be helpful for understanding the concept and for students who prefer visual learning.
Applications of LCM
The concept of LCM has numerous applications in various fields:
- Fraction Addition and Subtraction: Finding a common denominator when adding or subtracting fractions requires finding the LCM of the denominators.
- Scheduling Problems: Determining when events will occur simultaneously, such as buses arriving at a stop or machines completing cycles, involves finding the LCM of the time intervals.
- Rhythmic Patterns: In music, LCM is used to determine when rhythmic patterns repeat simultaneously.
- Gear Ratios: In mechanics, gear ratios often involve LCM calculations to determine the optimal gear combinations.
- Modular Arithmetic: LCM plays a crucial role in understanding modular arithmetic, which is used in cryptography and other areas of mathematics.
Frequently Asked Questions (FAQ)
Q: What if the numbers have no common factors?
A: If the numbers are relatively prime (meaning they share no common factors other than 1), their LCM is simply their product. For example, the LCM of 5 and 7 is 5 x 7 = 35.
Q: Can I use a calculator to find the LCM?
A: Many scientific calculators have built-in functions to calculate the LCM. However, understanding the underlying methods is essential for solving more complex problems and for developing a deeper understanding of number theory.
Q: Is there a formula for finding the LCM of more than three numbers?
A: Yes, the prime factorization method can be extended to any number of integers. Find the prime factorization of each number, then take the highest power of each prime factor present in any of the factorizations and multiply them together.
Q: Why is understanding LCM important?
A: Understanding LCM is crucial for developing strong foundational skills in mathematics. It’s a fundamental concept that applies to various areas of mathematics and its applications in other fields. It helps develop problem-solving skills and analytical thinking.
Conclusion
Finding the LCM of 6, 9, and 7, as demonstrated through multiple methods, highlights the versatility and importance of understanding number theory concepts. While the answer (126) is readily obtained, the journey of exploring different approaches – listing multiples, prime factorization, and the LCM-GCD relationship – provides a deeper understanding of the underlying mathematical principles. Mastering LCM calculation enhances your mathematical abilities and opens doors to more advanced mathematical concepts and their real-world applications. Remember to practice with different numbers to solidify your understanding and build confidence in tackling similar problems.
Latest Posts
Latest Posts
-
Gcf Of 8 And 5
Sep 13, 2025
-
Is 1 4 Bigger Than 5 8
Sep 13, 2025
-
36 50 As A Percent
Sep 13, 2025
-
10 3 As A Fraction
Sep 13, 2025
-
What Time Is 13 55
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 6 9 7 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.