Lcm Of 7 And 13
saludintensiva
Sep 13, 2025 · 6 min read
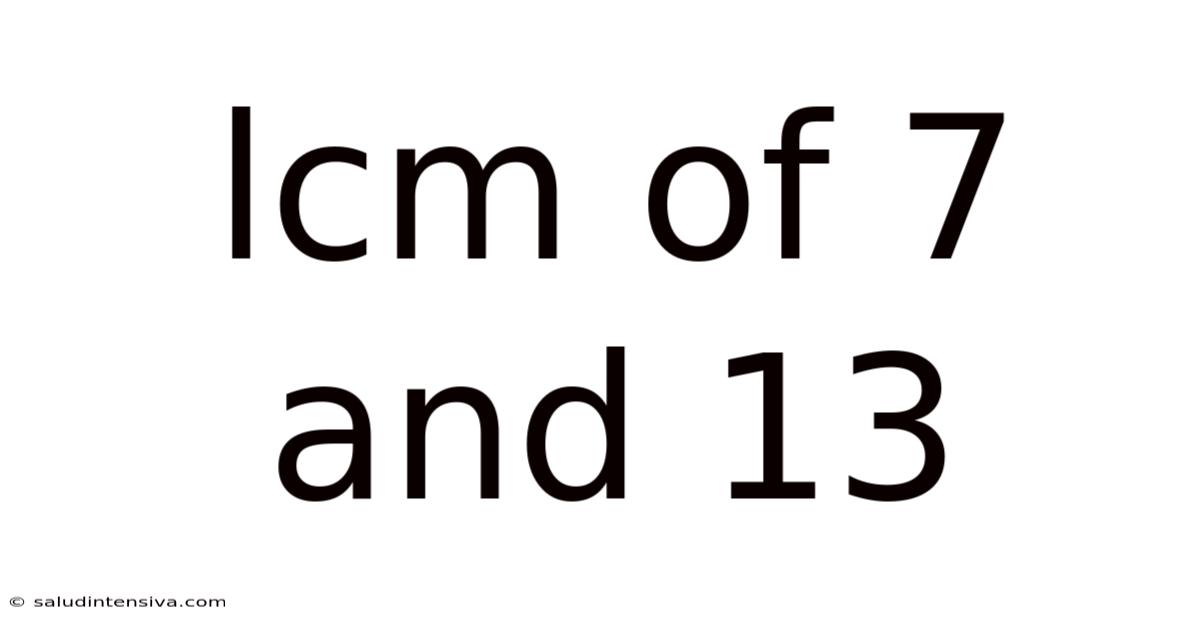
Table of Contents
Unveiling the Least Common Multiple (LCM) of 7 and 13: A Deep Dive into Number Theory
Finding the least common multiple (LCM) of two numbers might seem like a simple arithmetic task, but it underpins a significant portion of number theory and has practical applications in various fields, from scheduling to music theory. This article will explore the LCM of 7 and 13 in detail, providing not only the solution but also a comprehensive understanding of the underlying concepts and methods. We'll delve into different approaches to finding the LCM, examine the prime factorization method, and discuss the relationship between LCM and the greatest common divisor (GCD). Understanding LCMs is key to mastering fractions, simplifying expressions, and solving various mathematical problems.
Understanding Least Common Multiple (LCM)
The least common multiple (LCM) of two or more integers is the smallest positive integer that is divisible by all the integers. Think of it as the smallest number that contains all the given numbers as factors. For example, the LCM of 2 and 3 is 6 because 6 is the smallest number that is divisible by both 2 and 3.
In contrast to the greatest common divisor (GCD), which finds the largest number that divides all given numbers without leaving a remainder, the LCM searches for the smallest number that is a multiple of all given numbers. Both concepts are fundamental in number theory and are closely related, as we'll explore later.
Methods for Finding the LCM of 7 and 13
There are several methods to determine the LCM of two numbers. Let's explore the most common ones and apply them to find the LCM of 7 and 13.
1. Listing Multiples Method:
This is a straightforward method, especially for smaller numbers. We list the multiples of each number until we find the smallest common multiple.
- Multiples of 7: 7, 14, 21, 28, 35, 42, 49, 56, 63, 70, 77, 84, 91, 98, 105, 112, 119, 126, 133, 140, 147, 154, 161, 168, 175, 182, 189, 196, 203, 210...
- Multiples of 13: 13, 26, 39, 52, 65, 78, 91, 104, 117, 130, 143, 156, 169, 182, 195, 208, 221, 234, 247, 260...
By comparing the lists, we observe that the smallest common multiple is 91. Therefore, the LCM(7, 13) = 91.
This method is effective for small numbers, but it becomes less practical as the numbers increase in size.
2. Prime Factorization Method:
This is a more efficient method, particularly for larger numbers. It involves finding the prime factorization of each number and then constructing the LCM using the highest powers of each prime factor present.
- Prime factorization of 7: 7 is a prime number, so its prime factorization is simply 7.
- Prime factorization of 13: 13 is also a prime number, so its prime factorization is 13.
Since 7 and 13 are both prime and distinct, their LCM is simply their product.
Therefore, LCM(7, 13) = 7 × 13 = 91.
This method is elegant and efficient, regardless of the size of the numbers. It provides a systematic approach to finding the LCM and is widely applicable.
3. Using the Formula: LCM(a, b) = (|a × b|) / GCD(a, b)
This method leverages the relationship between the LCM and the GCD of two numbers. The formula states that the LCM of two numbers (a and b) is equal to the absolute value of their product divided by their greatest common divisor.
First, we need to find the GCD of 7 and 13. Since 7 and 13 are both prime numbers and have no common factors other than 1, their GCD is 1.
Now, we can apply the formula:
LCM(7, 13) = (|7 × 13|) / GCD(7, 13) = 91 / 1 = 91
This method highlights the inherent connection between LCM and GCD. It's particularly useful when dealing with larger numbers where finding the GCD first can simplify the calculation.
The Significance of Prime Factorization in Finding LCM
The prime factorization method is crucial for understanding the fundamental structure of numbers and their relationships. Prime numbers are the building blocks of all integers, and their factorization provides insights into divisibility and multiples.
By expressing each number as a product of its prime factors, we can systematically identify the common factors and the unique factors. The LCM is then constructed by taking the highest power of each prime factor present in the factorizations of the given numbers. This method is not only efficient but also provides a deep understanding of the mathematical properties involved.
Applications of LCM
The concept of LCM has wide-ranging applications in various fields:
-
Scheduling: Determining when events will occur simultaneously. For example, if two buses arrive at a stop every 7 and 13 minutes respectively, the LCM helps calculate when they'll arrive together. In this case, they'll arrive together every 91 minutes.
-
Music Theory: Finding the least common multiple of the durations of different musical notes to determine the shortest duration that encompasses a whole number of beats for each note.
-
Fractions: Finding a common denominator when adding or subtracting fractions. The LCM of the denominators serves as the least common denominator, simplifying the calculation.
-
Modular Arithmetic: Used in cryptography and other areas of mathematics. LCM is essential in solving congruence equations.
Frequently Asked Questions (FAQ)
Q: What if one of the numbers is 0?
A: The LCM of any number and 0 is undefined. 0 is a multiple of every number, so there is no smallest positive multiple common to both.
Q: Can the LCM of two numbers be equal to one of the numbers?
A: Yes, if one number is a multiple of the other. For example, LCM(4, 8) = 8.
Q: Is there a shortcut to find the LCM of two numbers if they are coprime (their GCD is 1)?
A: Yes, if two numbers are coprime, their LCM is simply their product. This is the case with 7 and 13, as their GCD is 1, and their LCM is 7 * 13 = 91.
Q: How do I find the LCM of more than two numbers?
A: You can extend the prime factorization method. Find the prime factorization of each number, and then take the highest power of each prime factor present in any of the factorizations to construct the LCM. Alternatively, you can find the LCM of two numbers, then find the LCM of the result and the next number, and so on.
Q: What is the relationship between LCM and GCD?
A: The LCM and GCD of two numbers a and b are related by the equation: LCM(a, b) * GCD(a, b) = |a * b|. This relationship provides a powerful tool for calculating either LCM or GCD if the other is known.
Conclusion
Finding the LCM of 7 and 13, which is 91, is a straightforward exercise that illustrates fundamental concepts in number theory. While the simple listing method works for small numbers, the prime factorization method provides a more robust and efficient approach, particularly for larger numbers. Understanding the LCM and its relationship with the GCD is crucial for solving various mathematical problems and has practical applications in numerous fields. This exploration goes beyond simply finding the answer; it offers a deeper appreciation of the underlying mathematical principles and their significance. Remember, the seemingly simple act of finding the LCM opens doors to a deeper understanding of number theory and its practical implications.
Latest Posts
Latest Posts
-
11 Out Of 25 Percentage
Sep 13, 2025
-
53 5 As A Decimal
Sep 13, 2025
-
23 6 As A Decimal
Sep 13, 2025
-
What Is 4 5 In Fraction
Sep 13, 2025
-
55 Percent As A Decimal
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 7 And 13 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.