Lcm Of 9 And 18
saludintensiva
Sep 18, 2025 · 6 min read
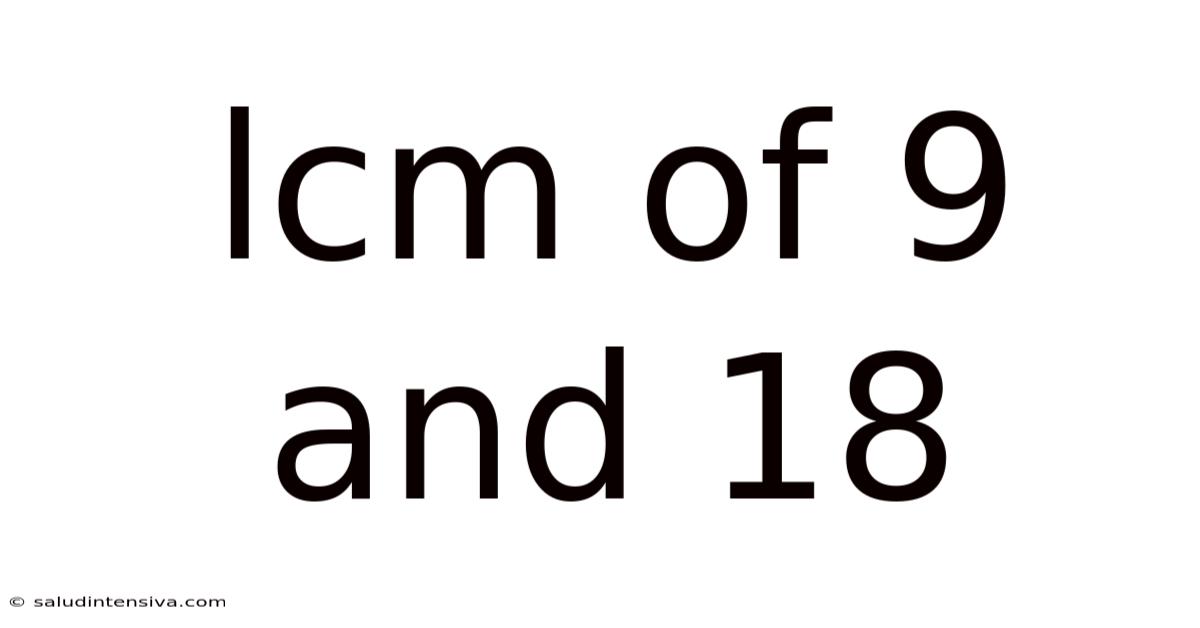
Table of Contents
Finding the LCM of 9 and 18: A Deep Dive into Least Common Multiples
Finding the least common multiple (LCM) of two numbers, like 9 and 18, might seem like a simple task, especially for those familiar with basic arithmetic. However, understanding the underlying concepts and various methods for calculating the LCM provides a valuable foundation in mathematics, crucial for tackling more complex problems in algebra, number theory, and beyond. This article delves into the intricacies of finding the LCM of 9 and 18, exploring multiple approaches and explaining the mathematical principles involved. We'll also uncover why understanding LCM is essential, not just for school assignments, but for practical applications in everyday life.
Understanding Least Common Multiples (LCM)
Before we jump into calculating the LCM of 9 and 18, let's solidify our understanding of what an LCM actually is. The least common multiple of two or more integers is the smallest positive integer that is a multiple of all the integers. In simpler terms, it's the smallest number that both (or all) the numbers divide into evenly.
Think of it like this: imagine you have two gears with different numbers of teeth. The LCM represents the smallest number of rotations needed for both gears to return to their starting positions simultaneously. This analogy illustrates the practical relevance of LCM in fields like engineering and mechanics.
Method 1: Listing Multiples
This is a straightforward method, particularly useful for smaller numbers. We list the multiples of each number until we find the smallest multiple common to both.
- Multiples of 9: 9, 18, 27, 36, 45, 54, ...
- Multiples of 18: 18, 36, 54, 72, ...
Notice that the smallest number appearing in both lists is 18. Therefore, the LCM of 9 and 18 is 18. This method works well for small numbers but becomes increasingly cumbersome as the numbers get larger.
Method 2: Prime Factorization
Prime factorization is a more efficient and powerful method, especially for larger numbers. This method involves breaking down each number into its prime factors – numbers divisible only by 1 and themselves.
- Prime Factorization of 9: 9 = 3 x 3 = 3²
- Prime Factorization of 18: 18 = 2 x 3 x 3 = 2 x 3²
Now, to find the LCM, we take the highest power of each prime factor present in the factorizations:
- The highest power of 2 is 2¹ (from the factorization of 18).
- The highest power of 3 is 3² (from both factorizations).
Multiplying these highest powers together gives us the LCM: 2¹ x 3² = 2 x 9 = 18.
Therefore, the LCM of 9 and 18, using prime factorization, is 18. This method is far more efficient than listing multiples when dealing with larger numbers, as it provides a systematic approach to finding the LCM.
Method 3: Using the Greatest Common Divisor (GCD)
The LCM and the greatest common divisor (GCD) are intimately related. The GCD is the largest number that divides both numbers evenly. There's a handy formula connecting the LCM and GCD:
LCM(a, b) = (a x b) / GCD(a, b)
where 'a' and 'b' are the two numbers.
Let's find the GCD of 9 and 18 first. The factors of 9 are 1, 3, and 9. The factors of 18 are 1, 2, 3, 6, 9, and 18. The greatest common factor is 9.
Now, applying the formula:
LCM(9, 18) = (9 x 18) / GCD(9, 18) = (9 x 18) / 9 = 18
This method highlights the interconnectedness of LCM and GCD, offering an alternative approach to calculating the LCM.
Why is Finding the LCM Important?
Understanding and calculating LCM isn't just an academic exercise; it has practical applications across numerous fields:
-
Scheduling: Imagine you have two events that occur at regular intervals. The LCM helps determine when both events will coincide again. For example, if one event happens every 9 days and another every 18 days, they'll coincide every 18 days (the LCM of 9 and 18).
-
Fractions: Finding the LCM is crucial when adding or subtracting fractions with different denominators. You need to find the LCM of the denominators to create a common denominator, simplifying the addition or subtraction process.
-
Measurement: In construction or engineering, the LCM helps find the smallest common length or unit for consistent measurements. Imagine needing to cut pieces of wood measuring 9cm and 18cm; using the LCM (18cm) ensures efficient use of material.
-
Music Theory: The LCM is used in music to determine the least common multiple of note durations, which helps in rhythmic coordination.
-
Computer Science: In various algorithms and programming tasks, the concept of LCM is applied in optimizing processes and ensuring synchronization.
-
Everyday Life: Many everyday problems, even seemingly unrelated to mathematics, can be efficiently solved using the LCM. For instance, coordinating meeting times with people with varying work schedules requires understanding of least common multiples.
Advanced Concepts and Extensions
The methods described above can be extended to find the LCM of more than two numbers. For instance, to find the LCM of 9, 18, and 27, we would again employ prime factorization.
-
Prime Factorization:
- 9 = 3²
- 18 = 2 x 3²
- 27 = 3³
-
Identifying Highest Powers:
- Highest power of 2: 2¹
- Highest power of 3: 3³
-
Calculating LCM:
- LCM(9, 18, 27) = 2¹ x 3³ = 2 x 27 = 54
The LCM of 9, 18, and 27 is 54.
Frequently Asked Questions (FAQ)
Q: What if the two numbers are relatively prime (their GCD is 1)?
A: If the GCD of two numbers is 1, then their LCM is simply the product of the two numbers. For example, the LCM of 9 and 5 (which are relatively prime) is 9 x 5 = 45.
Q: Can I use a calculator to find the LCM?
A: Yes, many scientific calculators have a built-in function to calculate the LCM of two or more numbers. However, understanding the underlying methods is crucial for grasping the mathematical concepts and solving more complex problems.
Q: Is there a limit to the size of numbers for which I can find the LCM?
A: Theoretically, there's no limit. However, for extremely large numbers, computational power might become a constraint. The prime factorization method, while efficient, can become computationally intensive for extremely large numbers that are difficult to factor.
Q: Why is prime factorization so important in finding the LCM?
A: Prime factorization provides a fundamental building block approach. By breaking down numbers into their prime factors, we systematically account for all the divisors, ensuring we find the smallest number that contains all the necessary factors to be a multiple of both (or all) original numbers.
Conclusion
Finding the LCM of 9 and 18, while seemingly simple, serves as a gateway to understanding fundamental mathematical concepts with broader applications. This article demonstrated multiple methods – listing multiples, prime factorization, and using the GCD – highlighting the interconnectedness of these mathematical ideas. Mastering these techniques not only equips you to solve LCM problems efficiently but also strengthens your overall mathematical foundation, proving invaluable in various academic and real-world scenarios. Remember that the key lies not just in the answer (which is 18 in this case), but in understanding the why behind the methods, empowering you to tackle more complex problems with confidence and proficiency.
Latest Posts
Latest Posts
-
How Tall Is Two Meters
Sep 18, 2025
-
3 And 1 2 In
Sep 18, 2025
-
11 20 As A Decimal
Sep 18, 2025
-
How Many Days Till March
Sep 18, 2025
-
16 20 As A Decimal
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 9 And 18 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.