Negative 3 Minus Negative 6
saludintensiva
Sep 24, 2025 · 5 min read
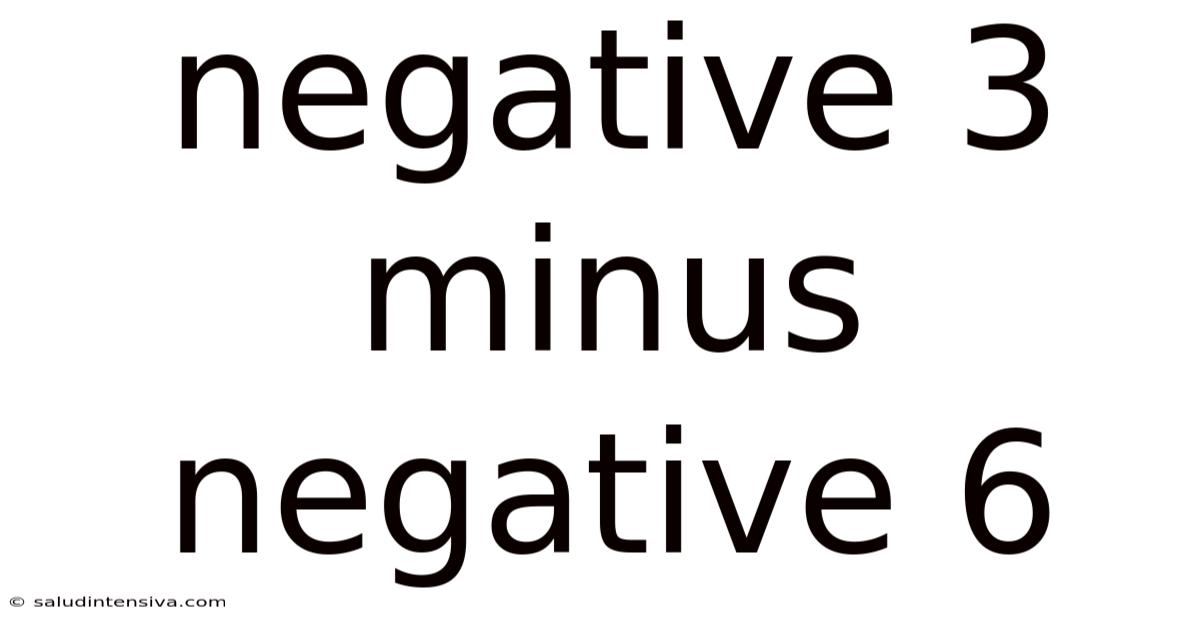
Table of Contents
Decoding the Mystery: Negative 3 Minus Negative 6
Understanding negative numbers can be tricky, especially when dealing with subtraction. Many students struggle with problems like "-3 - (-6)". This seemingly simple equation holds the key to understanding fundamental concepts in algebra and arithmetic. This article will comprehensively explore the solution to "-3 - (-6)", providing a step-by-step explanation, delving into the underlying mathematical principles, and addressing common misconceptions. By the end, you'll not only know the answer but also possess a deeper understanding of how to tackle similar problems confidently.
Introduction: Understanding Negative Numbers and Subtraction
Before diving into the problem, let's establish a strong foundation. Negative numbers represent values less than zero. They're often used to represent things like debt, temperatures below freezing, or positions below sea level. Subtraction, in its simplest form, means taking away a quantity. However, when dealing with negative numbers, the process becomes slightly more nuanced. The key to understanding subtraction with negative numbers lies in grasping the concept of opposites.
Step-by-Step Solution: -3 - (-6)
Let's break down the equation "-3 - (-6)" step-by-step:
-
Recognizing the Double Negative: The core of this problem lies in the expression "-(-6)". A double negative, in mathematics, translates to a positive. Think of it like this: if you owe someone six dollars (represented by -6), and then that debt is removed (-(-6)), it's equivalent to gaining six dollars.
-
Simplifying the Expression: Replacing "-(-6)" with "+6", our equation now becomes: -3 + 6.
-
Performing the Addition: Now we have a simple addition problem. Starting at -3 on the number line, we move six units to the right (positive direction).
-
The Solution: This leads us to the final answer: 3. Therefore, -3 - (-6) = 3.
Visualizing with the Number Line
A number line is a powerful tool for visualizing mathematical operations, especially those involving negative numbers. Let's illustrate the solution on a number line:
-
Start at -3: Place a marker at -3 on the number line.
-
Subtract -6 (or add +6): Since subtracting a negative is the same as adding a positive, we move six units to the right from -3.
-
Arrive at 3: After moving six units to the right, our marker ends up at 3.
The Mathematical Principles: Additive Inverse and Subtraction as Addition
The solution to "-3 - (-6)" relies on two important mathematical concepts:
-
Additive Inverse: Every number has an additive inverse. The additive inverse of a number is the number that, when added to the original number, results in zero. For example, the additive inverse of -6 is +6, and the additive inverse of 3 is -3.
-
Subtraction as Addition: Subtraction can be viewed as adding the additive inverse. Therefore, "a - b" is equivalent to "a + (-b)". This concept is crucial when working with negative numbers. The expression "-3 - (-6)" can be rewritten as "-3 + (+6)", making the calculation much clearer.
Expanding the Understanding: More Complex Examples
Once you grasp the fundamental principle of the double negative and subtraction as addition, you can tackle more complex problems involving negative numbers. Consider these examples:
-
-5 - (-2): This simplifies to -5 + 2 = -3.
-
-8 - (-10): This simplifies to -8 + 10 = 2.
-
-12 - (-5) - (-3): This simplifies to -12 + 5 + 3 = -4.
In each example, the key is to recognize the double negative and rewrite the subtraction as the addition of the additive inverse.
Addressing Common Misconceptions
Several common misconceptions can arise when dealing with negative numbers and subtraction:
-
Ignoring the Double Negative: Many students mistakenly subtract the numbers without considering the double negative. Remembering that "-(-x) = x" is crucial.
-
Confusing Addition and Subtraction: The rules for adding and subtracting negative numbers are different from those for positive numbers. Understanding the concept of additive inverse helps clarify this.
-
Incorrect Number Line Visualization: Students may incorrectly move left instead of right when subtracting a negative number. Careful visualization on the number line can alleviate this.
Frequently Asked Questions (FAQ)
Q1: Why does a double negative become a positive?
A1: Subtracting a number is equivalent to adding its opposite. When you subtract a negative number, you're adding its positive counterpart.
Q2: Can I always rewrite subtraction as addition?
A2: Yes, you can always rewrite a subtraction problem as an addition problem by adding the additive inverse of the number being subtracted.
Q3: What if I have more than two negative numbers in a subtraction problem?
A3: Deal with each double negative individually, simplifying the expression step-by-step. Remember to always convert subtractions to additions of additive inverses.
Q4: How can I practice more problems involving negative numbers?
A4: You can find numerous practice problems in algebra textbooks, online math resources, and educational websites. Start with simple problems and gradually increase the complexity.
Conclusion: Mastering Negative Number Subtraction
Understanding negative number subtraction is a crucial skill in mathematics. By grasping the concepts of additive inverse and viewing subtraction as the addition of the opposite, you can confidently tackle any problem involving negative numbers. The key takeaway is to remember that "-(-x) = x" and practice consistently to build proficiency. This improved understanding will serve as a strong foundation for more advanced mathematical concepts in algebra and beyond. Don't hesitate to use the number line as a visual aid to better understand the processes involved. With consistent practice and a clear understanding of the principles, you'll master negative number subtraction with ease.
Latest Posts
Latest Posts
-
Use Excel To Calculate Age
Sep 24, 2025
-
Unit For Coefficient Of Friction
Sep 24, 2025
-
Find Equation Of Parallel Line
Sep 24, 2025
-
How To Pronounce Large Numbers
Sep 24, 2025
-
Unit Weight Of Water English
Sep 24, 2025
Related Post
Thank you for visiting our website which covers about Negative 3 Minus Negative 6 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.