Negative 5 Minus Negative 7
saludintensiva
Sep 16, 2025 · 5 min read
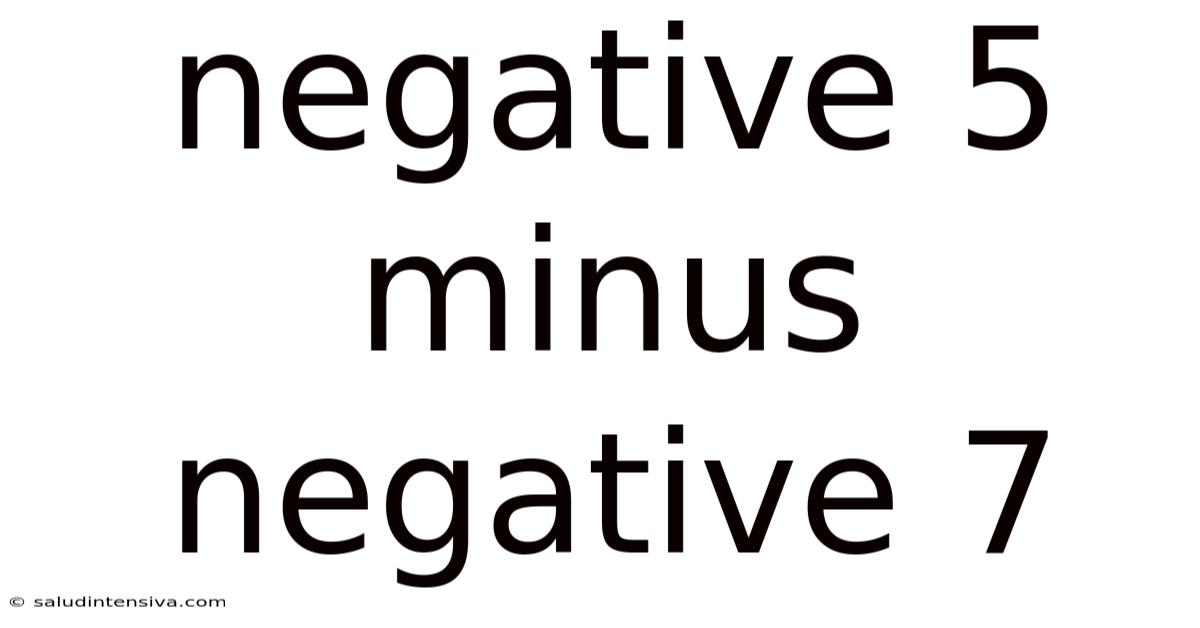
Table of Contents
Decoding the Mystery: Negative 5 Minus Negative 7
Understanding negative numbers can often feel like navigating a tricky maze. This article will unravel the seemingly complex calculation of -5 - (-7), explaining not only the answer but also the underlying principles of integer arithmetic, providing a solid foundation for more advanced mathematical concepts. We’ll explore the rules of subtracting negative numbers, offer visual representations to aid comprehension, and address frequently asked questions. By the end, you'll confidently tackle similar problems and appreciate the elegance of mathematical operations.
Introduction: Understanding Negative Numbers and Subtraction
Before diving into -5 - (-7), let's establish a firm grasp of negative numbers and subtraction. Negative numbers represent values less than zero, often visualized on a number line extending to the left of zero. Subtraction, fundamentally, is the process of taking away or finding the difference between two numbers. When dealing with negative numbers, the process might seem counterintuitive at first, but with a systematic approach, it becomes straightforward.
Think of a number line. Zero is the midpoint. Positive numbers extend to the right, while negative numbers extend to the left. Subtraction on the number line means moving to the left. Adding a positive number means moving to the right. Adding a negative number (which is the same as subtracting a positive number) means moving to the left. Subtracting a negative number means moving to the right.
Step-by-Step Solution: -5 - (-7)
Let's break down the calculation -5 - (-7) step-by-step:
-
Understanding the Double Negative: The core of this problem lies in understanding the double negative: -(-7). Two negative signs next to each other cancel each other out, resulting in a positive value. Therefore, -(-7) becomes +7.
-
Rewrite the Equation: Our equation now transforms from -5 - (-7) to -5 + 7.
-
Performing the Addition: We now have a simple addition problem: -5 + 7. We can visualize this on a number line. Start at -5. Adding 7 means moving 7 units to the right. This lands us at +2.
Therefore, -5 - (-7) = 2
Visual Representation: The Number Line Approach
A number line offers a powerful visual aid for understanding this type of calculation.
- Start at -5: Locate -5 on the number line.
- Subtracting a negative: Subtracting a negative number is equivalent to adding its positive counterpart. So, subtracting -7 is the same as adding +7.
- Move 7 units to the right: From -5, move 7 units to the right along the number line.
- Arrive at 2: You will land on the number 2. This visually confirms that -5 - (-7) = 2.
The Mathematical Principle: Additive Inverse
The solution hinges on the concept of the additive inverse. The additive inverse of a number is the number that, when added to the original number, results in zero. For example, the additive inverse of 7 is -7 (7 + (-7) = 0), and the additive inverse of -7 is 7 (-7 + 7 = 0).
When we subtract a number, we are essentially adding its additive inverse. So, subtracting -7 is the same as adding +7. This principle is crucial for understanding operations with negative numbers.
Expanding the Concept: More Complex Examples
Let's extend our understanding to more complex scenarios involving negative numbers and subtraction:
-
Example 1: -12 - (-5): Following the same principles, this simplifies to -12 + 5. Starting at -12 on the number line and moving 5 units to the right, we arrive at -7. Therefore, -12 - (-5) = -7.
-
Example 2: -3 - (-8) - (-2): This equation becomes -3 + 8 + 2. Working from left to right: -3 + 8 = 5, and 5 + 2 = 7. Therefore, -3 - (-8) - (-2) = 7.
-
Example 3: 10 - (-4) - 6: This simplifies to 10 + 4 - 6. 10 + 4 = 14, and 14 - 6 = 8. Therefore, 10 - (-4) - 6 = 8.
These examples highlight the consistency of the rules governing subtraction of negative numbers. The key is always to remember that subtracting a negative number is equivalent to adding its positive counterpart.
Frequently Asked Questions (FAQ)
Q1: Why does subtracting a negative number result in addition?
A1: Subtracting a number is the opposite of adding it. Since subtracting -7 is the opposite of adding -7, it's equivalent to adding +7 (its additive inverse). This is a fundamental property of integer arithmetic.
Q2: Can I use a calculator for these types of problems?
A2: Yes, most calculators will correctly handle negative numbers and subtraction. However, understanding the underlying principles is essential for problem-solving and building a strong mathematical foundation.
Q3: What if I have more than two negative numbers in a subtraction problem?
A3: Address each double negative individually. For example, in -5 - (-3) - (-2), simplify -(-3) to +3 and -(-2) to +2. The equation then becomes -5 + 3 + 2 = 0.
Q4: Are there any real-world applications of this concept?
A4: Absolutely! Many real-world situations involve negative numbers, such as debt (-$100), temperature (-10°C), or changes in elevation (-50 meters). Understanding how to subtract negative numbers is crucial for accurately calculating changes and differences in these scenarios.
Conclusion: Mastering Negative Numbers
Understanding the subtraction of negative numbers, as exemplified by the problem -5 - (-7), is a fundamental skill in mathematics. By mastering the concept of the additive inverse and visualizing the process on a number line, you can confidently solve similar problems. This understanding lays the groundwork for more advanced mathematical concepts and problem-solving in various fields. Remember the key takeaway: subtracting a negative is the same as adding a positive. With practice, these concepts will become second nature, enabling you to navigate the world of numbers with greater ease and confidence. Don't be afraid to practice; the more you work with negative numbers, the more intuitive these operations will become.
Latest Posts
Latest Posts
-
9 Divided By 1 3
Sep 16, 2025
-
6 5 8 As A Decimal
Sep 16, 2025
-
48 Hours Is How Long
Sep 16, 2025
-
7 5 As A Mixed Number
Sep 16, 2025
-
14 Percent As A Decimal
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about Negative 5 Minus Negative 7 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.