Simplest Form Of 12 16
saludintensiva
Sep 12, 2025 · 6 min read
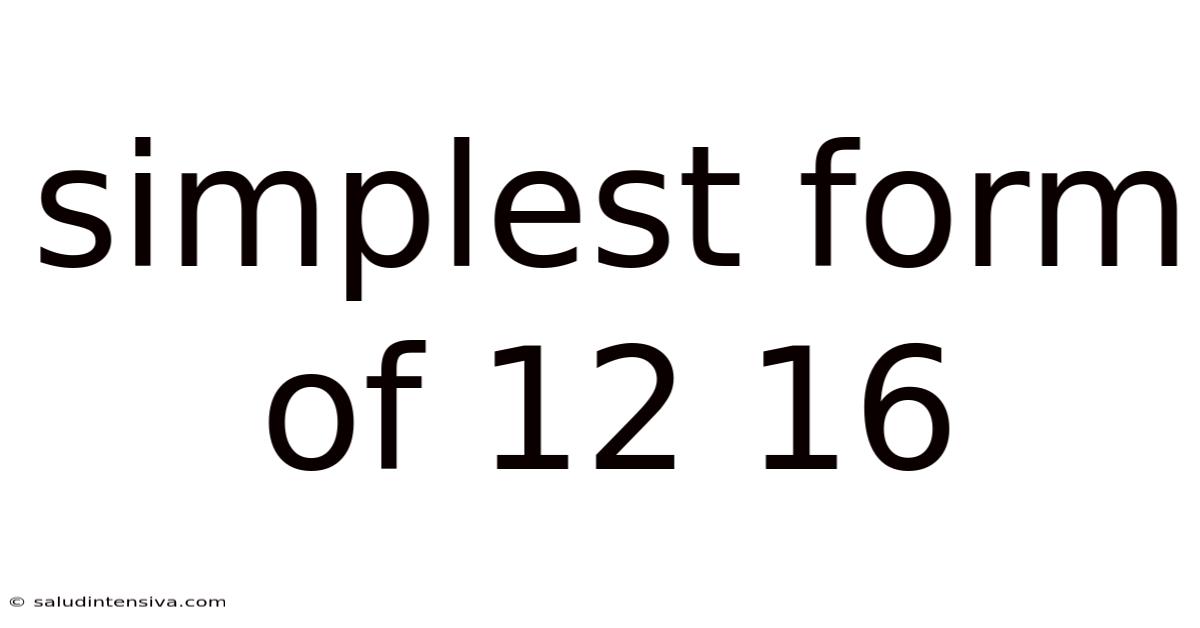
Table of Contents
Finding the Simplest Form of a Fraction: A Deep Dive into 12/16
Finding the simplest form of a fraction is a fundamental concept in mathematics. It's a skill crucial for understanding ratios, proportions, and various other mathematical concepts. This article will guide you through the process of simplifying fractions, using the example of 12/16, and explore the underlying mathematical principles. We'll cover different methods, address common misconceptions, and even delve into the reasons why simplifying fractions is so important. By the end, you'll not only know how to simplify 12/16 but also have a solid understanding of the concept applicable to any fraction.
Understanding Fractions: A Quick Refresher
Before we dive into simplifying 12/16, let's briefly review what a fraction represents. A fraction is a part of a whole. It's expressed as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). The numerator indicates how many parts we have, and the denominator indicates how many equal parts the whole is divided into. For example, in the fraction 12/16, 12 represents the number of parts we have, and 16 represents the total number of equal parts the whole is divided into.
Method 1: Finding the Greatest Common Divisor (GCD)
The most efficient way to simplify a fraction is by finding the greatest common divisor (GCD) of the numerator and the denominator. The GCD is the largest number that divides both the numerator and the denominator without leaving a remainder. Once we find the GCD, we divide both the numerator and the denominator by it to obtain the simplest form.
Let's apply this to 12/16:
- Find the factors of 12: 1, 2, 3, 4, 6, 12
- Find the factors of 16: 1, 2, 4, 8, 16
- Identify the common factors: 1, 2, 4
- Determine the greatest common factor (GCF): The largest common factor is 4.
Now, we divide both the numerator and the denominator by the GCD (4):
12 ÷ 4 = 3 16 ÷ 4 = 4
Therefore, the simplest form of 12/16 is 3/4.
Method 2: Successive Division by Common Factors
If you don't immediately see the GCD, you can simplify the fraction by successively dividing the numerator and denominator by common factors until no common factors remain. This method might take more steps but is still effective.
Let's simplify 12/16 using this method:
-
Notice that both 12 and 16 are even numbers, so we can divide both by 2: 12 ÷ 2 = 6 16 ÷ 2 = 8 This gives us the fraction 6/8.
-
Now, we notice that both 6 and 8 are still even, so we can again divide by 2: 6 ÷ 2 = 3 8 ÷ 2 = 4 This gives us the fraction 3/4.
Since 3 and 4 have no common factors other than 1, we've reached the simplest form. Again, the simplest form of 12/16 is 3/4.
Method 3: Prime Factorization
Prime factorization is a powerful technique for finding the GCD. It involves expressing each number as a product of its prime factors. The GCD is then found by multiplying the common prime factors raised to the lowest power.
Let's find the simplest form of 12/16 using prime factorization:
- Prime factorization of 12: 2 x 2 x 3 (2² x 3)
- Prime factorization of 16: 2 x 2 x 2 x 2 (2⁴)
- Identify common prime factors: The only common prime factor is 2.
- Determine the lowest power of the common prime factor: The lowest power of 2 is 2².
- Calculate the GCD: The GCD is 2² = 4.
Now, we divide both the numerator and the denominator by the GCD (4):
12 ÷ 4 = 3 16 ÷ 4 = 4
Once again, the simplest form of 12/16 is 3/4.
Why Simplifying Fractions is Important
Simplifying fractions is more than just a mathematical exercise; it has practical implications:
-
Clarity and Understanding: Simplified fractions are easier to understand and interpret. 3/4 is much clearer than 12/16. It immediately tells us that we have three parts out of four equal parts.
-
Easier Calculations: Simplifying fractions makes subsequent calculations much simpler. Multiplying or dividing fractions is significantly easier when they are in their simplest form.
-
Comparison: It’s easier to compare fractions when they are simplified. For example, comparing 3/4 and 5/8 is much simpler than comparing 12/16 and 5/8.
-
Real-world Applications: Simplifying fractions is crucial in various real-world applications, such as cooking (measuring ingredients), construction (measuring materials), and finance (calculating proportions).
Common Mistakes to Avoid
-
Dividing by a number that is not a common factor: Ensure that you are dividing both the numerator and the denominator by a number that divides both evenly without leaving a remainder.
-
Not finding the greatest common divisor: If you don't find the GCD, you'll end up with a simplified fraction, but it won't be in its simplest form.
-
Incorrect prime factorization: Make sure you correctly identify the prime factors of the numbers.
Frequently Asked Questions (FAQ)
Q: Is there a way to simplify fractions without finding the GCD?
A: While finding the GCD is the most efficient method, you can simplify by successively dividing by common factors, as shown in Method 2. This might require more steps but still leads to the correct answer.
Q: Can I simplify a fraction by only dividing the numerator or the denominator?
A: No, you must divide both the numerator and the denominator by the same number to maintain the value of the fraction. Dividing only the numerator or denominator changes the fraction's value.
Q: What if the numerator is larger than the denominator?
A: This is an improper fraction. You can simplify it the same way you simplify a proper fraction (numerator smaller than denominator). You can also convert it into a mixed number, which is a combination of a whole number and a proper fraction.
Q: What if the numerator and denominator have no common factors other than 1?
A: The fraction is already in its simplest form.
Conclusion
Simplifying fractions is a crucial skill in mathematics with broad applications. While several methods exist, understanding the concept of the greatest common divisor (GCD) provides the most efficient approach. Remember to always divide both the numerator and the denominator by the GCD to arrive at the simplest form. By mastering this fundamental skill, you'll build a strong foundation for more advanced mathematical concepts and confidently tackle various real-world problems involving fractions. Through understanding the methods and avoiding common pitfalls, you'll become proficient in simplifying fractions, ensuring accurate and efficient calculations in any context. The example of 12/16, simplified to 3/4, beautifully illustrates the simplicity and elegance of this fundamental mathematical process.
Latest Posts
Latest Posts
-
To The Power Of Four
Sep 12, 2025
-
2 6 As A Percent
Sep 12, 2025
-
Whats 80 Minutes In Hours
Sep 12, 2025
-
Is 1 6 Equal To 1 3
Sep 12, 2025
-
7 Percent As A Fraction
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about Simplest Form Of 12 16 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.