Simplify Each Fraction 2 16
saludintensiva
Sep 18, 2025 · 6 min read
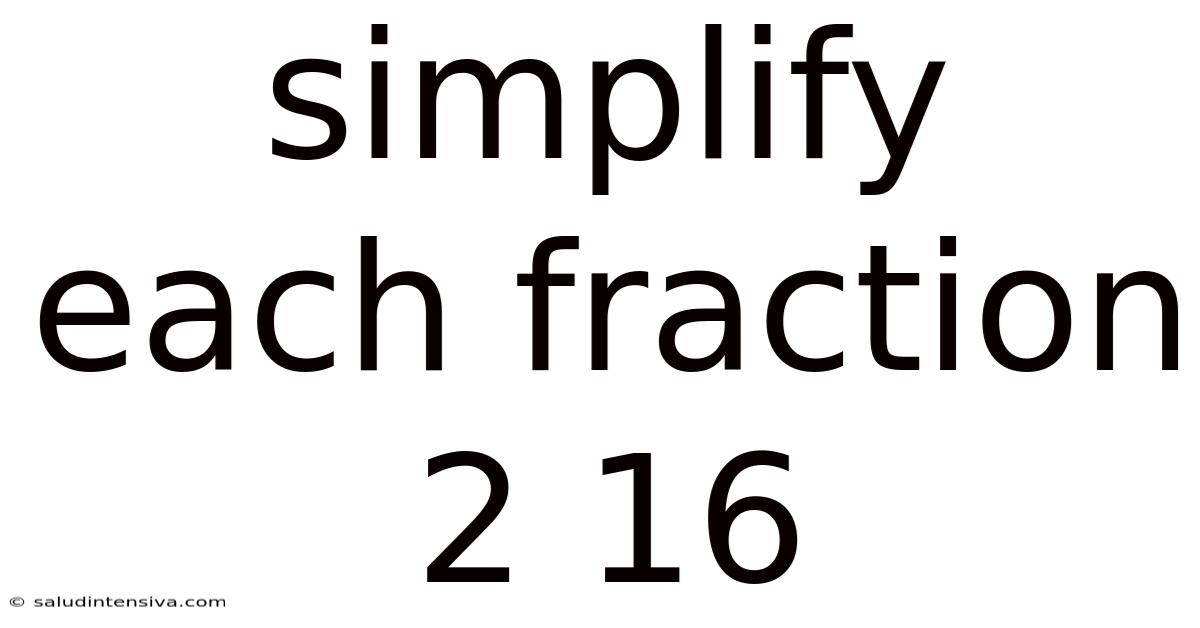
Table of Contents
Simplifying Fractions: A Deep Dive into 2/16 and Beyond
Understanding how to simplify fractions is a fundamental skill in mathematics, crucial for everything from basic arithmetic to advanced calculus. This comprehensive guide will not only show you how to simplify the fraction 2/16 but also provide a deep understanding of the underlying principles, equipping you with the skills to simplify any fraction with confidence. We'll cover the concept of greatest common divisors (GCD), explore different simplification methods, and address common misconceptions. By the end, you'll not only know the simplified form of 2/16 but also possess the tools to tackle more complex fraction simplification problems.
Understanding Fractions and Simplification
A fraction represents a part of a whole. It's written as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). For example, in the fraction 2/16, 2 is the numerator and 16 is the denominator. This means we have 2 parts out of a total of 16 parts.
Simplifying a fraction, also known as reducing a fraction, means expressing it in its simplest form. This is done by finding the greatest common divisor (GCD) of the numerator and denominator and dividing both by it. The GCD is the largest number that divides both the numerator and the denominator without leaving a remainder. A simplified fraction is one where the GCD of the numerator and denominator is 1; in other words, the numerator and denominator are relatively prime or coprime.
Finding the Greatest Common Divisor (GCD)
Finding the GCD is the key to simplifying fractions. There are several methods to find the GCD:
1. Listing Factors:
This method involves listing all the factors (numbers that divide evenly) of both the numerator and the denominator. Then, identify the largest factor that is common to both lists.
For example, let's find the GCD of 2 and 16:
- Factors of 2: 1, 2
- Factors of 16: 1, 2, 4, 8, 16
The largest common factor is 2. Therefore, the GCD of 2 and 16 is 2.
2. Prime Factorization:
This method involves breaking down both the numerator and the denominator into their prime factors (numbers divisible only by 1 and themselves). The GCD is then found by multiplying the common prime factors raised to the lowest power.
Let's find the GCD of 2 and 16 using prime factorization:
- Prime factorization of 2: 2
- Prime factorization of 16: 2 x 2 x 2 x 2 = 2⁴
The only common prime factor is 2, and the lowest power is 2¹. Therefore, the GCD is 2.
3. Euclidean Algorithm:
This is a more efficient method for larger numbers. It involves repeatedly applying the division algorithm until the remainder is 0. The last non-zero remainder is the GCD.
Let's find the GCD of 2 and 16 using the Euclidean algorithm:
- Divide 16 by 2: 16 = 2 x 8 + 0 The remainder is 0, so the GCD is the last non-zero remainder which is 2 (from the previous step if it existed).
Simplifying 2/16
Now that we know the GCD of 2 and 16 is 2, we can simplify the fraction 2/16:
Divide both the numerator and the denominator by the GCD (2):
2 ÷ 2 = 1 16 ÷ 2 = 8
Therefore, the simplified form of 2/16 is 1/8.
Simplifying Fractions: A Step-by-Step Guide
Let's generalize the process of simplifying fractions:
-
Find the GCD: Use any of the methods described above (listing factors, prime factorization, or the Euclidean algorithm) to determine the greatest common divisor of the numerator and the denominator.
-
Divide: Divide both the numerator and the denominator by the GCD.
-
Check: Verify that the resulting fraction is in its simplest form; the GCD of the new numerator and denominator should be 1.
Example: Simplify the fraction 12/18
-
Find the GCD:
- Factors of 12: 1, 2, 3, 4, 6, 12
- Factors of 18: 1, 2, 3, 6, 9, 18
- The GCD is 6.
-
Divide: 12 ÷ 6 = 2 18 ÷ 6 = 3
-
Check: The GCD of 2 and 3 is 1.
Therefore, the simplified form of 12/18 is 2/3.
More Complex Examples and Common Mistakes
Let's tackle some more challenging examples and address common errors:
Example 1: Simplify 48/72
-
Find the GCD: Using prime factorization: 48 = 2⁴ x 3 72 = 2³ x 3² The GCD is 2³ x 3 = 24
-
Divide: 48 ÷ 24 = 2 72 ÷ 24 = 3
The simplified fraction is 2/3.
Example 2: Simplify 105/135
-
Find the GCD: Using the Euclidean Algorithm: 135 = 105 x 1 + 30 105 = 30 x 3 + 15 30 = 15 x 2 + 0 The GCD is 15.
-
Divide: 105 ÷ 15 = 7 135 ÷ 15 = 9
The simplified fraction is 7/9.
Common Mistakes:
-
Not finding the greatest common divisor: Students sometimes find a common divisor but not the greatest common divisor, leading to an incomplete simplification. Always ensure you've found the largest common factor.
-
Incorrect division: Ensure that both the numerator and the denominator are divided by the GCD accurately.
-
Forgetting to check: Always verify that the simplified fraction is indeed in its simplest form.
Frequently Asked Questions (FAQ)
Q: What happens if the numerator is 0?
A: If the numerator is 0, the fraction simplifies to 0, regardless of the denominator (except for 0/0, which is undefined).
Q: What happens if the numerator and denominator are the same?
A: If the numerator and denominator are the same, the fraction simplifies to 1.
Q: Can I simplify a mixed number before converting it to an improper fraction?
A: Yes, you can simplify the fractional part of a mixed number before converting it to an improper fraction. This can often make the conversion and subsequent calculations easier.
Q: Are there any shortcuts for simplifying fractions?
A: While there isn't a single magic shortcut, recognizing simple common factors (like 2, 3, or 5) can speed up the process. Practice helps you develop an intuition for identifying common factors quickly.
Conclusion
Simplifying fractions is a crucial skill in mathematics. By mastering the techniques of finding the greatest common divisor and applying the steps outlined in this guide, you can confidently simplify any fraction, no matter the size of the numbers involved. Remember to practice regularly to build your proficiency and avoid common errors. With consistent effort, you'll transform from a novice to a fraction-simplifying expert! Understanding this fundamental concept will pave the way for more advanced mathematical concepts and problem-solving. Continue to explore and practice, and you'll find that the world of fractions becomes increasingly accessible and even enjoyable.
Latest Posts
Latest Posts
-
10 6 In Simplest Form
Sep 18, 2025
-
Lcm Of 9 And 18
Sep 18, 2025
-
Four To The Second Power
Sep 18, 2025
-
200kg Is How Many Pounds
Sep 18, 2025
-
How To Calculate Absolute Change
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about Simplify Each Fraction 2 16 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.