Solve D Rt For R
saludintensiva
Sep 16, 2025 · 6 min read
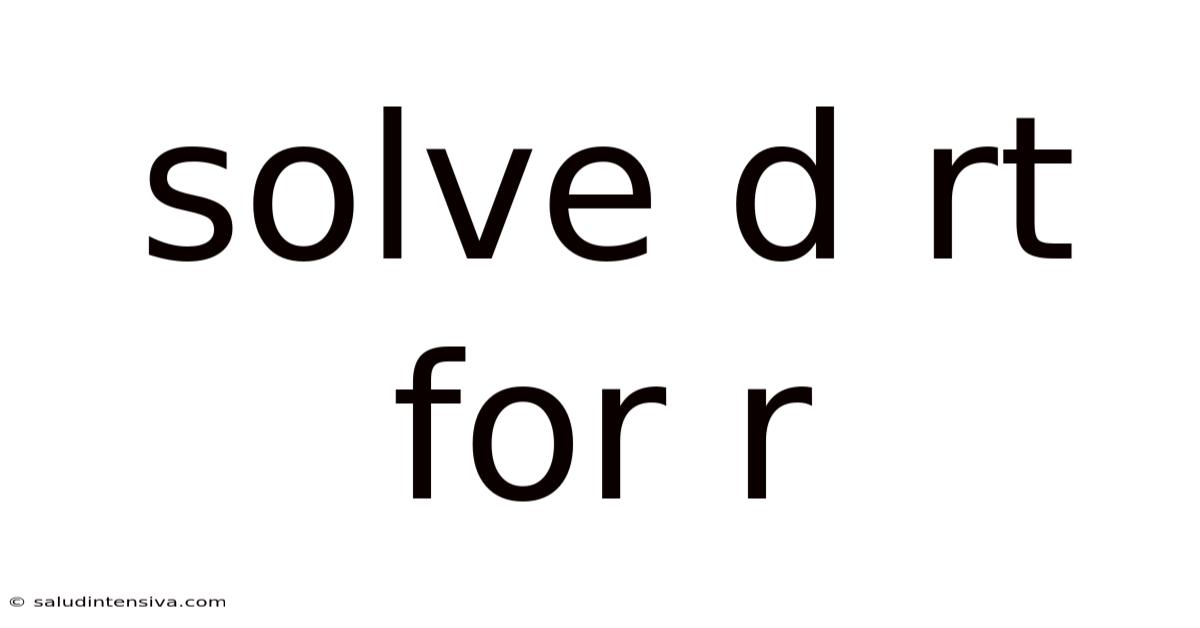
Table of Contents
Solving for 'r' in the Formula: d = rt
The formula d = rt is a fundamental concept in mathematics, particularly in areas like algebra and physics. It represents the relationship between distance (d), rate (r), and time (t). Understanding how to manipulate this formula, specifically solving for 'r', is crucial for solving various real-world problems involving speed, distance, and time. This comprehensive guide will walk you through the process, providing detailed explanations and examples to solidify your understanding. We'll explore the algebraic manipulation, delve into practical applications, and address frequently asked questions.
Understanding the Formula: d = rt
Before we dive into solving for 'r', let's ensure we understand the components of the formula d = rt:
-
d (distance): This represents the total distance covered. The units are typically miles, kilometers, meters, etc., depending on the context of the problem.
-
r (rate): This represents the rate of speed or velocity. The units are typically miles per hour (mph), kilometers per hour (kph), meters per second (m/s), etc. It's crucial to maintain consistent units throughout the problem.
-
t (time): This represents the duration of travel. The units are typically hours, minutes, or seconds, again, maintaining consistency is key.
The formula states that distance is equal to the rate multiplied by the time. For example, if you travel at a rate of 60 mph for 2 hours, the distance covered is 60 mph * 2 hours = 120 miles.
Solving for 'r': The Algebraic Manipulation
To solve for 'r' in the equation d = rt, we need to isolate 'r' on one side of the equation. This involves applying basic algebraic principles. Here's a step-by-step breakdown:
-
Start with the original equation:
d = rt -
Divide both sides by 't': To isolate 'r', we need to get rid of 't' on the right side. Since 'r' is multiplied by 't', we perform the inverse operation – division. Dividing both sides by 't' gives us:
d/t = rt/t -
Simplify: The 't' on the right side cancels out, leaving us with:
r = d/t
Therefore, the formula for rate (r) is: r = d/t. This means the rate is equal to the distance divided by the time.
Practical Applications: Real-World Examples
Let's illustrate the application of solving for 'r' with a few real-world examples:
Example 1: Calculating Average Speed
A car travels 240 miles in 4 hours. What is its average speed (rate)?
-
Known values:
- d (distance) = 240 miles
- t (time) = 4 hours
-
Applying the formula:
r = d/t = 240 miles / 4 hours = 60 mph
The car's average speed is 60 mph.
Example 2: Determining Travel Time Given Distance and Speed
A plane needs to cover a distance of 1500 kilometers. If it flies at an average speed of 750 kph, how long will the flight take? This example requires us to slightly modify our understanding. While we solve for 'r' initially, the problem actually asks us for 't'.
-
Known values:
- d (distance) = 1500 km
- r (rate) = 750 kph
-
Rearranging the formula: We already know that
r = d/t. To solve fort, we rearrange this formula to becomet = d/r -
Applying the formula:
t = d/r = 1500 km / 750 kph = 2 hours
The flight will take 2 hours.
Example 3: Calculating the Speed of a River Current
A boat travels 10 km downstream in 1 hour and 15 km upstream in 3 hours. Assume the speed of the boat in still water is constant. Find the speed of the river current. This is a more complex example requiring a system of equations.
Let's define:
b= speed of the boat in still waterc= speed of the river current
Downstream: The boat's speed is boosted by the current, so its effective speed is b + c.
Upstream: The boat's speed is slowed by the current, so its effective speed is b - c.
We can set up two equations:
- Equation 1 (downstream): 10 km = (b + c) * 1 hour
- Equation 2 (upstream): 15 km = (b - c) * 3 hours
Simplifying these equations gives us:
- Equation 1: 10 = b + c
- Equation 2: 5 = b - c
Now we can solve this system of equations. Adding the two equations eliminates 'c':
15 = 2b => b = 7.5 kph (boat speed in still water)
Substituting this value of 'b' back into Equation 1:
10 = 7.5 + c => c = 2.5 kph (speed of the river current)
The speed of the river current is 2.5 kph. This example demonstrates that solving for 'r' (or a related variable like boat speed) can be part of a larger problem-solving process.
Potential Pitfalls and Troubleshooting
While solving for 'r' is relatively straightforward, there are a few common pitfalls to be aware of:
-
Unit Consistency: Ensure all your units are consistent. If distance is in miles, time must be in hours to get a rate in mph. Inconsistency leads to incorrect answers.
-
Correct Order of Operations: Remember the order of operations (PEMDAS/BODMAS). Division should be performed after any necessary multiplications or additions within parentheses.
-
Significant Figures: In scientific contexts, pay attention to significant figures and round your final answer appropriately.
-
Word Problems: Carefully read and understand word problems. Identify the given information (distance, time, rate) and what the question is asking you to find.
Frequently Asked Questions (FAQ)
Q1: What if the time is given in minutes, but the rate needs to be in mph?
A1: Convert the time to hours before applying the formula. Remember there are 60 minutes in an hour. Divide the time in minutes by 60 to get the time in hours.
Q2: Can this formula be used for objects moving at varying speeds?
A2: Not directly. The formula d = rt assumes a constant rate. For objects with varying speeds, more advanced techniques like calculus (integration) are necessary to calculate the total distance. However, we can often use this formula to calculate average speed over the entire journey.
Q3: What if I have a problem where I need to solve for both 'r' and 't'?
A3: You'll need two independent equations relating distance, rate, and time. This often involves scenarios with two different legs of a journey or some other variation in the conditions. Systems of equations techniques (substitution, elimination) can be used to solve such problems.
Conclusion
Solving for 'r' in the equation d = rt is a fundamental skill in algebra and has wide-ranging applications in various fields. By understanding the algebraic manipulation, practicing with diverse examples, and being mindful of potential pitfalls, you can confidently solve problems involving distance, rate, and time. This skill is not only useful for academic purposes but also for tackling real-world scenarios involving travel, speed calculations, and other rate-related problems. Remember the core principle: rate is equal to distance divided by time. Mastering this formula empowers you to solve numerous problems efficiently and accurately.
Latest Posts
Latest Posts
-
Convert 53 F To C
Sep 16, 2025
-
How To Write A Sum
Sep 16, 2025
-
Whats 5625 As A Fraction
Sep 16, 2025
-
Wieviel Trinkgeld In Den Usa
Sep 16, 2025
-
Is 1 2 Greater Than 1
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about Solve D Rt For R . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.