Square Root Of Negative 25
saludintensiva
Sep 11, 2025 · 6 min read
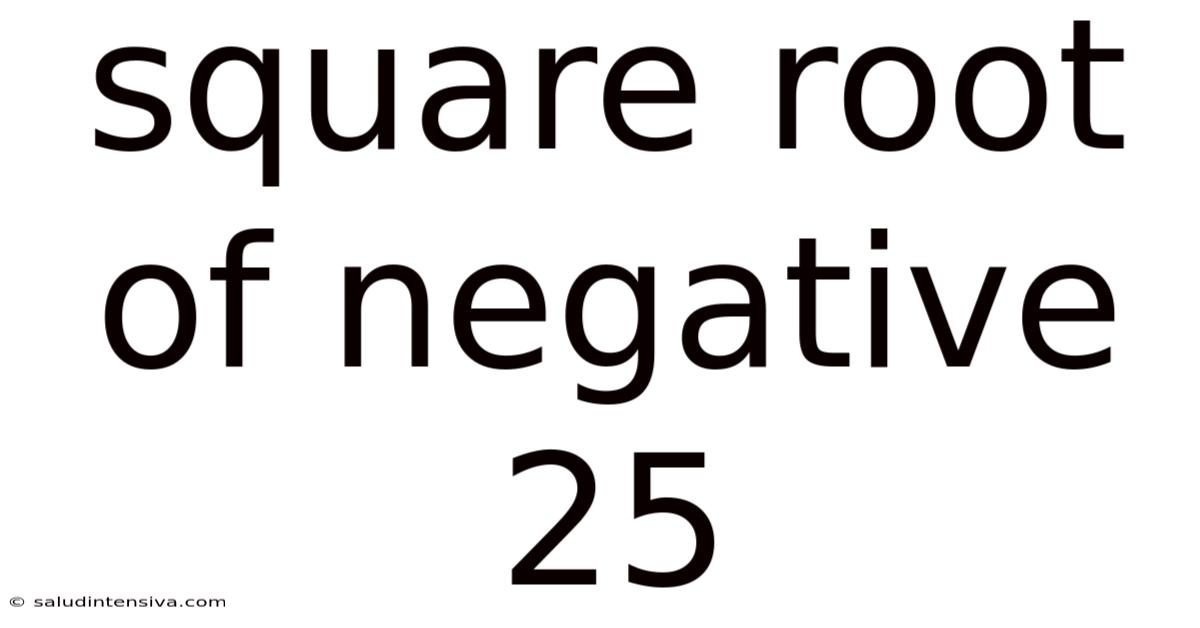
Table of Contents
Unveiling the Mystery: Understanding the Square Root of -25
The square root of -25, denoted as √-25, presents a fascinating challenge that takes us beyond the realm of real numbers into the intriguing world of complex numbers. This seemingly simple mathematical expression opens doors to a deeper understanding of number systems and their applications in various fields, from electrical engineering to quantum mechanics. This article will explore the concept of the square root of negative numbers, delve into the properties of imaginary and complex numbers, and provide a comprehensive explanation of √-25.
What is a Square Root?
Before we tackle the square root of -25, let's revisit the fundamental concept of a square root. The square root of a number 'x' is a value that, when multiplied by itself, results in 'x'. For example, the square root of 9 (√9) is 3, because 3 x 3 = 9. Similarly, the square root of 16 (√16) is 4. This seems straightforward with positive numbers. However, things get more interesting when we introduce negative numbers.
The Problem with Negative Square Roots in Real Numbers
In the realm of real numbers, we encounter a problem. There is no real number that, when multiplied by itself, yields a negative result. For instance, if we try to find the square root of -1 (√-1), we quickly realize that no real number satisfies this condition. 3 x 3 = 9, -3 x -3 = 9; neither produces -1. This limitation highlights the need for an extension of our number system.
Introducing the Imaginary Unit: i
To overcome the limitation of real numbers, mathematicians introduced the imaginary unit, denoted by the letter i. This imaginary unit is defined as the square root of -1:
i = √-1
This seemingly simple definition is revolutionary. It expands the number system beyond the familiar real numbers and opens up a whole new branch of mathematics. The imaginary unit allows us to express the square roots of negative numbers.
Understanding Imaginary Numbers
Imaginary numbers are numbers that can be expressed as a real number multiplied by the imaginary unit i. For example, 2i, 5i, and -3i are all imaginary numbers. These numbers represent points along the imaginary axis in the complex plane, a graphical representation we'll discuss later.
Calculating the Square Root of -25
Now, armed with the knowledge of the imaginary unit, let's calculate the square root of -25. We can rewrite √-25 as:
√-25 = √(25 x -1) = √25 x √-1
Since √25 = 5 and √-1 = i, the square root of -25 is:
√-25 = 5*i
Therefore, 5i is a solution. However, it's crucial to understand that, like many square root operations, there's another valid solution.
Multiple Solutions: The Importance of the ± Symbol
Remember that squaring a positive number and squaring a negative number both result in a positive number. Therefore, (-5i) x (-5i) also equals 25. Consequently, the complete solution for the square root of -25 is:
√-25 = ±5*i
The Complex Plane: Visualizing Complex Numbers
To better visualize and understand complex numbers, mathematicians use the complex plane. This plane has two axes: the real axis (horizontal) and the imaginary axis (vertical). Each complex number can be represented as a point on this plane. A complex number is expressed in the form:
a + b*i
where 'a' represents the real part and 'b' represents the imaginary part. For √-25, the real part is 0, and the imaginary part is ±5. This means the solutions lie on the imaginary axis, at points +5i and -5i.
Applications of Complex Numbers
While they might seem abstract, complex numbers have significant applications across various fields:
- Electrical Engineering: Complex numbers are used extensively in analyzing alternating current (AC) circuits. They simplify calculations involving impedance, phase shifts, and power.
- Quantum Mechanics: In quantum physics, complex numbers are essential for describing wave functions and the probabilistic nature of quantum phenomena.
- Signal Processing: Complex numbers are used in signal processing for representing and manipulating signals in the frequency domain.
- Fluid Dynamics: Certain fluid flow problems are solved using complex analysis, which relies on complex numbers.
- Fractals: Complex numbers are fundamental to generating many types of fractals, beautiful and complex geometric shapes.
Further Exploration: Powers of i and Complex Conjugates
The imaginary unit i exhibits intriguing properties when raised to different powers:
- i¹ = i
- i² = -1
- i³ = -i
- i⁴ = 1
- i⁵ = i (The pattern repeats)
Another important concept related to complex numbers is the complex conjugate. The complex conjugate of a complex number a + bi is a - bi. The product of a complex number and its conjugate is always a real number. This property is frequently used in simplifying expressions and solving equations involving complex numbers.
Frequently Asked Questions (FAQ)
-
Q: Are imaginary numbers "imaginary" in the sense that they don't exist? A: No, imaginary numbers are a mathematically valid extension of the real number system. They are just as "real" as real numbers, albeit existing in a different mathematical space. They are essential tools for solving problems in various scientific and engineering fields.
-
Q: Can I use a calculator to find the square root of -25? A: Most scientific calculators have the capability to handle complex numbers. You may need to switch to a "complex" or "imaginary" mode to perform the calculation correctly. The result should be displayed in the form a + b*i, where a is the real part and b is the imaginary part.
-
Q: What is the difference between a real number and a complex number? A: A real number only has a real component (e.g., 2, -5, 0.5, π). A complex number has both a real and an imaginary component (e.g., 2 + 3i, -1 - i, 4i). Real numbers can be considered a subset of complex numbers where the imaginary part is zero.
-
Q: Why are complex numbers important? A: Complex numbers provide a complete mathematical framework for solving many types of problems that cannot be solved using real numbers alone. Their applications are far-reaching and essential across various scientific and engineering disciplines.
Conclusion
The square root of -25, while seemingly simple, unveils a deeper understanding of mathematics. It necessitates the expansion from the familiar real number system to the broader world of complex numbers. Understanding the imaginary unit i and the concept of the complex plane allows us to solve equations that previously had no solution within the realm of real numbers. The applications of complex numbers extend far beyond theoretical mathematics; they are vital tools used in various scientific and engineering fields, demonstrating their practical importance and enriching our understanding of the world around us. Therefore, exploring the seemingly simple √-25 opens up a vast and fascinating area of mathematical exploration and application.
Latest Posts
Latest Posts
-
Square Root Of 13 Simplified
Sep 12, 2025
-
What Is 4 5 Equal To
Sep 12, 2025
-
84 Degrees F To C
Sep 12, 2025
-
What Is A 1 5 Ratio
Sep 12, 2025
-
Equivalent Fraction Of 8 20
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about Square Root Of Negative 25 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.