V Πr2h Solve For R
saludintensiva
Sep 21, 2025 · 6 min read
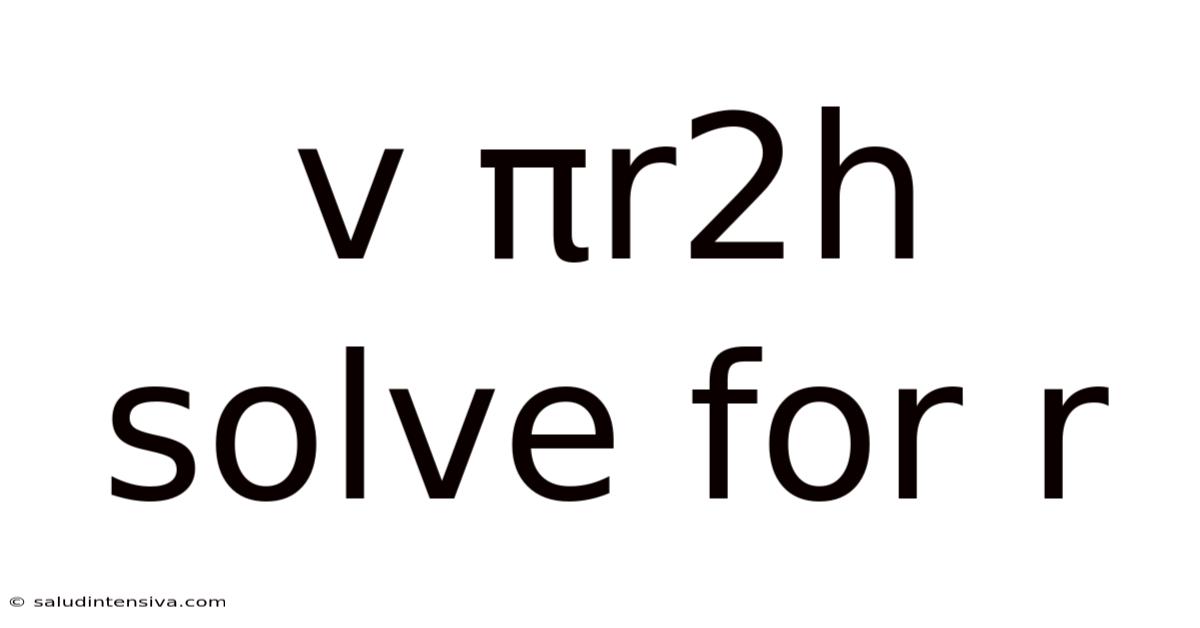
Table of Contents
Solving for the Radius (r) in the Cylinder Volume Formula: V = πr²h
Understanding the formula for the volume of a cylinder, V = πr²h, is fundamental in various fields, from geometry and engineering to architecture and even baking! This formula tells us the space occupied by a three-dimensional cylindrical shape. But what if you know the volume (V) and the height (h) of a cylinder, and you need to find the radius (r)? This article will guide you through solving for 'r' in the equation V = πr²h, step-by-step, offering explanations to enhance your understanding of the process and its applications. We will cover different approaches, delve into the underlying mathematical principles, and address frequently asked questions. Mastering this skill will significantly improve your problem-solving abilities in various mathematical contexts.
Understanding the Variables
Before diving into the solution, let's clarify what each variable in the formula represents:
-
V: Represents the volume of the cylinder. This is the total space enclosed within the cylinder's boundaries, usually measured in cubic units (e.g., cubic centimeters, cubic meters, cubic inches).
-
π (pi): Represents the mathematical constant pi, approximately equal to 3.14159. Pi is the ratio of a circle's circumference to its diameter and is crucial in all circular calculations.
-
r: Represents the radius of the cylinder's circular base. This is the distance from the center of the circular base to any point on its circumference.
-
h: Represents the height of the cylinder. This is the perpendicular distance between the two circular bases.
Step-by-Step Solution for r
To solve for 'r', we need to isolate 'r' on one side of the equation V = πr²h. Here's a detailed breakdown of the steps involved:
-
Divide both sides by πh: The first step is to remove π and h from the right-hand side of the equation. Since π and h are multiplied by r², we can achieve this by dividing both sides of the equation by πh. This gives us:
V / (πh) = r²
-
Take the square root of both sides: Now we have r² isolated, but we need to find the value of r, not r². To do this, we take the square root of both sides of the equation. Remember, the square root of a number is a value that, when multiplied by itself, gives the original number. Therefore:
√[V / (πh)] = r
Therefore, the formula to solve for the radius (r) is:
r = √[V / (πh)]
Illustrative Examples
Let's solidify our understanding with some examples:
Example 1:
A cylindrical water tank has a volume of 150 cubic meters and a height of 5 meters. What is the radius of the tank?
-
Substitute the known values: We have V = 150 m³, and h = 5 m. Substitute these values into our derived formula:
r = √[150 m³ / (π * 5 m)]
-
Calculate: Using a calculator, we approximate π as 3.14159:
r ≈ √[150 / (3.14159 * 5)] ≈ √[9.549] ≈ 3.09 meters
Therefore, the radius of the water tank is approximately 3.09 meters.
Example 2:
A cylindrical candle has a volume of 200 cubic centimeters and a radius of 4 centimeters. What is the height of the candle? (Note: This example slightly reverses the problem, allowing us to demonstrate the application of the rearranged formula and check our understanding).
First, let's rearrange the original formula V = πr²h to solve for h:
h = V / (πr²)
Now, let's substitute our known values (V = 200 cm³, r = 4 cm):
h = 200 cm³ / (π * (4 cm)²)
h ≈ 200 / (3.14159 * 16) ≈ 3.98 cm
The height of the candle is approximately 3.98 centimeters.
Mathematical Explanation and Underlying Principles
The derivation of the formula for the volume of a cylinder (V = πr²h) stems from the understanding of the area of a circle and the concept of volume as a three-dimensional extension of area.
-
Area of a Circle: The area of a circle is given by the formula A = πr². This represents the base area of our cylinder.
-
Volume as Area times Height: Imagine the cylinder as a stack of infinitely thin circular disks. The volume of each disk is its area multiplied by its infinitesimal thickness. Summing up the volumes of all these disks gives us the total volume of the cylinder, which is the base area (πr²) multiplied by the height (h). This leads to the formula V = πr²h.
Solving for 'r' involves reversing this process – isolating the radius term through algebraic manipulation, revealing its relationship with the volume and height. The square root operation is essential because the radius is squared in the original volume formula.
Practical Applications
Understanding how to solve for the radius of a cylinder has wide-ranging practical applications:
-
Engineering: Calculating the dimensions of pipes, tanks, and other cylindrical components in various engineering projects.
-
Manufacturing: Determining the dimensions of cylindrical containers, packaging, and components.
-
Architecture: Designing cylindrical structures, calculating material requirements, and ensuring structural integrity.
-
Science: Analyzing cylindrical samples in experiments, calculating volumes in physics and chemistry.
-
Everyday Life: Estimating the volume of everyday cylindrical objects like cans, bottles, and even tree trunks.
Frequently Asked Questions (FAQ)
Q1: What if I get a negative value when solving for 'r'?
A1: A negative radius is physically impossible. If you obtain a negative value, it likely indicates an error in your calculations or in the input values (V and h). Double-check your calculations and ensure that the volume and height are positive values.
Q2: Can I use this formula for cylinders that are not perfectly straight?
A2: No, this formula is specifically for right circular cylinders – cylinders with straight sides and circular bases. For cylinders with curved sides or non-circular bases, you would need more complex formulas or methods to calculate the volume and radius.
Q3: How do I handle units in my calculations?
A3: Maintain consistent units throughout your calculations. If the volume is given in cubic meters and the height in meters, the radius will be in meters. If you mix units (e.g., cubic centimeters and meters), you'll get an incorrect result. Always ensure unit consistency.
Q4: What if I only know the volume and radius? How do I find the height?
A4: Rearrange the formula V = πr²h to solve for h: h = V / (πr²).
Q5: Are there any online calculators to help with this calculation?
A5: While numerous online calculators exist for various mathematical functions, understanding the underlying process is crucial. Using a calculator is helpful for efficient computation but shouldn’t replace the understanding of how the formula is derived and applied.
Conclusion
Solving for the radius (r) in the cylinder volume formula, V = πr²h, involves a straightforward yet important application of algebraic manipulation and mathematical principles. By mastering this skill, you'll enhance your problem-solving capabilities and gain a deeper understanding of geometrical concepts. Remember the derived formula: r = √[V / (πh)]. Always pay attention to units and ensure your input values are correct to avoid errors. This knowledge will prove invaluable across a multitude of applications, from academic pursuits to real-world problem-solving. Practicing with various examples will reinforce your understanding and build your confidence in tackling similar mathematical challenges.
Latest Posts
Latest Posts
-
What Is The Range Number
Sep 21, 2025
-
What Is 10 Of 145000
Sep 21, 2025
-
Convert Cu Yards To Tons
Sep 21, 2025
-
87 Degrees Fahrenheit To Celsius
Sep 21, 2025
-
Solve For X 2 8
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about V Πr2h Solve For R . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.