What Is 1/2 + 2/6
saludintensiva
Sep 18, 2025 · 6 min read
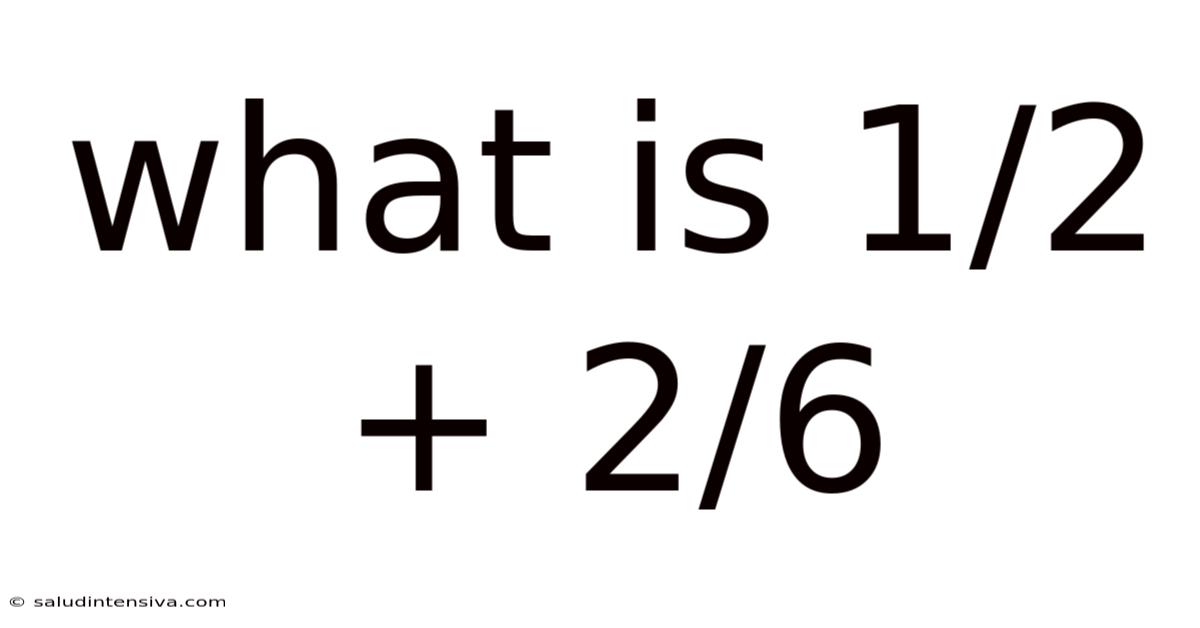
Table of Contents
Decoding Fractions: A Deep Dive into 1/2 + 2/6
Understanding fractions is a fundamental building block in mathematics. This seemingly simple equation, 1/2 + 2/6, provides an excellent opportunity to explore various concepts, from basic addition to crucial skills in simplifying fractions and finding common denominators. This article will guide you through a step-by-step solution, explaining the underlying principles and offering valuable insights for anyone looking to strengthen their fractional arithmetic skills. We'll move beyond just finding the answer and delve into the why behind the methods, ensuring a comprehensive understanding.
Introduction to Fractions: Understanding the Basics
Before we tackle the addition problem, let's refresh our understanding of what fractions represent. A fraction is a part of a whole. It's expressed as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). The denominator tells us how many equal parts the whole is divided into, while the numerator tells us how many of those parts we're considering. For example, in the fraction 1/2, the denominator (2) indicates the whole is divided into two equal parts, and the numerator (1) signifies we're dealing with one of those parts – one-half.
Step-by-Step Solution: 1/2 + 2/6
The addition of fractions requires a common denominator. This means that both fractions must have the same denominator before we can add their numerators. Let's break down the process:
1. Finding the Least Common Denominator (LCD):
The denominators in our equation are 2 and 6. To find the LCD, we identify the least common multiple (LCM) of these two numbers. The multiples of 2 are 2, 4, 6, 8, 10... The multiples of 6 are 6, 12, 18, 24... The smallest number that appears in both lists is 6. Therefore, the LCD is 6.
2. Converting Fractions to the LCD:
Now, we need to convert both fractions so they have a denominator of 6.
-
1/2: To change the denominator from 2 to 6, we multiply both the numerator and the denominator by 3 (because 2 x 3 = 6). This gives us (1 x 3) / (2 x 3) = 3/6. This doesn't change the value of the fraction; it simply represents it in a different form.
-
2/6: This fraction already has a denominator of 6, so we don't need to change it.
3. Adding the Fractions:
Now that both fractions have the same denominator (6), we can add their numerators:
3/6 + 2/6 = (3 + 2) / 6 = 5/6
Therefore, 1/2 + 2/6 = 5/6
Simplifying Fractions: A Crucial Step
While 5/6 is the correct answer, it's always good practice to check if a fraction can be simplified. A fraction is simplified when its numerator and denominator have no common factors other than 1. In this case, 5 and 6 have no common factors besides 1, so 5/6 is already in its simplest form.
Visualizing Fractions: A Geometric Approach
Understanding fractions becomes more intuitive when visualized. Imagine a circle divided into six equal slices. The fraction 1/2 represents three of these slices (half the circle), and 2/6 represents two of these slices. Adding these together gives you a total of five slices, which is 5/6 of the circle. This visual representation helps solidify the concept of adding fractions.
The Importance of Common Denominators: A Deeper Look
The requirement of a common denominator before adding fractions stems from the fundamental principle that we can only add or subtract quantities that represent the same units. Think of it like adding apples and oranges. You can't directly add them without first converting them to a common unit (e.g., pieces of fruit). Similarly, fractions with different denominators represent parts of different wholes. A common denominator ensures we're adding parts of the same whole.
Alternative Methods: Finding the LCD
While we found the LCD by listing multiples, there are other methods, particularly useful for larger numbers:
-
Prime Factorization: This method involves breaking down each denominator into its prime factors. The LCD is then found by taking the highest power of each prime factor present in the denominators. For example:
2 = 2 6 = 2 x 3
The LCD is 2 x 3 = 6.
-
Greatest Common Divisor (GCD): You can also use the GCD to simplify the process. The relationship between the LCM and GCD is: LCM(a,b) * GCD(a,b) = a*b. Find the GCD of 2 and 6 (which is 2), then use this formula to calculate the LCM (which is 6).
Expanding the Concept: Adding More Than Two Fractions
The principles discussed above apply to adding more than two fractions. We still need to find the LCD of all the denominators and convert each fraction to that common denominator before adding the numerators.
Applications of Fraction Addition in Real Life
Adding fractions isn't just a theoretical exercise; it's a practical skill used in numerous real-world situations:
-
Cooking and Baking: Recipes often involve fractional measurements. Adding ingredients requires understanding fraction addition.
-
Construction and Engineering: Precise measurements are crucial in these fields, and working with fractions is essential for accurate calculations.
-
Finance: Dealing with percentages and proportions involves fraction manipulation.
Frequently Asked Questions (FAQ)
Q: What if the fractions have different signs (positive and negative)?
A: The process is similar, but remember the rules of adding and subtracting signed numbers. For example: 1/2 + (-2/6) would involve finding the common denominator (6), converting the fractions (3/6 + (-2/6)), and then adding the numerators, remembering that adding a negative number is the same as subtraction. This would result in 1/6.
Q: What happens if the resulting fraction can be simplified?
A: Always simplify the final fraction to its lowest terms by dividing both the numerator and the denominator by their greatest common divisor (GCD). This makes the fraction easier to understand and use.
Q: Can I use a calculator to add fractions?
A: While calculators can add fractions directly, it's beneficial to understand the underlying principles. Calculators should be used as a tool to verify your work, not replace the learning process.
Conclusion: Mastering Fraction Addition
Understanding fraction addition is crucial for building a strong foundation in mathematics. By mastering the concepts of common denominators, simplifying fractions, and visualizing fractional quantities, you can confidently tackle more complex mathematical problems. The seemingly simple equation, 1/2 + 2/6 = 5/6, serves as a gateway to a deeper understanding of fractional arithmetic and its wide-ranging applications. Remember, consistent practice and a focus on understanding the underlying principles are key to success. Don't hesitate to revisit these steps and practice with different fraction combinations to reinforce your learning. The more you work with fractions, the more intuitive and comfortable you'll become.
Latest Posts
Latest Posts
-
24 Degrees F To C
Sep 18, 2025
-
How To Measure Running Distance
Sep 18, 2025
-
Lb Ft2 To Kg M2
Sep 18, 2025
-
What Is Equal To 9 12
Sep 18, 2025
-
47 50 As A Decimal
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about What Is 1/2 + 2/6 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.