What Is 1/3 In Percentage
saludintensiva
Sep 18, 2025 · 5 min read
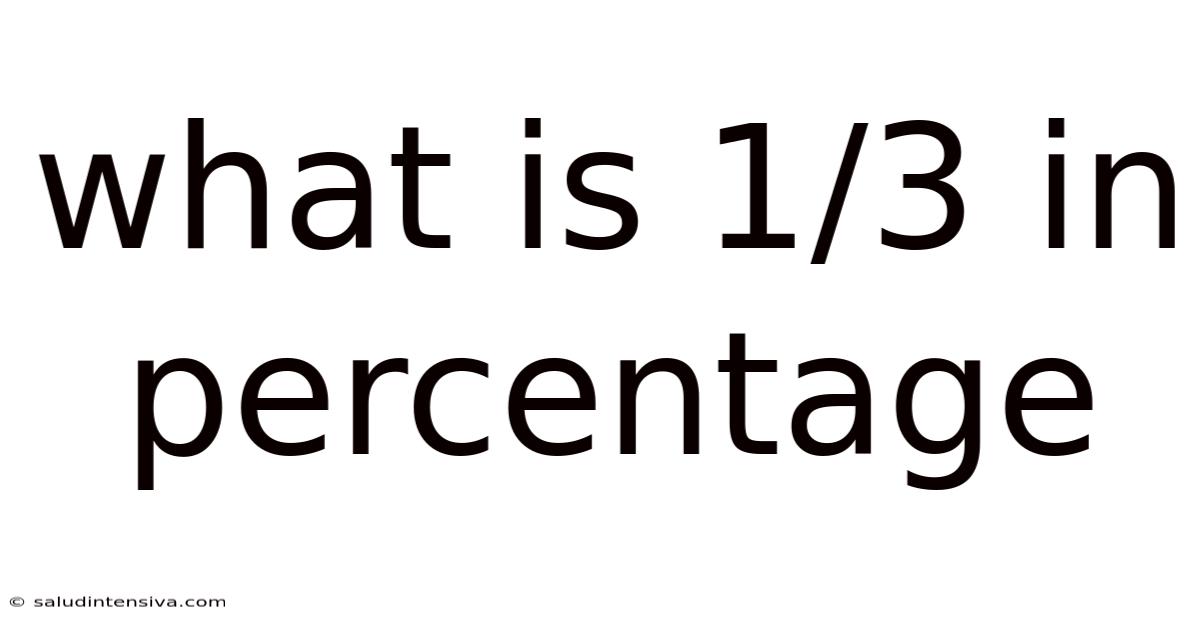
Table of Contents
What is 1/3 in Percentage? A Comprehensive Guide
Understanding fractions and their percentage equivalents is a fundamental skill in mathematics with applications across various fields, from finance and cooking to engineering and data analysis. This article will delve into the conversion of the fraction 1/3 into a percentage, explaining the process in detail, addressing common misconceptions, and providing practical examples. We'll explore the underlying mathematical concepts and discuss why the result isn't a neat, whole number percentage. By the end, you'll not only know the answer but also understand the 'why' behind it, enhancing your mathematical proficiency.
Understanding Fractions and Percentages
Before we dive into converting 1/3 into a percentage, let's refresh our understanding of these fundamental mathematical concepts.
A fraction represents a part of a whole. It consists of two numbers: the numerator (the top number) and the denominator (the bottom number). The numerator indicates how many parts we have, while the denominator indicates how many equal parts the whole is divided into. For example, in the fraction 1/3, the numerator is 1 and the denominator is 3, meaning we have one part out of a total of three equal parts.
A percentage, on the other hand, is a way of expressing a number as a fraction of 100. The word "percent" literally means "out of one hundred" ( per centum in Latin). Percentages are often used to represent proportions or ratios, making them easy to compare and understand. For instance, 50% means 50 out of 100, or 50/100, which simplifies to 1/2.
Converting Fractions to Percentages: The Method
Converting a fraction to a percentage involves two main steps:
- Convert the fraction to a decimal: To do this, divide the numerator by the denominator.
- Convert the decimal to a percentage: Multiply the decimal by 100 and add the "%" symbol.
Let's apply these steps to our fraction, 1/3:
-
Convert 1/3 to a decimal: 1 ÷ 3 = 0.33333... Notice that this is a repeating decimal; the digit 3 continues infinitely. We often round this to a certain number of decimal places for practical purposes.
-
Convert the decimal to a percentage: 0.3333... × 100 = 33.333...% Again, we have a repeating decimal in the percentage representation.
Therefore, 1/3 is approximately 33.33%. The ellipsis (...) indicates that the decimal continues infinitely. The accuracy of the percentage depends on the number of decimal places we choose to use.
Why is it a Repeating Decimal?
The reason 1/3 results in a repeating decimal is because 3 is not a factor of 10 (or any power of 10, such as 100, 1000, etc.). When we perform the division, we are essentially trying to express one part out of three equal parts using a base-10 number system. This doesn't divide evenly, resulting in a repeating pattern. This isn't a flaw in the system; it's simply a consequence of the relationship between the number 3 and the base-10 number system.
Different Levels of Precision
As mentioned earlier, the percentage equivalent of 1/3 is an infinitely repeating decimal. The level of precision needed depends on the context.
-
For everyday calculations: Rounding to 33.33% is usually sufficient. This provides a good approximation for most practical purposes.
-
For scientific or engineering applications: A higher degree of precision might be necessary. You might use more decimal places, or even represent the answer as a fraction (1/3) to maintain complete accuracy. Scientific calculators often display repeating decimals accurately, avoiding the need for rounding.
-
For financial calculations: Accuracy is paramount. While rounding is often done for display, the underlying calculations should ideally use the full, unrounded decimal value to minimize accumulated errors.
Practical Applications and Examples
The concept of 1/3 as a percentage finds application in numerous real-world situations:
-
Discount Calculations: A store offers a 1/3 discount on an item. To calculate the discount amount, you would multiply the item's price by 33.33% (approximately).
-
Recipe Conversions: If a recipe calls for 1/3 cup of sugar, you can convert that to a percentage of a cup (approximately 33.33%).
-
Data Analysis: When dealing with proportions or ratios, expressing them as percentages can improve clarity and facilitate comparisons. For instance, if 1/3 of a survey respondents answered 'yes,' you'd report this as approximately 33.33%.
Understanding the Limitations of Rounding
It's crucial to remember that rounding introduces a small degree of error. While 33.33% is a close approximation of 1/3, it is not precisely equal. The difference is insignificant in many contexts, but in situations requiring high accuracy (like precise scientific measurements or complex financial models), using the fraction 1/3 directly, or retaining more decimal places, is preferable to prevent compounding errors.
Frequently Asked Questions (FAQ)
Q: Is 1/3 exactly equal to 33.33%?
A: No, 1/3 is approximately equal to 33.33%. The decimal representation of 1/3 is 0.3333... (a repeating decimal), and thus the percentage equivalent is also a repeating decimal (33.333...). 33.33% is a rounded approximation.
Q: How can I express 1/3 as a percentage without rounding?
A: You can express it as 33.333...% The ellipsis indicates the repeating decimal. Alternatively, you can leave it as the fraction 1/3, as this maintains complete accuracy.
Q: What other fractions produce repeating decimals?
A: Many fractions with denominators that are not factors of powers of 10 will result in repeating decimals. Examples include 1/7, 1/9, 2/3, and 5/6.
Q: If I need to perform multiple calculations using 1/3, should I use the rounded percentage or the fraction?
A: For multiple calculations, it's generally better to use the fraction (1/3) to minimize the accumulation of rounding errors. Only round the final result if necessary.
Conclusion
Understanding the conversion of fractions to percentages is essential for various mathematical applications. While 1/3 converts to approximately 33.33%, it's important to recognize that this is an approximation due to the repeating decimal nature of the result. The choice between using the rounded percentage or the fraction depends on the level of accuracy required. Remembering the underlying mathematical principles and the limitations of rounding will ensure greater accuracy and understanding in your calculations. Always consider the context of your problem to determine the appropriate level of precision.
Latest Posts
Latest Posts
-
How To Factorise Cubic Equations
Sep 19, 2025
-
Cube Root Of X 2
Sep 19, 2025
-
Write 2 10 In Lowest Terms
Sep 19, 2025
-
Whats 1500 In Military Time
Sep 19, 2025
-
Is 15 Prime Or Composite
Sep 19, 2025
Related Post
Thank you for visiting our website which covers about What Is 1/3 In Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.