What Is 1/5 Of 10
saludintensiva
Sep 20, 2025 · 5 min read
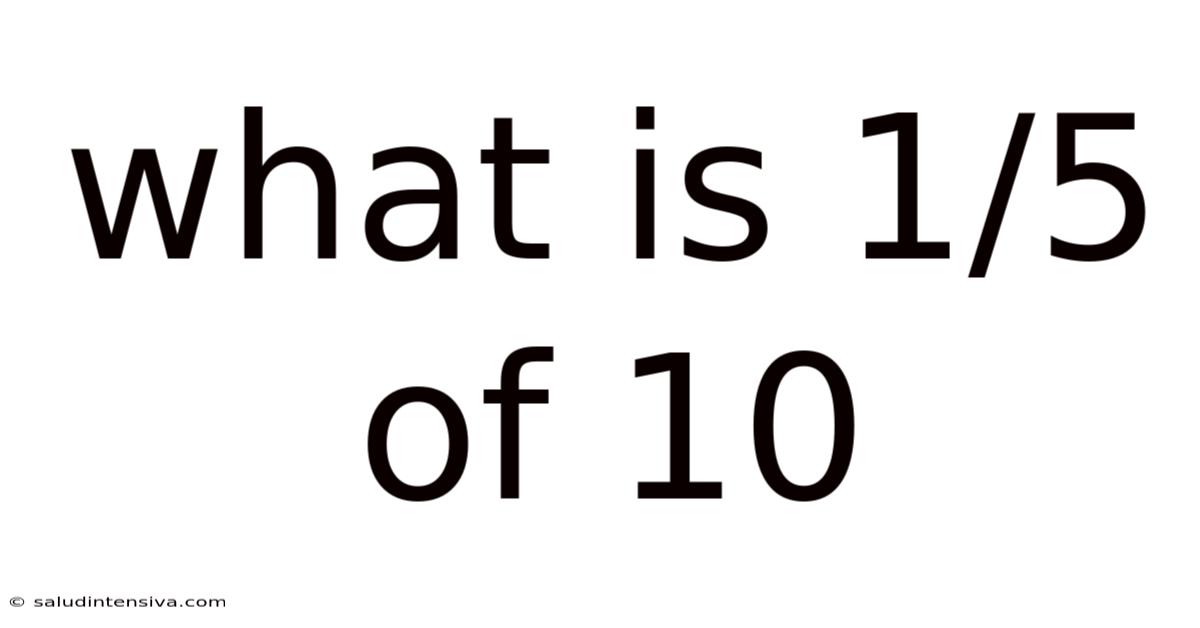
Table of Contents
What is 1/5 of 10? A Deep Dive into Fractions and Their Applications
Finding 1/5 of 10 might seem like a simple calculation, a problem easily solved by a child. However, this seemingly straightforward question opens the door to a much broader understanding of fractions, their applications in everyday life, and the underlying mathematical principles that govern them. This article will not only answer the question directly but also explore the concept of fractions, various methods for solving fractional problems, and the practical significance of this seemingly simple calculation.
Understanding Fractions: The Building Blocks of Mathematics
A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). The denominator indicates how many equal parts the whole is divided into, while the numerator indicates how many of those parts are being considered. In the fraction 1/5, the denominator, 5, means the whole is divided into five equal parts, and the numerator, 1, means we are considering only one of those parts.
Fractions are essential in various fields, from cooking and baking (measuring ingredients) to construction (measuring materials) and finance (calculating percentages and proportions). Understanding fractions is crucial for basic arithmetic, algebra, and more advanced mathematical concepts.
Calculating 1/5 of 10: Three Approaches
There are several ways to calculate 1/5 of 10, each offering a slightly different perspective on the underlying mathematical principles:
1. Direct Multiplication:
The most straightforward method is to multiply the fraction by the whole number. Remember that "of" in mathematics often translates to multiplication. Therefore, finding 1/5 of 10 is the same as calculating (1/5) * 10.
To perform this calculation:
- Multiply the numerator by the whole number: 1 * 10 = 10
- Keep the denominator the same: The denominator remains 5.
- Simplify the resulting fraction: This gives us 10/5.
- Convert the improper fraction to a whole number: 10 divided by 5 equals 2.
Therefore, 1/5 of 10 is 2.
2. Division:
Alternatively, we can interpret the problem as dividing the whole number (10) by the denominator (5) and then multiplying the result by the numerator (1).
- Divide the whole number by the denominator: 10 / 5 = 2
- Multiply the result by the numerator: 2 * 1 = 2
This method also yields the answer: 2. This approach highlights the inverse relationship between multiplication and division within fractions.
3. Visual Representation:
A visual representation can be particularly helpful for grasping the concept. Imagine a pizza cut into 5 equal slices. 1/5 of the pizza represents one slice. If you have 10 pizzas, each cut into 5 slices, you would have a total of 50 slices (10 pizzas * 5 slices/pizza). 1/5 of those 50 slices is 10 slices (50 slices / 5), which is equivalent to 2 whole pizzas (10 slices / 5 slices/pizza). This visualization reinforces the answer: 2.
Expanding the Concept: Working with Different Fractions and Whole Numbers
Let's expand our understanding by exploring how to calculate other fractions of different whole numbers. The same principles apply:
- Finding 2/5 of 10: This involves multiplying (2/5) * 10. Following the multiplication method, we get (2 * 10) / 5 = 20/5 = 4.
- Finding 1/3 of 15: This involves multiplying (1/3) * 15. This yields (1 * 15) / 3 = 15/3 = 5.
- Finding 3/4 of 20: This is (3/4) * 20 = (3 * 20) / 4 = 60/4 = 15.
These examples illustrate the versatility of the methods discussed earlier. Regardless of the specific fraction and whole number involved, the core principle—multiplying the fraction by the whole number—remains consistent.
Practical Applications: Fractions in Real Life
The seemingly simple calculation of 1/5 of 10 has far-reaching implications in various real-world scenarios. Here are a few examples:
- Sharing resources: Imagine sharing 10 candies among 5 friends. Each friend gets 1/5 of the candies, which is 2 candies.
- Cooking and baking: A recipe might call for 1/5 of a cup of sugar in a larger recipe. Understanding fractions is crucial for accurately measuring ingredients.
- Calculating discounts: A store offers a 20% discount (which is 1/5) on an item costing $10. The discount amount is 1/5 of $10, or $2.
- Financial calculations: Fractions are fundamental for calculating interest rates, proportions, and various other financial metrics.
Frequently Asked Questions (FAQ)
Q: What if the fraction is a mixed number (e.g., 1 1/5)?
A: Convert the mixed number to an improper fraction first. 1 1/5 is equal to (1 * 5 + 1)/5 = 6/5. Then, proceed with the multiplication as described earlier.
Q: Can I use a calculator for these calculations?
A: Absolutely! Calculators can simplify the process, especially when dealing with more complex fractions and numbers. However, understanding the underlying principles is still crucial for problem-solving and building mathematical intuition.
Q: What if the result is not a whole number?
A: You will often obtain a fraction or a decimal as a result. For example, 1/3 of 10 is 10/3 which is approximately 3.333... This is perfectly acceptable, and sometimes more accurate than rounding to a whole number.
Q: How do I handle larger numbers or more complex fractions?
A: The same principles apply. Multiply the numerator by the whole number, keep the denominator, and simplify the resulting fraction. For very large or complex fractions, a calculator can be helpful.
Conclusion: Beyond the Simple Calculation
The seemingly simple question, "What is 1/5 of 10?" serves as a gateway to a more profound understanding of fractions and their importance in various aspects of life. Mastering this concept forms a bedrock for more advanced mathematical studies and practical applications in various fields. The methods explored here – direct multiplication, division, and visual representation – offer diverse approaches to tackling such problems, catering to different learning styles and enhancing overall comprehension. Beyond the answer of 2, the true value lies in the enhanced comprehension of fundamental mathematical principles and their real-world applications. Remember that the core concepts remain consistent even as the numbers and complexity of the problems increase. So keep practicing, keep exploring, and keep expanding your mathematical horizons.
Latest Posts
Latest Posts
-
How Long Is 136 Minutes
Sep 20, 2025
-
A Cubed B Cubed
Sep 20, 2025
-
270 Degrees Celsius In Fahrenheit
Sep 20, 2025
-
21 Cm How Many Inches
Sep 20, 2025
-
9600 Sq Ft To Acres
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about What Is 1/5 Of 10 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.