What Is 1/6 Of 120
saludintensiva
Sep 23, 2025 · 5 min read
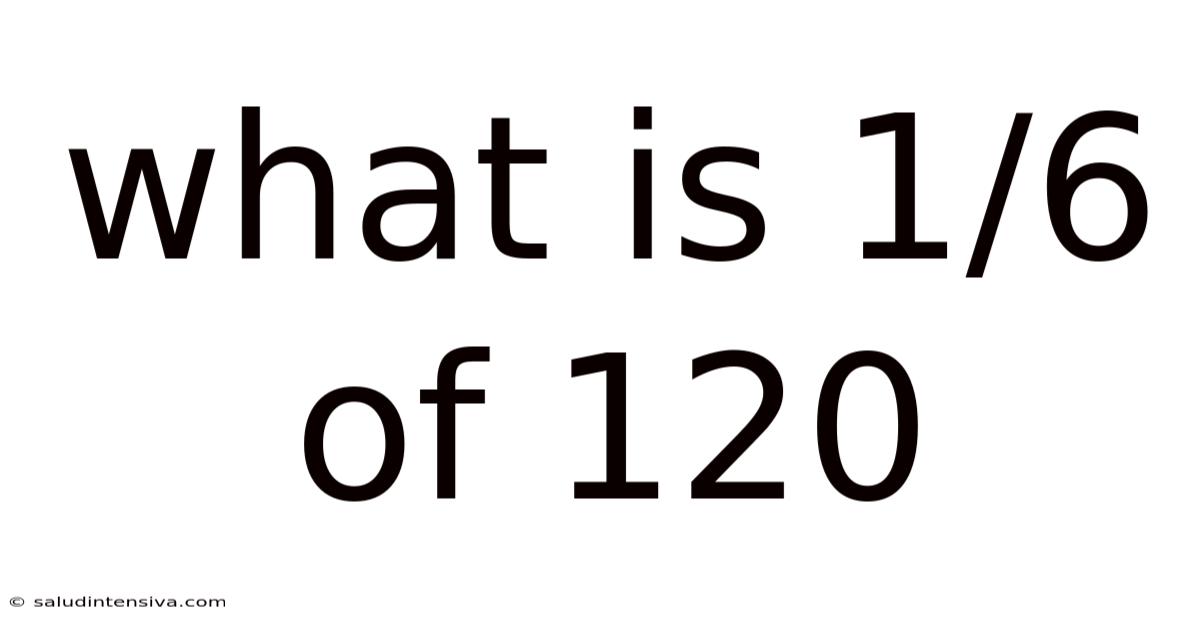
Table of Contents
What is 1/6 of 120? A Deep Dive into Fractions and Their Applications
Finding 1/6 of 120 might seem like a simple arithmetic problem, suitable only for elementary school students. However, understanding how to solve this seemingly basic equation unlocks a deeper understanding of fractions, their practical applications, and their importance in various fields, from cooking and construction to advanced mathematics and finance. This article will not only provide the answer but also explore the underlying concepts, offering various methods of calculation and showcasing the broader significance of fractional arithmetic.
Understanding Fractions: The Building Blocks of Calculation
Before diving into the solution, let's refresh our understanding of fractions. A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). The numerator indicates how many parts you have, while the denominator shows how many equal parts the whole is divided into. In the problem "What is 1/6 of 120?", 1/6 is the fraction, where 1 is the numerator and 6 is the denominator. This means we're looking for one part out of six equal parts of the whole (120).
Method 1: Division – The Direct Approach
The most straightforward way to find 1/6 of 120 is through division. Since "of" in mathematics signifies multiplication, the problem can be rewritten as (1/6) * 120. To solve this:
- Convert the fraction to a decimal: 1/6 is approximately 0.1667.
- Multiply the decimal by 120: 0.1667 * 120 ≈ 20
Therefore, 1/6 of 120 is approximately 20. Note that the use of a decimal approximation can lead to slight inaccuracies. Let's explore a more precise method.
Method 2: Division by the Denominator – The Precise Method
A more accurate approach avoids decimal approximations. We can directly divide 120 by the denominator (6):
- Divide: 120 ÷ 6 = 20
This method gives us the exact answer: 1/6 of 120 is 20. This highlights the direct relationship between fractions and division; finding a fraction of a number is essentially dividing that number by the denominator of the fraction.
Method 3: Simplifying Before Calculation – An Advanced Approach
While not strictly necessary in this simple example, understanding how to simplify fractions before calculation is crucial for more complex problems. If the numerator and denominator shared a common factor, we could simplify the fraction before multiplying. In this case, there's no common factor between 1 and 6. However, let's consider an example: finding 2/6 of 120.
- Simplify the fraction: 2/6 can be simplified to 1/3 by dividing both the numerator and the denominator by 2.
- Calculate: (1/3) * 120 = 120 ÷ 3 = 40
Therefore, 2/6 of 120 is 40. This illustrates how simplifying fractions can make calculations easier and more efficient.
Practical Applications: Where Fractions Matter
The ability to calculate fractions is essential in numerous everyday situations. Here are a few examples:
- Cooking and Baking: Recipes often require fractional measurements of ingredients. Understanding fractions is crucial for accurately measuring ingredients and ensuring the desired outcome. For instance, a recipe might call for 1/4 cup of sugar or 2/3 of a teaspoon of salt.
- Construction and Engineering: Precise measurements and calculations are critical in construction and engineering. Fractions are used extensively in blueprints, design specifications, and material calculations. For example, determining the length of a beam might require understanding fractions of feet or inches.
- Finance and Budgeting: Fractions are used to represent portions of a whole in financial calculations. Understanding percentages (which are essentially fractions with a denominator of 100) is vital for managing budgets, calculating interest rates, and understanding investments. For instance, calculating sales tax or discounts often involves fractions.
- Data Analysis and Statistics: Fractions and proportions are foundational in data analysis and statistics. Understanding fractions helps in interpreting data, calculating probabilities, and making informed decisions based on statistical information.
Exploring Further: Beyond the Basics
The simple problem "What is 1/6 of 120?" opens doors to a deeper understanding of mathematical concepts. Let's explore some related ideas:
- Percentage Calculation: The fraction 1/6 can be easily converted to a percentage: (1/6) * 100% ≈ 16.67%. This means 1/6 of 120 represents approximately 16.67% of 120.
- Ratio and Proportion: The problem can also be viewed as a ratio and proportion problem. If 1/6 of a quantity is 20, what is the whole quantity? This leads to the equation (1/6)x = 20, where x represents the whole quantity (120).
- Algebraic Representation: The problem can be expressed algebraically as (1/n) * x = y, where 'n' is the denominator, 'x' is the whole number, and 'y' is the result. This equation can be used to solve for any of the variables, given the values of the other two.
Frequently Asked Questions (FAQ)
- Q: What if the fraction was more complex, like 5/12 of 120?
A: You would follow the same principles. Either divide 120 by 12 and then multiply by 5, or simplify the fraction if possible before calculating. In this case, 120/12 = 10, and 10 * 5 = 50. So, 5/12 of 120 is 50.
- Q: Can I use a calculator to solve this type of problem?
A: Absolutely! Calculators are helpful tools for more complex fraction problems, but understanding the underlying mathematical concepts remains essential.
- Q: Why is it important to learn about fractions?
A: Understanding fractions is crucial for developing a strong foundation in mathematics. It’s also essential for problem-solving in various real-world applications, as discussed earlier.
Conclusion: The Significance of Fractional Understanding
This article has explored the seemingly simple question, "What is 1/6 of 120?", demonstrating that the solution (20) is just the tip of the iceberg. The process of solving this problem unveils fundamental concepts in fractions, their practical applications, and their importance across various disciplines. Mastering fractions is not merely about performing calculations; it’s about developing a deeper understanding of numerical relationships and their significance in the world around us. By grasping these core concepts, you equip yourself with a valuable skill set applicable far beyond the classroom. From everyday tasks to complex scientific endeavors, the ability to work confidently with fractions is a cornerstone of mathematical proficiency and problem-solving ability.
Latest Posts
Latest Posts
-
4 Divided By 2 3
Sep 23, 2025
-
Vo2 Max Heart Rate Zone
Sep 23, 2025
-
What Is 1 4 Lb
Sep 23, 2025
-
This Day And Age Meaning
Sep 23, 2025
-
5 Is What Of 40
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about What Is 1/6 Of 120 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.