What Is 2/3 Of 35
saludintensiva
Sep 22, 2025 · 6 min read
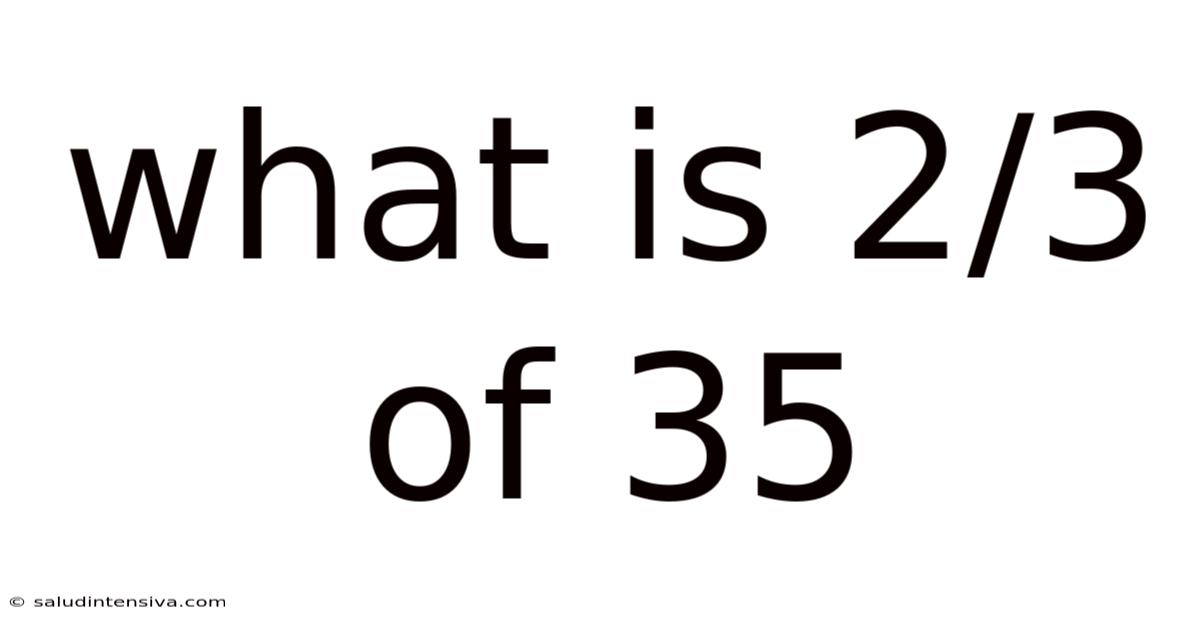
Table of Contents
What is 2/3 of 35? A Comprehensive Guide to Fractions and Multiplication
Finding 2/3 of 35 might seem like a simple arithmetic problem, but it opens a door to understanding fundamental concepts in mathematics, particularly fractions and their application in real-world scenarios. This comprehensive guide will not only provide the answer but also delve deeper into the underlying principles, exploring different methods of calculation, offering practical examples, and addressing common misconceptions. This will equip you with a robust understanding of fractions and their manipulation.
Understanding Fractions: The Building Blocks
Before we tackle the problem of finding 2/3 of 35, let's solidify our understanding of fractions. A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). The numerator indicates how many parts we have, while the denominator indicates how many equal parts the whole is divided into.
For example, in the fraction 2/3, 2 is the numerator and 3 is the denominator. This means we have 2 parts out of a total of 3 equal parts. Understanding this fundamental concept is crucial for any further manipulation of fractions.
Method 1: Converting the Fraction to a Decimal
One way to solve "what is 2/3 of 35?" is to first convert the fraction 2/3 into a decimal. We do this by dividing the numerator (2) by the denominator (3):
2 ÷ 3 = 0.666... (This is a recurring decimal)
For practical purposes, we can round this to a certain number of decimal places. Let's use two decimal places: 0.67.
Now, we multiply this decimal by 35:
0.67 x 35 = 23.45
Therefore, using this method, 2/3 of 35 is approximately 23.45. Remember that this is an approximation due to rounding the decimal representation of 2/3.
Method 2: Multiplying the Fraction Directly
A more precise method involves multiplying the fraction directly by the whole number. To do this, we multiply the numerator of the fraction by the whole number, and then divide the result by the denominator.
(2/3) x 35 = (2 x 35) / 3 = 70 / 3
Now, we perform the division:
70 ÷ 3 = 23.333... (Another recurring decimal)
Again, we have a recurring decimal. This confirms that 2/3 of 35 is not a whole number. Depending on the context, you might round this to 23.33. This method, unlike the decimal conversion method, provides a more accurate result without early rounding.
Method 3: Finding a Fraction of a Whole Number Using Proportions
We can also approach this problem using the concept of proportions. We can set up a proportion to solve for the unknown value, which is 2/3 of 35.
Let's represent the unknown value as 'x'. We can set up the proportion as follows:
2/3 = x/35
To solve for 'x', we cross-multiply:
3x = 2 * 35
3x = 70
x = 70/3
x = 23.333...
This method again leads us to the same recurring decimal result, highlighting the consistency of the mathematical approach.
Real-World Applications: Where Fractions Matter
Understanding how to find a fraction of a number has numerous practical applications in everyday life. Here are a few examples:
- Cooking and Baking: Recipes often require fractions of ingredients. If a recipe calls for 2/3 of a cup of flour, you'll need to know how to measure that accurately.
- Shopping and Discounts: Sales often advertise discounts as fractions, such as "1/3 off." Being able to calculate these discounts helps you determine the final price.
- Construction and Measurement: Construction projects frequently use fractional measurements. Accurate calculations are vital to ensure precision.
- Data Analysis: Understanding fractions is critical when working with percentages and proportions in data analysis and statistics. It's fundamental to interpreting data accurately.
- Sharing and Dividing: Imagine dividing a pizza among friends. Determining fair shares often involves calculating fractions.
Addressing Common Misconceptions
Several common misconceptions can arise when working with fractions:
- Thinking Fractions are Always Smaller than 1: While many fractions are less than 1 (like 2/3), it's essential to remember that improper fractions (where the numerator is larger than the denominator, e.g., 5/2) represent values greater than 1.
- Incorrectly Multiplying Fractions: Remember that when multiplying a fraction by a whole number, you multiply the numerator by the whole number and then divide by the denominator.
- Rounding Errors: Rounding off decimals too early can lead to inaccuracies in the final result. It's always best to carry out calculations with as much precision as possible before rounding.
Frequently Asked Questions (FAQ)
Q: What is the most accurate way to calculate 2/3 of 35?
A: The most accurate way is to multiply the fraction directly (Method 2), avoiding premature rounding. This results in 70/3 or 23.333... (a recurring decimal).
Q: Can I use a calculator to solve this?
A: Yes, a calculator can be used to convert the fraction to a decimal and then multiply by 35. However, it's essential to understand the underlying mathematical principles.
Q: Why is the answer a recurring decimal?
A: The answer is a recurring decimal because the fraction 2/3 is a rational number with a denominator (3) that cannot be expressed as a power of 2 or 5. This means its decimal representation is non-terminating and repeating.
Q: What if the question was "What is 3/2 of 35?"
A: In this case, you would follow the same methods, but the result would be greater than 35 because 3/2 is greater than 1. (3/2) * 35 = (3*35)/2 = 105/2 = 52.5
Q: How can I improve my skills in working with fractions?
A: Practice is key! Work through various problems, starting with simpler ones and gradually increasing the complexity. Use online resources, textbooks, or educational apps to reinforce your understanding.
Conclusion: Mastering Fractions for a Brighter Future
Finding 2/3 of 35 might seem like a small calculation, but understanding the process reveals the power of fractions in mathematics and their widespread application in real-world scenarios. By mastering the techniques outlined in this guide—converting fractions to decimals, direct multiplication, and using proportions—you build a solid foundation for more advanced mathematical concepts. Remember that precision, understanding the underlying principles, and consistent practice are essential for proficiency in working with fractions. Embrace the challenge, and you'll discover the fascinating world of numbers unfolds before you. This knowledge will not only assist you with everyday calculations but will also significantly improve your problem-solving skills, proving invaluable in academic pursuits and future careers.
Latest Posts
Latest Posts
-
1 1 8 As A Percent
Sep 22, 2025
-
1 189 Divided By 365
Sep 22, 2025
-
Geometric Figure With Equal Angles
Sep 22, 2025
-
90 Days From Aug 1
Sep 22, 2025
-
How To Multiply Pi Fractions
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about What Is 2/3 Of 35 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.