What Is 2/5 Of 3
saludintensiva
Sep 22, 2025 · 6 min read
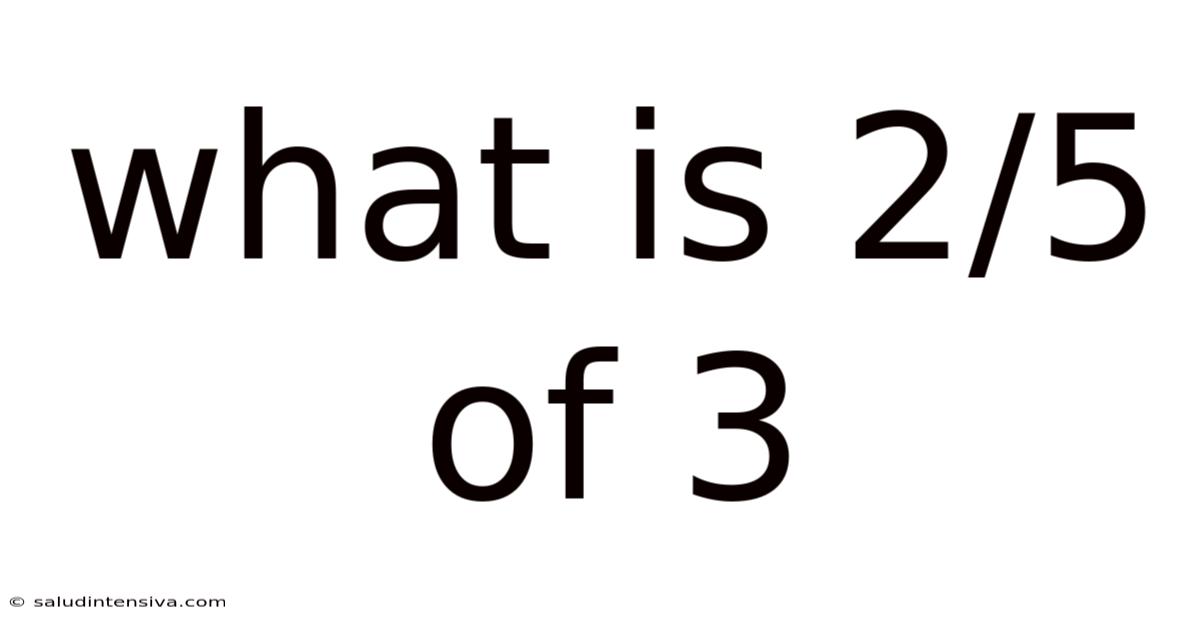
Table of Contents
What is 2/5 of 3? A Deep Dive into Fractions and Multiplication
Finding "2/5 of 3" might seem like a simple arithmetic problem, suitable only for elementary school students. However, understanding this seemingly basic calculation unlocks a deeper understanding of fractions, multiplication, and their real-world applications. This article will not only solve this problem but will also delve into the underlying concepts, providing a comprehensive explanation suitable for learners of all levels. We'll explore different approaches to solving the problem, discuss the underlying mathematical principles, and even touch upon practical applications where this type of calculation is crucial.
Understanding Fractions: The Building Blocks
Before we tackle the problem directly, let's refresh our understanding of fractions. A fraction represents a part of a whole. It's composed of two numbers: the numerator (the top number) and the denominator (the bottom number). The numerator indicates how many parts we have, while the denominator indicates how many equal parts the whole is divided into.
In our problem, "2/5 of 3," 2/5 is the fraction. The numerator is 2, and the denominator is 5. This means we're looking at 2 out of 5 equal parts of something.
Visualizing the Problem
Imagine you have three identical pizzas. To find 2/5 of 3, we need to first divide each pizza into 5 equal slices. This gives us a total of 15 slices (3 pizzas x 5 slices/pizza). Now, we need to take 2 slices from each pizza. Since we have 3 pizzas, we’ll take 2 slices from each, resulting in a total of 6 slices (2 slices/pizza x 3 pizzas). Therefore, 2/5 of 3 is 6/5 or 1 and 1/5.
This visual representation helps solidify the concept, especially for those who find abstract mathematical concepts challenging.
Method 1: Direct Multiplication
The most straightforward method to solve "2/5 of 3" is through direct multiplication. "Of" in mathematics often signifies multiplication. So, we can rewrite the problem as:
(2/5) x 3
To multiply a fraction by a whole number, we can simply multiply the numerator by the whole number and keep the denominator the same:
(2 x 3) / 5 = 6/5
This fraction, 6/5, is an improper fraction because the numerator (6) is larger than the denominator (5). We can convert it into a mixed number:
6/5 = 1 and 1/5
Therefore, 2/5 of 3 is 1 and 1/5.
Method 2: Converting to Decimals
Another approach is to convert the fraction and the whole number into decimals before multiplying.
2/5 as a decimal is 0.4 (2 divided by 5).
Now, multiply 0.4 by 3:
0.4 x 3 = 1.2
This decimal, 1.2, can be converted back into a fraction:
1.2 = 1 and 2/10 = 1 and 1/5
Again, we arrive at the same answer: 1 and 1/5.
Method 3: Breaking Down the Problem
We can also break down the problem into smaller, more manageable parts. We can find 1/5 of 3 first and then multiply the result by 2.
1/5 of 3 is calculated as:
(1/5) x 3 = 3/5
Now, we multiply this result by 2 to find 2/5 of 3:
(3/5) x 2 = 6/5 = 1 and 1/5
This method demonstrates a different approach to problem-solving, emphasizing the flexibility of mathematical operations.
The Importance of Understanding Fractions in Real-Life
The seemingly simple problem of finding "2/5 of 3" has numerous real-world applications. Consider these scenarios:
- Cooking: A recipe calls for 2/5 of a cup of sugar for 3 servings. You need to calculate the total amount of sugar needed.
- Construction: A project requires 3 lengths of wood, each needing to be cut to 2/5 of its original length. Determining the precise cut length is crucial.
- Finance: Calculating discounts, interest rates, and proportions of investments often involves working with fractions.
- Data Analysis: Representing and interpreting data often involves using fractions and percentages, which are closely related concepts.
- Geometry: Finding the area or volume of shapes often requires calculations involving fractions.
These examples highlight that a firm grasp of fraction arithmetic is not just an academic exercise but a vital life skill.
Addressing Common Misconceptions
Many learners struggle with fractions. Some common misconceptions include:
- Incorrectly multiplying numerators and denominators: Some learners might mistakenly multiply both the numerator and the denominator by the whole number, leading to an incorrect answer.
- Difficulty converting between fractions and decimals: The ability to seamlessly switch between fractions and decimals is crucial for solving various problems.
- Confusion with improper fractions and mixed numbers: Understanding the difference between these two forms and how to convert between them is essential.
Overcoming these misconceptions requires consistent practice and a solid understanding of the fundamental principles behind fractions.
Frequently Asked Questions (FAQ)
Q1: Can I solve this problem using a calculator?
A1: Yes, you can. Most calculators allow you to input fractions directly or convert fractions to decimals for calculation. However, understanding the underlying mathematical principles is crucial, even if you use a calculator.
Q2: What if the number wasn't a whole number? What if it was a fraction itself?
A2: If the number was a fraction, you would simply multiply the two fractions together. Remember to multiply the numerators together and the denominators together. For example, to find 2/5 of 3/4, you would calculate (2/5) x (3/4) = 6/20 = 3/10.
Q3: Are there other ways to represent the answer 1 and 1/5?
A3: Yes, the answer can also be represented as a decimal (1.2) or as a percentage (120%). The best representation depends on the context of the problem.
Q4: Why is understanding this type of calculation important?
A4: Understanding fraction multiplication is fundamental to more advanced mathematical concepts and is essential for solving practical problems in various fields, as illustrated in the real-life examples above.
Conclusion: Beyond the Numbers
Finding "2/5 of 3" is more than just a simple arithmetic problem. It's a gateway to understanding the fundamental principles of fractions, multiplication, and their diverse applications. By mastering this seemingly basic calculation, you build a strong foundation for more complex mathematical concepts and develop problem-solving skills applicable to various aspects of life. Remember to practice regularly, visualize the problem whenever possible, and don't hesitate to explore different methods to solidify your understanding. The journey of learning mathematics is about more than just getting the right answer; it's about developing a deeper appreciation for the logic and beauty inherent in the subject. Keep exploring, keep questioning, and keep learning!
Latest Posts
Latest Posts
-
1 1 8 As A Percent
Sep 22, 2025
-
1 189 Divided By 365
Sep 22, 2025
-
Geometric Figure With Equal Angles
Sep 22, 2025
-
90 Days From Aug 1
Sep 22, 2025
-
How To Multiply Pi Fractions
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about What Is 2/5 Of 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.