What Is 3/4 In Percent
saludintensiva
Sep 11, 2025 · 6 min read
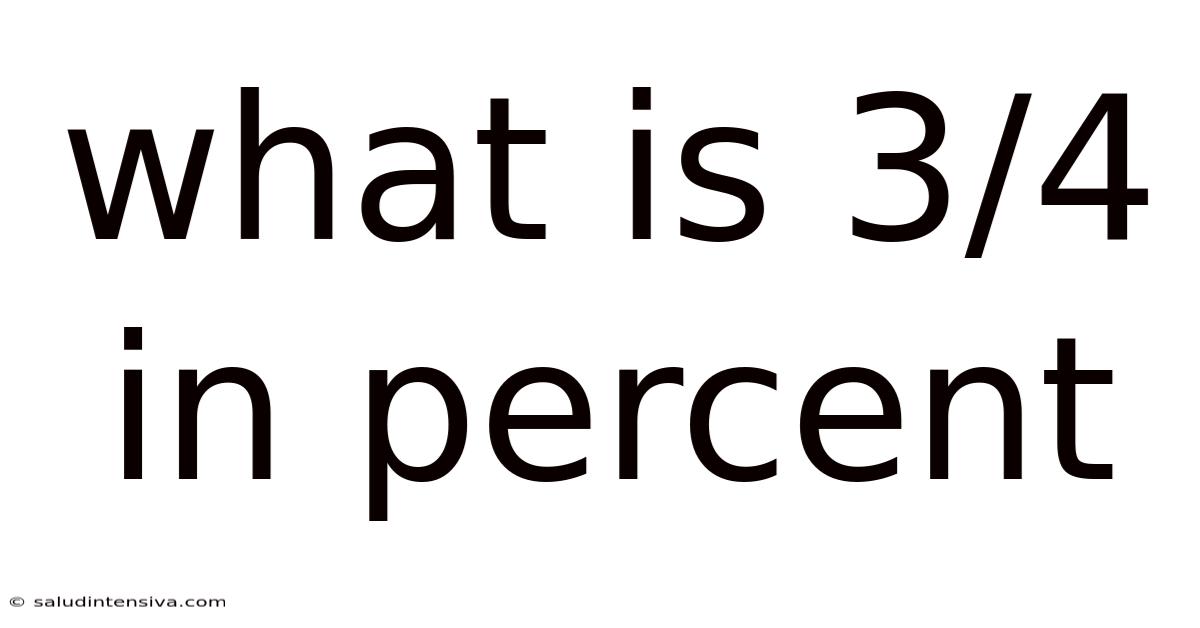
Table of Contents
What is 3/4 in Percent? A Comprehensive Guide to Fraction-to-Percentage Conversion
Understanding fractions and percentages is fundamental to various aspects of life, from calculating discounts in a shop to comprehending data in scientific research. This comprehensive guide will explore the conversion of fractions to percentages, focusing specifically on how to determine what 3/4 is in percent, and providing a broader understanding of the underlying mathematical principles. We'll cover the method, provide examples, and delve into the practical applications of this essential conversion.
Understanding Fractions and Percentages
Before we dive into the specific conversion of 3/4, let's establish a strong foundation. A fraction represents a part of a whole. It consists of a numerator (the top number) and a denominator (the bottom number). The numerator indicates the number of parts you have, and the denominator indicates the total number of parts in the whole.
A percentage, on the other hand, represents a fraction out of 100. The word "percent" literally means "out of 100" (from the Latin per centum). Therefore, a percentage expresses a proportion as a fraction of 100. For instance, 50% means 50 out of 100, which is equivalent to the fraction 50/100, or simplified, 1/2.
Converting Fractions to Percentages: The Method
The core process of converting a fraction to a percentage involves two simple steps:
- Convert the fraction to a decimal: Divide the numerator by the denominator.
- Convert the decimal to a percentage: Multiply the decimal by 100 and add the "%" symbol.
Let's illustrate this with a simple example: Convert 1/2 to a percentage.
- Decimal conversion: 1 ÷ 2 = 0.5
- Percentage conversion: 0.5 × 100 = 50%
Therefore, 1/2 is equal to 50%.
Calculating 3/4 as a Percentage
Now, let's apply this method to determine what 3/4 is in percent:
- Decimal conversion: 3 ÷ 4 = 0.75
- Percentage conversion: 0.75 × 100 = 75%
Therefore, 3/4 is equal to 75%. This is a commonly used fraction and percentage, often encountered in everyday life and various applications.
Visualizing 3/4 and 75%
To further solidify the understanding, let's visualize this. Imagine a pizza cut into four equal slices. 3/4 represents three out of those four slices. 75% also represents three out of four slices, because 75 out of 100 is equivalent to 3 out of 4 (simplified). This visual representation helps to connect the abstract concept of fractions and percentages to a tangible reality.
Practical Applications of 3/4 and 75%
The equivalence of 3/4 and 75% has numerous practical applications across various fields:
- Retail Sales: Discounts are frequently expressed as percentages. A 75% discount means you pay only 25% of the original price. This is equivalent to receiving 3/4 off the original price.
- Data Analysis: When analyzing data presented in fractions, converting them to percentages can make the information easier to interpret and compare. For example, if 3/4 of a survey's respondents agreed with a statement, this translates to a strong 75% agreement rate.
- Cooking and Baking: Recipes often use fractions to represent ingredient quantities. Understanding the percentage equivalent can help with scaling recipes up or down. For example, if a recipe calls for 3/4 cup of flour, it's the same as 75% of a cup.
- Construction and Engineering: Measurements and proportions in construction frequently involve fractions. Converting these to percentages can aid in calculations and comparisons. For example, a beam might be 3/4 of the required length, which is 75% of the needed length.
- Financial Calculations: Understanding percentages is crucial for analyzing financial data. Interest rates, investment returns, and loan calculations often involve percentage conversions from fractions.
Further Exploring Fraction-to-Percentage Conversions
The method described above applies to all fractions. Let's look at a few more examples:
- 1/4: 1 ÷ 4 = 0.25; 0.25 × 100 = 25%
- 1/2: 1 ÷ 2 = 0.5; 0.5 × 100 = 50%
- 2/3: 2 ÷ 3 ≈ 0.667; 0.667 × 100 ≈ 66.7% (Note the approximate value due to the repeating decimal)
- 5/8: 5 ÷ 8 = 0.625; 0.625 × 100 = 62.5%
These examples showcase the versatility of the conversion method. Regardless of the complexity of the fraction, the principle remains the same: divide the numerator by the denominator and then multiply the result by 100.
Handling Mixed Numbers
A mixed number combines a whole number and a fraction (e.g., 1 1/2). To convert a mixed number to a percentage, first convert it into an improper fraction and then follow the steps outlined above.
For example, let's convert 1 1/2 to a percentage:
- Convert to an improper fraction: 1 1/2 = (1 × 2 + 1) / 2 = 3/2
- Decimal conversion: 3 ÷ 2 = 1.5
- Percentage conversion: 1.5 × 100 = 150%
Dealing with Decimals in Fractions
Sometimes, you might encounter fractions with decimal numbers in the numerator or denominator. The process remains similar, but you need to be extra careful with the calculations. For example, let's convert 0.75/2 to a percentage:
- Decimal conversion: 0.75 ÷ 2 = 0.375
- Percentage conversion: 0.375 × 100 = 37.5%
Frequently Asked Questions (FAQ)
Q: Why is it important to understand fraction-to-percentage conversion?
A: This conversion is crucial for various aspects of life, from everyday calculations to advanced mathematical and scientific applications. It allows for easier comparison and understanding of proportions.
Q: Can I convert any fraction to a percentage?
A: Yes, any fraction, including mixed numbers and fractions with decimals, can be converted to a percentage using the methods described above.
Q: What if the decimal result is a repeating decimal?
A: For repeating decimals, you can either round the decimal to a reasonable number of significant figures or express it as a fraction.
Q: Are there any online tools or calculators for this conversion?
A: While many online tools are available, understanding the underlying method is far more beneficial for long-term learning and application.
Q: Can I convert percentages back to fractions?
A: Absolutely! To convert a percentage to a fraction, divide the percentage by 100 and simplify the resulting fraction. For example, 75% = 75/100 = 3/4.
Conclusion
Converting fractions to percentages is a fundamental mathematical skill with broad applications. This guide has provided a thorough explanation of the process, focusing specifically on converting 3/4 to 75%. Through numerous examples and a breakdown of the steps, we've aimed to build a strong understanding of this vital conversion and its practical relevance across various fields. Remember, the key is to master the fundamental principles of fraction and percentage representation to confidently tackle any conversion task. By understanding this concept, you'll be better equipped to handle various mathematical and real-world problems requiring proportional calculations. The ability to seamlessly convert between fractions and percentages empowers you to interpret and analyze data more effectively, ultimately enhancing your problem-solving skills in various contexts.
Latest Posts
Latest Posts
-
What Is Equivalent To 3 6
Sep 11, 2025
-
Gpa Converter To 5 0 Scale
Sep 11, 2025
-
Gcf For 12 And 28
Sep 11, 2025
-
90 Days From 6 19
Sep 11, 2025
-
Equivalent Fractions To 8 10
Sep 11, 2025
Related Post
Thank you for visiting our website which covers about What Is 3/4 In Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.