What Is 3/6 Equal To
saludintensiva
Sep 13, 2025 · 6 min read
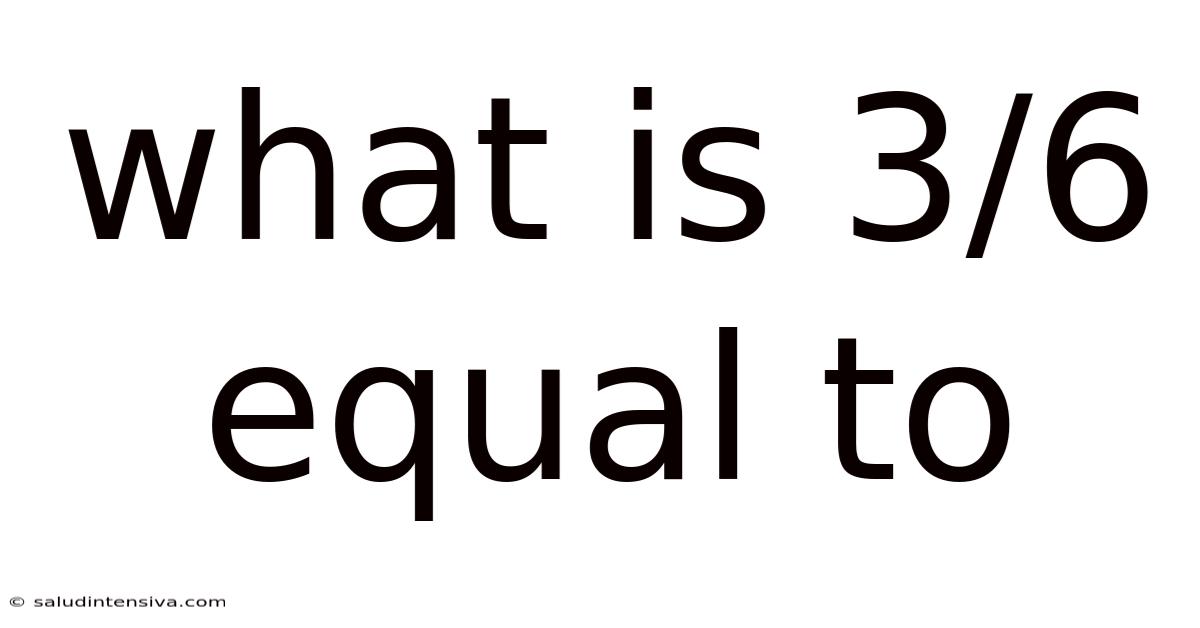
Table of Contents
What is 3/6 Equal To? A Deep Dive into Fractions and Simplification
Understanding fractions is fundamental to mathematics and numerous real-world applications. This comprehensive guide will explore the question, "What is 3/6 equal to?" We'll delve into the concept of equivalent fractions, fraction simplification, and demonstrate why understanding this seemingly simple equation is crucial for building a strong mathematical foundation. We'll also touch upon practical examples to show the relevance of fraction simplification in everyday life.
Understanding Fractions: The Basics
A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). The denominator shows the total number of equal parts the whole is divided into, while the numerator indicates how many of those parts are being considered. In the fraction 3/6, 3 is the numerator and 6 is the denominator. This means we are considering 3 parts out of a total of 6 equal parts.
Finding Equivalent Fractions: The Core Concept
Equivalent fractions represent the same value even though they look different. They are different ways of expressing the same portion of a whole. To find an equivalent fraction, you multiply or divide both the numerator and the denominator by the same non-zero number. This is because multiplying or dividing both parts of a fraction by the same number is essentially multiplying or dividing by 1 (e.g., 2/2 = 1, 5/5 = 1). This doesn't change the overall value.
For example, let's consider the fraction 1/2. If we multiply both the numerator and the denominator by 2, we get 2/4. Both 1/2 and 2/4 represent exactly half of a whole. Similarly, multiplying by 3 gives us 3/6, multiplying by 4 gives 4/8, and so on. All these fractions are equivalent to 1/2.
Simplifying Fractions: Reducing to Lowest Terms
Simplifying a fraction means reducing it to its simplest form, also known as expressing it in its lowest terms. This involves finding the greatest common divisor (GCD) or greatest common factor (GCF) of the numerator and the denominator and then dividing both by that number. The GCD is the largest number that divides both the numerator and denominator without leaving a remainder.
Let's apply this to our original question: What is 3/6 equal to?
-
Find the GCD of 3 and 6: The factors of 3 are 1 and 3. The factors of 6 are 1, 2, 3, and 6. The greatest common factor is 3.
-
Divide both the numerator and the denominator by the GCD: Dividing both 3 and 6 by 3, we get:
3 ÷ 3 = 1 6 ÷ 3 = 2
Therefore, 3/6 simplified is 1/2.
Visual Representation: Understanding the Equivalence
Visual aids can significantly enhance understanding. Imagine a pizza cut into 6 equal slices. If you eat 3 slices, you've eaten 3/6 of the pizza. However, if we group the 6 slices into pairs, we see that we've eaten 1 out of 2 pairs. This visually demonstrates that 3/6 is equivalent to 1/2. The same applies to any scenario divisible into equal parts – a chocolate bar, a pie, or even a group of objects.
Practical Applications: Why Simplification Matters
Simplifying fractions isn't just a mathematical exercise; it's crucial for several reasons:
-
Clarity and Understanding: Simplified fractions are easier to understand and compare. It's much easier to grasp the concept of 1/2 than 3/6, especially when dealing with more complex calculations or comparisons.
-
Efficiency in Calculations: Working with simplified fractions makes calculations significantly faster and less prone to errors. Imagine multiplying 3/6 by another fraction; the calculation is simpler if you use the equivalent 1/2.
-
Real-World Problem Solving: Many everyday situations involve fractions – sharing food, measuring ingredients, understanding discounts, or calculating proportions. Simplifying fractions allows for easier comprehension and quicker solutions. For example, if a recipe calls for 3/6 of a cup of sugar, knowing that it's equivalent to 1/2 a cup simplifies the measuring process.
-
Data Analysis and Interpretation: In fields like data science and statistics, simplified fractions are essential for clear presentation and interpretation of results.
Beyond 3/6: Extending the Concept
The process of simplifying fractions applies to all fractions. Let's consider some examples:
-
6/8: The GCD of 6 and 8 is 2. Dividing both by 2 simplifies the fraction to 3/4.
-
12/15: The GCD of 12 and 15 is 3. Dividing both by 3 simplifies the fraction to 4/5.
-
15/25: The GCD of 15 and 25 is 5. Dividing both by 5 simplifies the fraction to 3/5.
Improper Fractions and Mixed Numbers
Sometimes, you encounter improper fractions where the numerator is larger than or equal to the denominator (e.g., 7/4). These can be converted into mixed numbers, which combine a whole number and a fraction (e.g., 1 ¾). Simplifying an improper fraction before converting it to a mixed number often streamlines the process.
Frequently Asked Questions (FAQ)
-
Q: Can I simplify a fraction by only dividing the numerator? A: No. To maintain the value of the fraction, you must divide both the numerator and the denominator by the same number.
-
Q: What if the GCD of the numerator and denominator is 1? A: The fraction is already in its simplest form. It cannot be simplified further.
-
Q: Are there different methods for simplifying fractions? A: While the GCD method is the most efficient, you can also simplify step-by-step by dividing by common factors until you reach the lowest terms.
-
Q: Why is it important to learn about equivalent fractions and simplification? A: These concepts are fundamental for building a strong understanding of fractions, which are essential for more advanced mathematical concepts and real-world problem-solving.
Conclusion: Mastering Fractions for a Brighter Future
This comprehensive exploration of the seemingly simple question, "What is 3/6 equal to?" has revealed the importance of understanding equivalent fractions and the process of simplification. It's not just about getting the right answer; it's about developing a deeper understanding of fractions and their applications. Mastering these concepts builds a solid foundation for future mathematical endeavors and equips you with essential skills for various aspects of life. Remember, practice is key! The more you work with fractions, the more confident and proficient you'll become in simplifying them and applying this knowledge to solve various problems. From baking a cake to understanding financial statements, the ability to work confidently with fractions is a valuable asset.
Latest Posts
Latest Posts
-
Least To Greatest Calculator Decimals
Sep 13, 2025
-
19 50 As A Decimal
Sep 13, 2025
-
2 7 As A Decimal
Sep 13, 2025
-
What Is 2 2 Simplified
Sep 13, 2025
-
Lowest Term Of 5 20
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about What Is 3/6 Equal To . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.