What Is Equal To 10/12
saludintensiva
Sep 12, 2025 · 5 min read
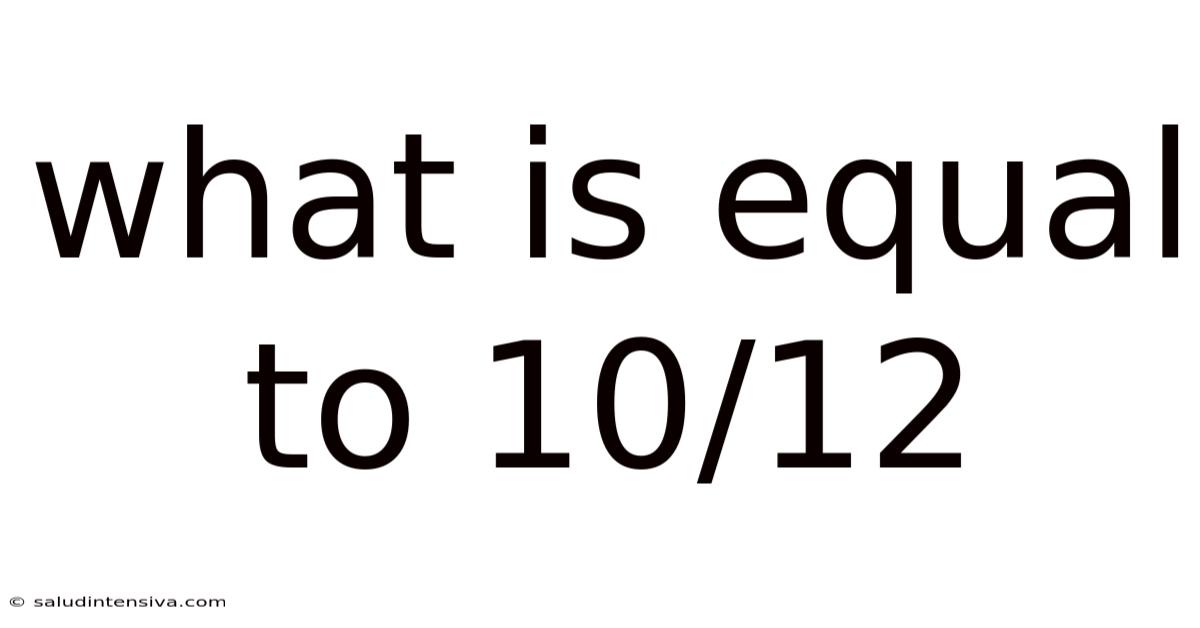
Table of Contents
What is Equal to 10/12? A Deep Dive into Fractions, Simplification, and Equivalent Fractions
Finding out what's equal to 10/12 might seem like a simple question, but it opens the door to a deeper understanding of fractions, a fundamental concept in mathematics. This article will explore the meaning of 10/12, how to simplify it to its lowest terms, and how to find other equivalent fractions. We'll delve into the underlying principles, providing a comprehensive explanation suitable for learners of all levels.
Introduction: Understanding Fractions
A fraction represents a part of a whole. It's written as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). In the fraction 10/12, 10 is the numerator and 12 is the denominator. This means we're considering 10 parts out of a total of 12 equal parts. Understanding fractions is crucial in various fields, from baking and cooking to engineering and finance.
Simplifying 10/12: Finding the Lowest Terms
The fraction 10/12 isn't in its simplest form. Simplifying a fraction means reducing it to its equivalent form where the numerator and denominator have no common factors other than 1. To simplify, we need to find the greatest common divisor (GCD) of the numerator (10) and the denominator (12).
The GCD is the largest number that divides both 10 and 12 without leaving a remainder. We can find the GCD using several methods:
-
Listing Factors: The factors of 10 are 1, 2, 5, and 10. The factors of 12 are 1, 2, 3, 4, 6, and 12. The greatest common factor is 2.
-
Prime Factorization: We break down each number into its prime factors.
- 10 = 2 x 5
- 12 = 2 x 2 x 3 = 2² x 3 The common prime factor is 2. Therefore, the GCD is 2.
Once we've found the GCD (which is 2), we divide both the numerator and the denominator by this number:
10 ÷ 2 = 5 12 ÷ 2 = 6
Therefore, the simplified form of 10/12 is 5/6. This means 10/12 and 5/6 represent the same value; they are equivalent fractions.
Equivalent Fractions: Infinite Possibilities
Equivalent fractions are fractions that represent the same value, even though they look different. We can create an infinite number of equivalent fractions by multiplying or dividing both the numerator and the denominator by the same non-zero number.
For example, let's find some equivalent fractions to 5/6:
- Multiplying both by 2: (5 x 2) / (6 x 2) = 10/12 (This brings us back to our original fraction!)
- Multiplying both by 3: (5 x 3) / (6 x 3) = 15/18
- Multiplying both by 4: (5 x 4) / (6 x 4) = 20/24
- Multiplying both by 5: (5 x 5) / (6 x 5) = 25/30
- And so on...
We can also create equivalent fractions by dividing (if possible). However, 5/6 is already in its simplest form, so we can only create larger equivalent fractions through multiplication.
Visual Representation: Understanding Fractions Geometrically
Visualizing fractions can make the concept much clearer. Imagine a pizza cut into 12 equal slices. 10/12 represents 10 of those slices. If we group the slices into pairs, we'll have 5 pairs out of a total of 6 pairs. This visually demonstrates that 10/12 is equivalent to 5/6.
Similarly, we can represent 5/6 using a rectangle divided into 6 equal parts, shading 5 of them. We could then divide each of those parts further to create equivalent fractions like 10/12, 15/18, and so on. Each representation shows the same proportional amount.
Decimal Equivalent: Converting Fractions to Decimals
Fractions can also be expressed as decimals. To convert 10/12 (or its simplified form 5/6) to a decimal, we perform the division:
5 ÷ 6 ≈ 0.8333...
The decimal representation is a repeating decimal, indicated by the ellipsis (...). This means the digit 3 repeats infinitely. Often, we round the decimal to a certain number of decimal places for practical purposes, for instance, 0.83.
Applications of Fractions in Real Life:
Fractions are integral to many aspects of daily life:
- Cooking and Baking: Recipes often use fractions (e.g., ½ cup of sugar, ¾ cup of flour).
- Shopping: Discounts are often expressed as fractions (e.g., ⅓ off).
- Construction and Engineering: Precise measurements and calculations rely heavily on fractions.
- Finance: Understanding fractions is essential for calculating interest rates, proportions, and other financial concepts.
Frequently Asked Questions (FAQ)
-
Q: Is 10/12 a proper or improper fraction?
- A: 10/12 is a proper fraction because the numerator (10) is smaller than the denominator (12). An improper fraction has a numerator greater than or equal to the denominator.
-
Q: How can I simplify fractions quickly?
- A: The quickest method is to find the greatest common divisor (GCD) of the numerator and denominator and divide both by the GCD. Using prime factorization can be particularly helpful for larger numbers.
-
Q: Are there any other methods to find equivalent fractions besides multiplying or dividing by the same number?
- A: No, multiplying or dividing both the numerator and the denominator by the same non-zero number is the fundamental method for generating equivalent fractions.
-
Q: Why is simplifying fractions important?
- A: Simplifying fractions makes them easier to understand and work with. It also provides a clearer representation of the value. In many mathematical operations, working with simplified fractions leads to simpler calculations and avoids unnecessary complexity.
Conclusion: Mastering Fractions
Understanding what is equal to 10/12 involves more than just a simple calculation; it’s a gateway to grasping the essence of fractions. We’ve explored simplifying fractions, identifying equivalent fractions, and visualized these concepts geometrically. This knowledge is not just important for academic success but also crucial for navigating everyday tasks and solving real-world problems. By mastering the concepts outlined here, you'll build a solid foundation in mathematics and enhance your problem-solving skills across numerous disciplines. Remember, practice is key! The more you work with fractions, the more intuitive they become.
Latest Posts
Latest Posts
-
2000 Sq Ft To Meters
Sep 12, 2025
-
61 3 Percent Of 60 Questions
Sep 12, 2025
-
What Was 21 Weeks Ago
Sep 12, 2025
-
How To Simplify Big Fractions
Sep 12, 2025
-
Gcf Of 40 And 72
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about What Is Equal To 10/12 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.