What Is Equivalent To 5/6
saludintensiva
Sep 09, 2025 · 6 min read
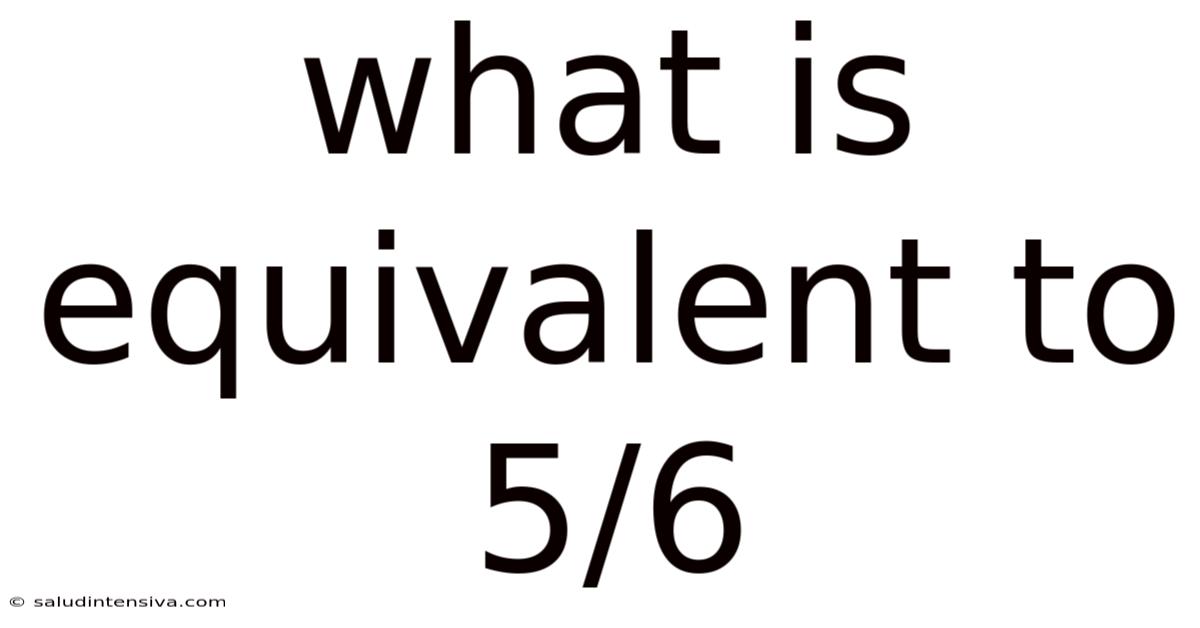
Table of Contents
What is Equivalent to 5/6? Exploring Fractions and Equivalence
Finding equivalent fractions is a fundamental concept in mathematics, crucial for understanding proportions, ratios, and simplifying complex calculations. This article dives deep into the concept of fractional equivalence, specifically exploring what fractions are equivalent to 5/6. We'll cover the core principles, practical methods for finding equivalents, and delve into the broader mathematical context. Understanding this will solidify your grasp of fractions and open doors to more advanced mathematical concepts.
Understanding Fractions and Equivalence
Before we jump into finding equivalents for 5/6, let's establish a solid foundation. A fraction represents a part of a whole. It's written as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). The denominator indicates how many equal parts the whole is divided into, while the numerator indicates how many of those parts are being considered.
Equivalent fractions represent the same proportion or value, even though they look different. This means they represent the same point on a number line. We obtain equivalent fractions by multiplying or dividing both the numerator and the denominator by the same non-zero number. This is because multiplying or dividing both parts by the same number doesn't change the overall ratio. Think of it like enlarging or shrinking a picture – the proportions remain the same.
For example, 1/2 is equivalent to 2/4, 3/6, 4/8, and so on. In each case, we've multiplied both the numerator and the denominator by the same number (2, 3, 4, respectively). Similarly, we can obtain equivalent fractions by dividing; for example, 6/9 is equivalent to 2/3 (dividing both by 3).
Finding Equivalent Fractions to 5/6: A Step-by-Step Approach
Now, let's explore how to find fractions equivalent to 5/6. The process is simple: multiply both the numerator (5) and the denominator (6) by the same number. Let's generate several examples:
- Multiplying by 2: (5 x 2) / (6 x 2) = 10/12
- Multiplying by 3: (5 x 3) / (6 x 3) = 15/18
- Multiplying by 4: (5 x 4) / (6 x 4) = 20/24
- Multiplying by 5: (5 x 5) / (6 x 5) = 25/30
- Multiplying by 10: (5 x 10) / (6 x 10) = 50/60
- Multiplying by 100: (5 x 100) / (6 x 100) = 500/600
As you can see, there are infinitely many fractions equivalent to 5/6. We can generate as many as we need simply by multiplying both the numerator and the denominator by any non-zero whole number.
Simplifying Fractions: Finding the Simplest Equivalent
While we can create countless equivalent fractions by multiplication, it's often useful to find the simplest equivalent fraction. This is done by finding the greatest common divisor (GCD) of the numerator and the denominator and then dividing both by that GCD. The GCD is the largest number that divides both the numerator and the denominator without leaving a remainder.
Let's consider the fraction 10/12. The factors of 10 are 1, 2, 5, and 10. The factors of 12 are 1, 2, 3, 4, 6, and 12. The greatest common factor of 10 and 12 is 2. Dividing both the numerator and denominator by 2 gives us 5/6, which is the simplest form of 10/12.
In the case of 5/6, the greatest common divisor of 5 and 6 is 1. This means that 5/6 is already in its simplest form; we cannot simplify it further.
Visualizing Equivalent Fractions
Visual aids can greatly enhance understanding. Imagine a pizza cut into 6 slices. If you eat 5 slices, you've eaten 5/6 of the pizza. Now imagine the same pizza, but cut into 12 slices. Eating 10 slices (10/12) is the same as eating 5 out of 6 slices. Both 5/6 and 10/12 represent the same amount of pizza consumed. This visual representation clearly demonstrates the concept of equivalent fractions. You can apply this visual analogy to various scenarios involving parts of a whole.
Equivalent Fractions in Real-World Applications
The concept of equivalent fractions isn't just confined to theoretical mathematics; it has numerous practical applications:
-
Baking and Cooking: Recipes often require adjusting ingredient amounts based on the number of servings. Equivalent fractions are crucial for maintaining the correct proportions. If a recipe calls for 5/6 of a cup of flour, and you want to double the recipe, you'll need 10/12 (or simplified, 5/6) of a cup.
-
Measurement and Scale: Maps, blueprints, and scale models utilize fractions extensively. Understanding equivalent fractions allows for accurate scaling and interpretation of measurements.
-
Finance and Budgeting: Percentages, which are essentially fractions with a denominator of 100, are fundamental to personal finance and business calculations. Equivalent fractions help in comparing different proportions of income and expenditure.
-
Data Analysis and Probability: Equivalent fractions play a critical role in representing probabilities and proportions in data analysis. Simplifying fractions often makes interpreting the results much easier.
Beyond Simple Fractions: Decimals and Percentages
It's important to understand that equivalent representations aren't limited to just fractions. 5/6 can also be expressed as a decimal and a percentage:
-
Decimal: To convert 5/6 to a decimal, divide the numerator (5) by the denominator (6). This results in 0.8333... (a repeating decimal).
-
Percentage: To convert 5/6 to a percentage, multiply the decimal equivalent by 100. This gives approximately 83.33%.
These equivalent representations offer alternative ways to express the same value, each useful in different contexts.
Frequently Asked Questions (FAQ)
Q: Are there any fractions equivalent to 5/6 that have a denominator larger than 600?
A: Yes, infinitely many. You can obtain equivalent fractions by multiplying both the numerator and the denominator by any number greater than 100.
Q: How can I quickly determine if two fractions are equivalent?
A: Cross-multiply the numerators and denominators. If the products are equal, the fractions are equivalent. For example, to check if 5/6 and 10/12 are equivalent, multiply 5 x 12 (60) and 6 x 10 (60). Since the products are equal, the fractions are equivalent.
Q: Why is simplifying fractions important?
A: Simplifying fractions makes them easier to understand, compare, and use in calculations. Working with smaller numbers is generally simpler and reduces the chance of errors.
Q: Can a fraction have more than one simplest equivalent form?
A: No. Every fraction has only one simplest equivalent form, which is obtained by dividing both the numerator and the denominator by their greatest common divisor.
Conclusion: Mastering the Art of Equivalent Fractions
Understanding equivalent fractions is a cornerstone of mathematical literacy. This article explored the concept in detail, focusing specifically on finding fractions equivalent to 5/6. We covered various methods, from simple multiplication to finding the simplest form, and highlighted the practical applications in diverse fields. By mastering the art of finding and recognizing equivalent fractions, you'll enhance your problem-solving abilities and gain a deeper appreciation for the elegance and practicality of mathematics. Remember, the key lies in understanding the fundamental principle: multiplying or dividing both the numerator and the denominator by the same non-zero number maintains the value of the fraction, creating an equivalent representation. Keep practicing, and you'll soon be comfortable navigating the world of fractions with confidence!
Latest Posts
Latest Posts
-
Convert 84 F To C
Sep 09, 2025
-
Gcf Of 40 And 48
Sep 09, 2025
-
10 Percent In A Fraction
Sep 09, 2025
-
Standard Deviation In R Studio
Sep 09, 2025
-
Square Root Of 10 000
Sep 09, 2025
Related Post
Thank you for visiting our website which covers about What Is Equivalent To 5/6 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.