Whats Bigger 1/8 Or 3/16
saludintensiva
Sep 18, 2025 · 5 min read
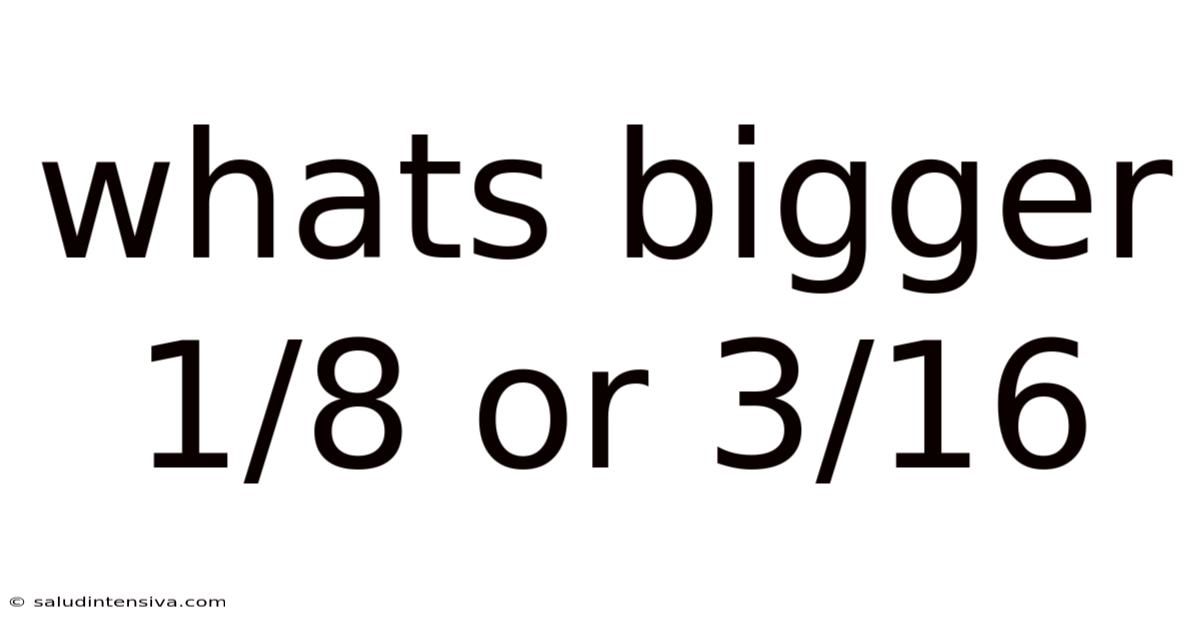
Table of Contents
What's Bigger: 1/8 or 3/16? Understanding Fractions and Comparisons
This article will delve into the seemingly simple question: what's bigger, 1/8 or 3/16? While the answer might seem obvious to some, understanding the underlying principles of comparing fractions is crucial for developing strong mathematical skills. We'll explore various methods for comparing fractions, explain the logic behind the solution, and provide practical examples to solidify your understanding. This comprehensive guide will equip you with the tools to tackle similar fraction comparisons confidently.
Introduction: A Quick Refresher on Fractions
Before we dive into the comparison, let's refresh our understanding of fractions. A fraction represents a part of a whole. It's written as a/b, where 'a' is the numerator (the number of parts we have) and 'b' is the denominator (the total number of equal parts the whole is divided into). For instance, in the fraction 1/8, 1 is the numerator and 8 is the denominator, representing one out of eight equal parts.
Understanding fractions is fundamental to various aspects of life, from baking and cooking (measuring ingredients) to construction (measuring materials) and even finance (understanding percentages and proportions). Mastering fraction comparison is key to mastering these applications.
Method 1: Finding a Common Denominator
The most common and reliable method for comparing fractions is to find a common denominator. This means finding a number that both denominators (8 and 16 in this case) can divide into evenly. In this example, 16 is a common denominator because 8 x 2 = 16.
- Converting 1/8: To convert 1/8 to a fraction with a denominator of 16, we multiply both the numerator and the denominator by 2: (1 x 2) / (8 x 2) = 2/16.
Now we can easily compare:
- 2/16 vs. 3/16
Since both fractions have the same denominator, we simply compare the numerators. 3 is greater than 2, therefore:
- 3/16 is bigger than 1/8.
Method 2: Visual Representation
Visual aids can significantly enhance understanding, especially when dealing with abstract concepts like fractions. Imagine a pizza cut into 8 equal slices (representing 1/8) and another pizza cut into 16 equal slices (representing 3/16).
If you take one slice from the first pizza (1/8), you have a relatively large portion. However, if you take three slices from the second pizza (3/16), you'll notice you have a slightly larger portion than the single slice from the first pizza. This visual representation confirms that 3/16 is larger than 1/8.
Method 3: Converting to Decimals
Another way to compare fractions is to convert them into decimals. This involves dividing the numerator by the denominator.
-
1/8 as a decimal: 1 ÷ 8 = 0.125
-
3/16 as a decimal: 3 ÷ 16 = 0.1875
By comparing the decimal values, we see that 0.1875 is greater than 0.125, confirming that:
- 3/16 is bigger than 1/8.
Understanding the Logic: Why This Method Works
The success of the common denominator method lies in the fact that it allows for a direct comparison of the relative sizes of the parts. By expressing both fractions with the same denominator, we're essentially comparing the same-sized "chunks" of the whole. The fraction with the larger numerator represents a larger portion of the whole.
Converting to decimals works because decimals offer a standardized way of representing parts of a whole. The decimal representation directly reflects the magnitude of the fraction, making comparison straightforward.
Beyond the Basics: Comparing More Complex Fractions
The methods discussed above can be extended to compare more complex fractions. For example, let's compare 5/12 and 7/18. Finding a common denominator (36) and converting gives us:
-
5/12 = 15/36
-
7/18 = 14/36
Therefore, 5/12 is larger than 7/18.
Similarly, converting to decimals:
-
5/12 ≈ 0.4167
-
7/18 ≈ 0.3889
Again, confirming that 5/12 is greater.
Practical Applications: Real-World Examples
Understanding fraction comparison is crucial in numerous real-world scenarios:
-
Baking: Recipes often require precise measurements of ingredients. Comparing fractions helps ensure the correct proportions are used.
-
Construction: Accurate measurements are vital in construction projects. Comparing fractions helps ensure materials are cut to the correct sizes.
-
Finance: Understanding proportions and percentages (which are essentially fractions) is vital for managing personal finances, investing, and understanding financial statements.
-
Data Analysis: Many data analysis tasks involve working with fractions and proportions. Comparing fractions is essential for interpreting and communicating findings.
Frequently Asked Questions (FAQ)
Q1: Is there a shortcut for comparing fractions with different denominators?
A1: While there isn't a universally applicable shortcut, estimating can help. If the denominators are relatively close and the numerators are significantly different, a quick estimation can often suffice. However, using the common denominator or decimal conversion methods is always the most reliable approach for accuracy.
Q2: What if the fractions have very large denominators?
A2: For fractions with very large denominators, the common denominator method might become cumbersome. In such cases, converting to decimals is often a more efficient method. Calculators are also helpful for simplifying calculations with large numbers.
Q3: Can I compare fractions using cross-multiplication?
A3: Yes, cross-multiplication is a useful technique for comparing fractions. To compare a/b and c/d, we cross-multiply: ad and bc. If ad > bc, then a/b > c/d. This method is essentially a shortcut to finding a common denominator and comparing numerators.
Q4: Why is understanding fraction comparison important?
A4: Understanding fraction comparison is a fundamental skill that underpins many advanced mathematical concepts. It is crucial for problem-solving in various fields, from everyday tasks to specialized professions. Proficiency in fraction comparison improves numerical reasoning and analytical skills.
Conclusion: Mastering the Art of Fraction Comparison
This article has explored various methods for comparing fractions, emphasizing the importance of understanding the underlying principles. Whether you use the common denominator method, visual representation, or decimal conversion, the key is to choose the method you find most comfortable and reliable. Remember, mastering fraction comparison is not just about getting the right answer; it's about developing a deeper understanding of numbers and their relationships, a skill that extends far beyond simple fraction comparisons. Practicing these methods with different fractions will solidify your understanding and build your confidence in tackling more complex mathematical problems. With consistent practice, you’ll become proficient in comparing fractions and apply this essential skill to various real-world situations.
Latest Posts
Latest Posts
-
What 25 Percent Of 100
Sep 18, 2025
-
9 7 As A Decimal
Sep 18, 2025
-
8000 Square Feet To Meters
Sep 18, 2025
-
Total Sum Of Squares Calculator
Sep 18, 2025
-
3 4 Divided By 1
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about Whats Bigger 1/8 Or 3/16 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.