Write .03 As A Percent
saludintensiva
Sep 16, 2025 · 5 min read
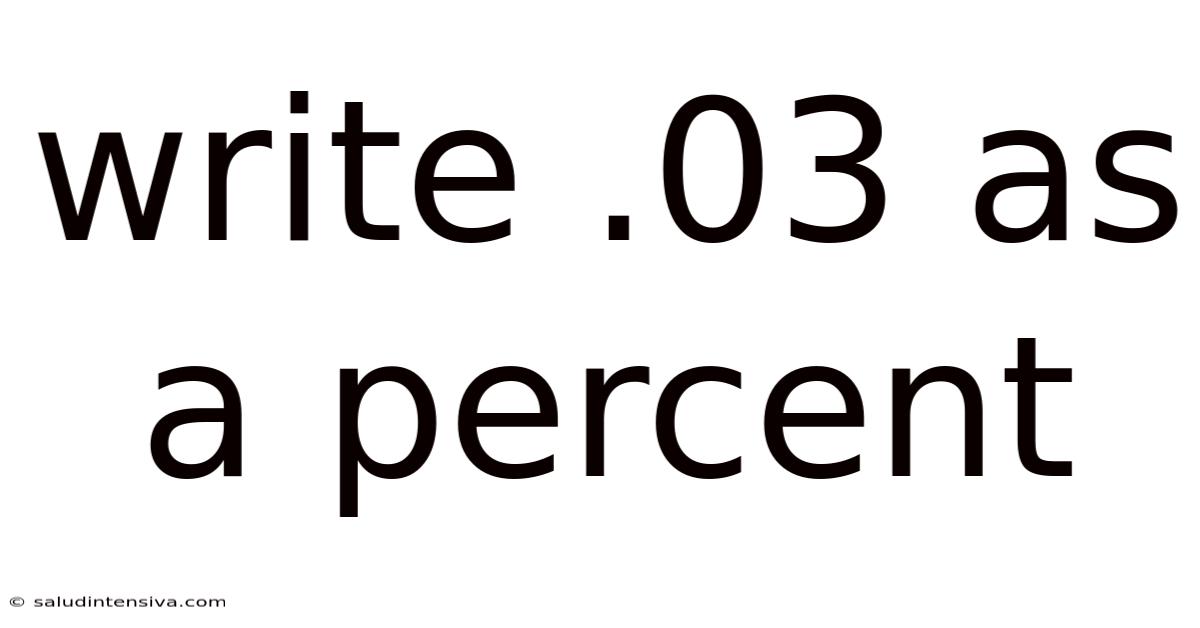
Table of Contents
Writing 0.03 as a Percent: A Comprehensive Guide
Converting decimals to percentages is a fundamental skill in mathematics, frequently used in various fields from finance and statistics to everyday life. This article will comprehensively explore how to write 0.03 as a percent, explaining the underlying concepts and providing practical examples to solidify your understanding. We'll delve into the process, explore related concepts, and address frequently asked questions, ensuring a thorough grasp of decimal-to-percentage conversion.
Understanding Decimals and Percentages
Before diving into the conversion process, let's refresh our understanding of decimals and percentages. A decimal is a number that represents a fraction where the denominator is a power of 10 (e.g., 10, 100, 1000). The decimal point separates the whole number part from the fractional part. For instance, 0.03 signifies three hundredths, or 3/100.
A percentage, denoted by the symbol %, represents a fraction of 100. It indicates "out of 100" or "per hundred." For example, 50% means 50 out of 100, which is equivalent to 50/100 or 1/2.
Converting 0.03 to a Percentage
The conversion from decimal to percentage is straightforward. To express a decimal as a percentage, we simply multiply it by 100 and add the percent symbol (%). This is because percentages are essentially fractions with a denominator of 100.
Therefore, to write 0.03 as a percent:
0.03 * 100% = 3%
Thus, 0.03 is equivalent to 3%.
The Underlying Mathematics: Fractions, Decimals, and Percentages
Let's examine the mathematical relationship between fractions, decimals, and percentages using the example of 0.03.
-
Fraction: 0.03 can be expressed as the fraction 3/100. This is because the decimal point indicates the place value; the '3' is in the hundredths place.
-
Decimal: The decimal representation, 0.03, directly reflects the fraction 3/100.
-
Percentage: To convert the fraction 3/100 to a percentage, we multiply the numerator (3) by 100% and divide by the denominator (100). (3 * 100%) / 100 = 3%. This highlights the inherent relationship: a percentage is simply a fraction expressed as "parts per hundred".
Practical Applications: Real-world Examples
Understanding decimal-to-percentage conversion is crucial in various real-world scenarios. Here are a few examples:
-
Finance: Calculating interest rates, discounts, or tax amounts often involves converting decimals to percentages. A 0.03 interest rate on a loan translates to a 3% annual interest.
-
Statistics: Representing data proportions and probabilities frequently involves percentages. If 0.03 of a population has a particular characteristic, it means 3% of the population possesses that characteristic.
-
Science: Expressing experimental results, measurement errors, or concentration levels often requires converting decimals to percentages. A solution with a 0.03 concentration of solute can be expressed as a 3% solution.
-
Everyday Life: Discount percentages in stores, the success rate of a task, or the portion of a task completed are examples of percentages encountered in daily life.
Working with Larger and Smaller Decimals
The method remains consistent even when dealing with decimals larger or smaller than 0.03:
-
Larger Decimals: For instance, to convert 0.75 to a percentage: 0.75 * 100% = 75%
-
Smaller Decimals: To convert 0.005 to a percentage: 0.005 * 100% = 0.5%
Converting Percentages to Decimals: The Reverse Process
It's equally important to understand the reverse process – converting percentages back to decimals. This involves dividing the percentage by 100.
For example, to convert 3% back to a decimal:
3% / 100 = 0.03
This reciprocal relationship reinforces the understanding of the equivalence between decimals and percentages.
Beyond the Basics: Advanced Applications
The concept of converting decimals to percentages extends to more complex scenarios involving:
-
Compound Interest: Calculating compound interest involves repeatedly applying percentage changes, requiring a strong understanding of decimal-to-percentage conversions.
-
Statistical Analysis: Statistical calculations, such as calculating standard deviations or confidence intervals, often require converting decimals representing probabilities to percentages for easier interpretation.
-
Financial Modeling: Developing financial models for forecasting or risk assessment involves extensive use of decimal-to-percentage conversions.
Frequently Asked Questions (FAQ)
Q: Is it always necessary to multiply by 100% when converting a decimal to a percentage?
A: Yes, multiplying by 100% is essential because a percentage represents parts per hundred. This multiplication essentially scales the decimal to express it as a fraction of 100.
Q: Can I convert a percentage directly to a fraction without going through the decimal form?
A: Yes, you can. To convert a percentage to a fraction, simply write the percentage number as the numerator and 100 as the denominator. For example, 3% becomes 3/100. This can then be simplified if needed.
Q: What if I have a decimal with a whole number part (e.g., 2.03)? How do I convert that to a percentage?
A: The process is the same. Multiply the entire decimal by 100%: 2.03 * 100% = 203%. This indicates 203 parts per hundred, which is greater than 100%.
Q: Why is understanding decimal-to-percentage conversion important?
A: It's crucial for interpreting data, solving problems, and making informed decisions in various fields, as highlighted by the numerous applications discussed previously. It is a fundamental building block in higher-level mathematical concepts and practical applications.
Conclusion
Converting 0.03 to a percentage, yielding 3%, is a seemingly simple task, yet it embodies a fundamental mathematical concept with far-reaching implications. By understanding the underlying relationship between fractions, decimals, and percentages, and by mastering the conversion process, you equip yourself with a valuable tool applicable in numerous academic, professional, and everyday scenarios. The ability to seamlessly move between these different numerical representations is vital for effective communication and problem-solving across various disciplines. Remember the core principle: percentages express parts per hundred, and the conversion process simply adjusts the decimal value to reflect this scale.
Latest Posts
Latest Posts
-
2 Divided By 1 3
Sep 16, 2025
-
Pipe Cross Sectional Area Calculator
Sep 16, 2025
-
17 18 As A Decimal
Sep 16, 2025
-
Random Number Generator 1 14
Sep 16, 2025
-
Calculating Cubic Yards Of Sand
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about Write .03 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.