X 2 6x 12 Factored
saludintensiva
Sep 21, 2025 · 5 min read
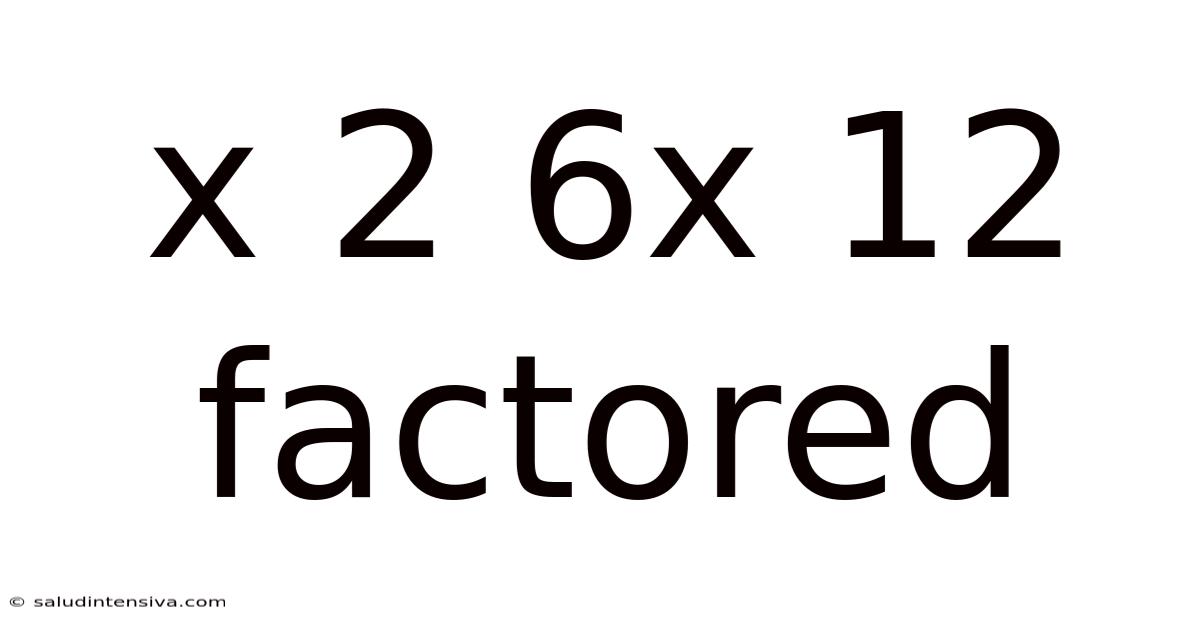
Table of Contents
Factoring Quadratic Expressions: A Deep Dive into x² + 6x + 12
Factoring quadratic expressions is a fundamental skill in algebra. It's the process of rewriting a quadratic expression (a polynomial of degree two) as a product of simpler expressions. This article will provide a comprehensive guide to factoring x² + 6x + 12, exploring various methods and delving into the underlying mathematical principles. We'll also address common misconceptions and answer frequently asked questions to build a strong foundation in this crucial algebraic concept.
Introduction: Understanding Quadratic Expressions
A quadratic expression is typically written in the form ax² + bx + c, where 'a', 'b', and 'c' are constants, and 'x' is the variable. Our specific example, x² + 6x + 12, fits this form with a = 1, b = 6, and c = 12. Factoring this expression involves finding two binomial expressions whose product equals the original quadratic. This process is crucial for solving quadratic equations, simplifying algebraic expressions, and understanding various mathematical concepts.
Attempting to Factor x² + 6x + 12 using Traditional Methods
The most common method for factoring quadratic expressions involves finding two numbers that add up to 'b' (the coefficient of x) and multiply to 'ac' (the product of the coefficients of x² and the constant term). Let's apply this method to x² + 6x + 12:
We need two numbers that add up to 6 and multiply to 12 (since a=1). Let's list the factor pairs of 12:
- 1 and 12
- 2 and 6
- 3 and 4
None of these pairs add up to 6. This indicates that x² + 6x + 12 cannot be factored using integers. This doesn't mean the expression is prime or unfactorable; it simply means it doesn't factor neatly into expressions with integer coefficients.
Exploring the Discriminant: A Deeper Understanding
The discriminant of a quadratic equation (ax² + bx + c = 0) is given by the formula b² - 4ac. The discriminant tells us about the nature of the roots (solutions) of the quadratic equation and indirectly influences the factorability of the expression.
For our expression, x² + 6x + 12:
a = 1, b = 6, c = 12
Discriminant = 6² - 4 * 1 * 12 = 36 - 48 = -12
Since the discriminant is negative, the quadratic equation x² + 6x + 12 = 0 has no real roots. This directly implies that the quadratic expression cannot be factored into real linear factors. Real roots are crucial for obtaining factors using integer or rational coefficients.
Factoring using Complex Numbers
While the expression doesn't factor using real numbers, it can be factored using complex numbers. Complex numbers are numbers of the form a + bi, where 'a' and 'b' are real numbers and 'i' is the imaginary unit (√-1).
To factor using complex numbers, we can use the quadratic formula to find the roots of the equation x² + 6x + 12 = 0:
x = [-b ± √(b² - 4ac)] / 2a
x = [-6 ± √(-12)] / 2
x = [-6 ± 2i√3] / 2
x = -3 ± i√3
Therefore, the roots are x₁ = -3 + i√3 and x₂ = -3 - i√3. These are complex conjugate roots. Using these roots, we can express the factored form as:
(x - (-3 + i√3))(x - (-3 - i√3)) = (x + 3 - i√3)(x + 3 + i√3)
Completing the Square: An Alternative Approach
Completing the square is another method to manipulate quadratic expressions. While it doesn't directly yield a factored form with integer coefficients in this case, it provides valuable insight:
- Group the x terms: (x² + 6x) + 12
- Complete the square: To complete the square for x² + 6x, we take half of the coefficient of x (6/2 = 3), square it (3² = 9), and add and subtract it inside the parentheses: (x² + 6x + 9 - 9) + 12
- Rewrite as a perfect square: (x + 3)² - 9 + 12 = (x + 3)² + 3
This shows that the expression can be rewritten as (x + 3)² + 3, which represents a parabola shifted 3 units to the left and 3 units up. This form highlights the expression's vertex and its parabola shape. While not factored in the traditional sense, it's a useful alternative representation.
Graphical Representation and the Significance of the Discriminant
Graphing the quadratic function y = x² + 6x + 12 visually demonstrates why it cannot be factored with real numbers. The parabola opens upwards (since the coefficient of x² is positive) and its vertex lies above the x-axis. This means the parabola never intersects the x-axis, indicating that there are no real roots, hence no real linear factors. The negative discriminant confirms this graphical observation.
Frequently Asked Questions (FAQ)
-
Q: Is it always possible to factor a quadratic expression?
- A: No. While many quadratic expressions can be factored using integers or rational numbers, some, like x² + 6x + 12, cannot be factored using real numbers. However, they can always be factored using complex numbers.
-
Q: What if I get a different factored form using a different method?
- A: The factored form might appear different due to the order of the factors or the use of equivalent expressions, but they should be algebraically equivalent to the same quadratic expression when multiplied out.
-
Q: Why is factoring important?
- A: Factoring is a cornerstone of algebra. It's essential for solving quadratic equations, simplifying complex algebraic expressions, and understanding various mathematical concepts like conic sections and calculus.
-
Q: Are there other methods to solve quadratic equations besides factoring?
- A: Yes, the quadratic formula and completing the square are alternative methods to find the roots (solutions) of a quadratic equation, even if factoring is not directly applicable.
Conclusion: Embracing the Limitations and Expanding Understanding
While x² + 6x + 12 cannot be factored using real numbers, this shouldn't be viewed as a limitation. Instead, it provides an opportunity to deepen our understanding of quadratic expressions, the discriminant, complex numbers, and alternative algebraic manipulation techniques. By exploring different methods and understanding the underlying principles, we build a robust foundation for tackling more complex algebraic problems. The inability to factor this particular expression using real numbers highlights the richness and nuances of the algebraic world and encourages a more thorough and nuanced approach to problem-solving. Remember, the quest for understanding is a continuous journey; each challenge encountered offers valuable learning opportunities.
Latest Posts
Latest Posts
-
1 13 As A Percent
Sep 21, 2025
-
Convert Gal To Cubic Feet
Sep 21, 2025
-
What 45 Celsius In Fahrenheit
Sep 21, 2025
-
What Is 15 Of 48
Sep 21, 2025
-
12 1000 As A Decimal
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about X 2 6x 12 Factored . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.