X Sqrt 1 X 2
saludintensiva
Sep 20, 2025 · 6 min read
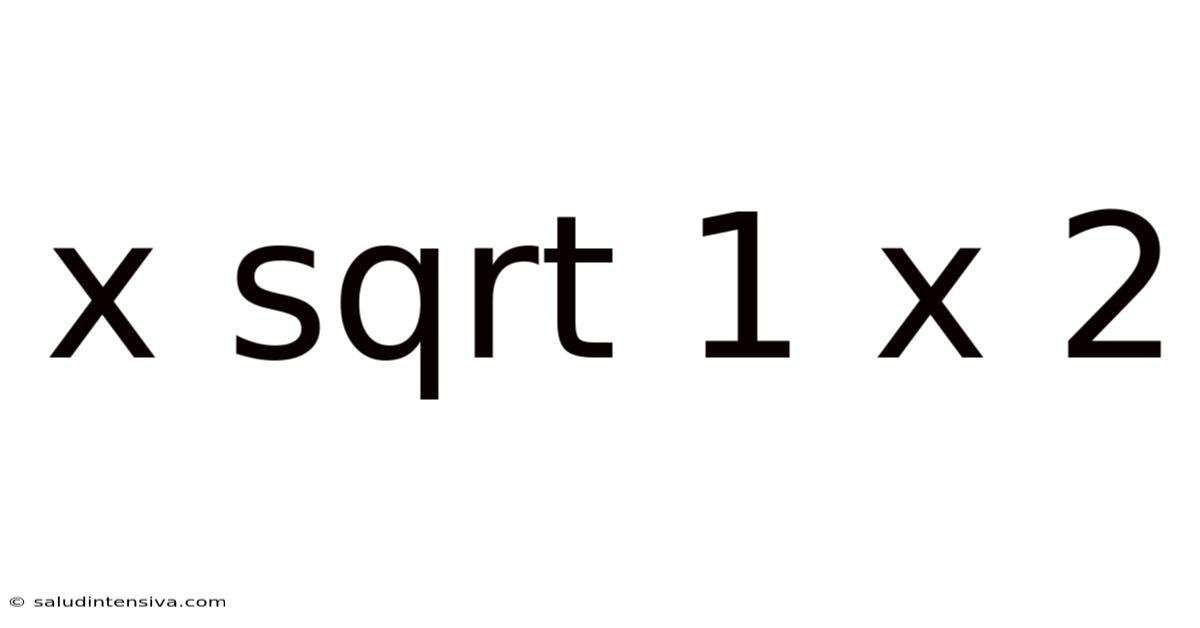
Table of Contents
Decoding the Mystery: x√(1+x²)
This article delves into the intricacies of the mathematical expression x√(1+x²), exploring its properties, applications, and the fascinating connections it holds within various mathematical fields. We will unravel its meaning, explore its behavior under different conditions, and examine its significance in calculus, geometry, and beyond. Understanding this seemingly simple expression opens doors to a deeper appreciation of more complex mathematical concepts.
Introduction: Unveiling the Expression
At first glance, x√(1+x²) might appear straightforward. However, its simplicity belies a rich mathematical tapestry. This expression represents a function of x, where the value of the function depends entirely on the input value of x. The core elements are:
- x: The independent variable, representing any real number.
- √(1+x²): The square root of the sum of 1 and the square of x. This part introduces a non-linear element to the function, impacting its behavior significantly.
- Multiplication: The final step involves multiplying x by the square root term. This interaction creates a function with unique characteristics.
Understanding this expression involves examining how the square root term modifies the behavior of x and vice versa. We'll explore this interaction in detail throughout the article.
Exploring the Behavior of x√(1+x²)
The expression's behavior changes dramatically depending on the value of x. Let's consider several cases:
- x = 0: When x is 0, the expression simplifies to 0√(1+0²) = 0.
- x > 0: As x increases positively, the term √(1+x²) grows, but at a slower rate than x². Consequently, the overall function value increases, but at a non-linear rate. The growth accelerates as x becomes larger.
- x < 0: When x is negative, the square root term remains positive, while x becomes negative. Therefore, the entire expression becomes negative. The magnitude of the expression follows the same pattern as the positive x values, increasing in absolute value as |x| grows larger.
- Large Values of x: For extremely large (positive or negative) values of x, the '1' within the square root becomes insignificant compared to x². The expression approximates x√(x²) which simplifies to x|x|. This demonstrates that the function's growth resembles a cubic function for large values of x.
This analysis reveals that the function isn't simply a linear relationship; it's far more complex, involving both linear and non-linear components intertwined.
Graphical Representation and Analysis
Visualizing the function is crucial to understanding its behavior. Plotting the function on a graph reveals a curve that passes through the origin (0,0). The curve is symmetric with respect to the origin because f(-x) = -f(x), indicating an odd function. This symmetry highlights the behavior described earlier: negative values of x produce negative function values with the same magnitude as their positive counterparts.
The curve's steepness increases as |x| increases, indicating the accelerating growth for larger absolute values of x. Analyzing the slope of the curve at different points can reveal valuable information about the function's rate of change.
Calculus: Derivatives and Applications
Applying calculus provides further insight into the function's properties. The derivative of x√(1+x²) provides information about the slope (instantaneous rate of change) of the function at any given point:
To find the derivative, we can use the product rule and the chain rule of differentiation:
Let f(x) = x√(1+x²) = x(1+x²)^(1/2)
Then f'(x) = (1)(1+x²)^(1/2) + x * (1/2)(1+x²)^(-1/2) * 2x
Simplifying, we get:
f'(x) = √(1+x²) + x²(1+x²)^(-1/2) = √(1+x²) + x² / √(1+x²) = (1+2x²) / √(1+x²)
The derivative shows that the slope is always positive for all real x, indicating that the function is monotonically increasing. The second derivative will reveal information about the concavity of the curve.
The derivative has various applications: finding tangent lines, optimization problems (finding maximum or minimum values), and analyzing the function's rate of change.
Geometric Interpretations and Applications
The expression x√(1+x²) appears in several geometric contexts. Consider a right-angled triangle with legs of length x and 1. The hypotenuse, according to the Pythagorean theorem, has length √(1+x²). Then, the expression x√(1+x²) can be interpreted as the product of one leg and the hypotenuse of this right-angled triangle. This connection provides a geometric visualization of the expression's magnitude.
This geometric interpretation can be applied to various problems in geometry, such as calculating areas, volumes, and distances within three-dimensional space. For example, it can be used to derive formulas relating the radius of a circle to the length of a chord or to calculate the length of a diagonal of a rectangle in a specific context.
Advanced Applications in Physics and Engineering
The expression x√(1+x²) appears in various physics and engineering applications, often in contexts involving:
- Relativistic Physics: In special relativity, the expression can emerge when dealing with calculations involving velocity and momentum.
- Mechanics: It could appear in problems related to forces, work, and energy in systems involving non-linear relationships.
- Electromagnetism: Certain electromagnetic calculations may involve this expression when considering the field strength or potential due to complex configurations of charges or currents.
These are just a few examples; its presence in these fields stems from its ability to represent non-linear relationships between variables.
Frequently Asked Questions (FAQ)
Q1: Is x√(1+x²) always positive?
A1: No. While √(1+x²) is always positive for real x, the overall expression becomes negative when x is negative.
Q2: Does this expression have any limits as x approaches infinity?
A2: As x approaches positive or negative infinity, the expression behaves approximately like x|x|, which is unbounded.
Q3: How can I simplify x√(1+x²)?
A3: Simplification depends on the context. For large x, it approximates to x|x|. However, there is no simple algebraic simplification for all values of x.
Q4: What is the integral of x√(1+x²)?
A4: This requires a substitution. Let u = 1 + x², then du = 2x dx. The integral then becomes (1/2)∫u^(1/2) du = (1/3)u^(3/2) + C = (1/3)(1+x²)^(3/2) + C, where C is the constant of integration.
Conclusion: A Deeper Understanding
The seemingly simple mathematical expression x√(1+x²) reveals a wealth of mathematical richness. Through careful analysis, we have uncovered its behavior across different values of x, explored its graphical representation, applied calculus to understand its rate of change and its geometric interpretations and touched upon its applications within various fields of science and engineering. By unraveling this expression, we have broadened our understanding of mathematical concepts, showcasing the elegance and complexity inherent even in apparently straightforward mathematical functions. This deeper understanding underscores the importance of exploring seemingly simple expressions to reveal hidden complexities and unexpected connections within the world of mathematics. It encourages further exploration into the world of non-linear functions and their significant roles in various scientific and engineering disciplines.
Latest Posts
Latest Posts
-
A Cubed B Cubed
Sep 20, 2025
-
270 Degrees Celsius In Fahrenheit
Sep 20, 2025
-
21 Cm How Many Inches
Sep 20, 2025
-
9600 Sq Ft To Acres
Sep 20, 2025
-
Is Ten A Perfect Square
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about X Sqrt 1 X 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.