X Squared Multiplied By X
saludintensiva
Sep 22, 2025 · 5 min read
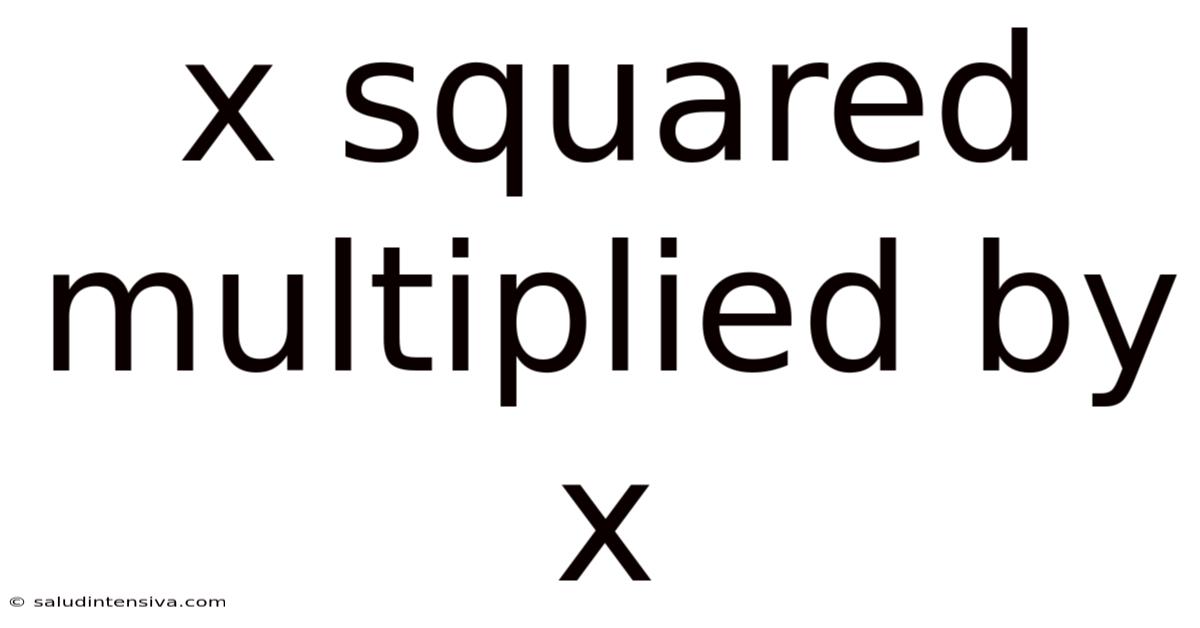
Table of Contents
Understanding x² Multiplied by x: A Deep Dive into Algebraic Multiplication
This article explores the fundamental algebraic operation of multiplying x squared (x²) by x. We'll break down the process step-by-step, explain the underlying mathematical principles, and address common questions and misconceptions. Whether you're a beginner struggling with algebraic concepts or seeking a refresher on fundamental rules, this guide will provide a comprehensive understanding of this seemingly simple yet crucial operation. We will cover the rules of exponents, practical examples, and applications in more complex algebraic equations.
Introduction to Exponents and Variables
Before diving into the multiplication of x² by x, let's refresh our understanding of exponents and variables. In algebra, a variable is a symbol, usually a letter like x, y, or z, that represents an unknown or unspecified number. An exponent indicates how many times a base number is multiplied by itself. For example:
- x² (x squared) means x * x
- x³ (x cubed) means x * x * x
- x⁴ (x to the power of four) means x * x * x * x
The number being multiplied is called the base, and the small number written above and to the right is the exponent or power.
Multiplying x² by x: The Rule of Exponents
The core principle governing the multiplication of x² by x lies in the rules of exponents. Specifically, when multiplying terms with the same base, we add their exponents. Let's apply this to our problem:
x² * x = x²⁺¹ = x³
This is because x² represents x * x, and multiplying this by another x gives us x * x * x, which is x³. Therefore, x squared multiplied by x equals x cubed.
Step-by-Step Explanation
Let's break down the process into clear, concise steps:
-
Identify the base and exponents: In the expression x² * x, the base is 'x'. The exponents are 2 and 1 (remember that x is the same as x¹).
-
Apply the rule of exponents for multiplication: When multiplying terms with the same base, add the exponents. In this case, 2 + 1 = 3.
-
Write the final answer: The result of x² * x is x³.
Visual Representation
Understanding the concept visually can be helpful. Imagine x² as a square with sides of length x. Its area would be x * x = x². Now, imagine multiplying this square by x. This can be interpreted as extending the square into a cube with sides of length x. The volume of this cube is x * x * x = x³, demonstrating the result of the multiplication.
Practical Examples
Let's explore a few practical examples to solidify our understanding:
-
Example 1: 2x² * x = 2x³ (The coefficient 2 remains unchanged; we only add the exponents of the x terms)
-
Example 2: (3x²) * (4x) = 12x³ (Multiply the coefficients 3 and 4, and then add the exponents of x)
-
Example 3: x²y * x = x³y (The exponent of 'y' remains 1 because it's not involved in the multiplication with x)
-
Example 4: (5x²)(2xy²) = 10x³y² (Multiply the coefficients and add the exponents of corresponding variables)
These examples illustrate how the rule of exponents applies in different scenarios, incorporating coefficients and multiple variables.
Extending the Concept: More Complex Expressions
The principle extends to more complex expressions involving multiple variables and higher exponents. For instance:
- x³ * x⁴ = x⁷ (3 + 4 = 7)
- x⁵ * x⁻² = x³ (5 + (-2) = 3; remember rules for negative exponents)
- (2x³y²)(3x²y⁴) = 6x⁵y⁶ (multiply coefficients, add exponents of like variables)
The Significance of Understanding x² * x
Mastering the concept of multiplying x² by x is crucial for progressing in algebra and other branches of mathematics. It forms the foundation for:
-
Polynomial manipulation: Polynomials are expressions involving variables and their powers. Understanding this basic multiplication is key to simplifying, expanding, and factoring polynomials.
-
Calculus: Calculus heavily relies on algebraic manipulation, and this fundamental operation appears repeatedly in differentiation and integration.
-
Solving Equations: Solving equations often involves manipulating algebraic expressions, and knowing how to multiply terms with the same base is essential.
-
Problem Solving in various fields: Algebra and its principles are applied in various fields such as physics, engineering, economics, and computer science, making this fundamental understanding critical.
Frequently Asked Questions (FAQ)
Q1: What happens if I multiply x² by x²?
A1: Following the rule of exponents, x² * x² = x⁴ (2 + 2 = 4).
Q2: Can I multiply x² by a number like 5?
A2: Yes. The multiplication becomes 5x². The coefficient is multiplied by the number, but the exponent of x remains unchanged.
Q3: What if one of the terms is negative?
A3: The rule of exponents still applies. For instance, -x² * x = -x³. Remember to consider the sign of the coefficient when performing the multiplication.
Q4: What about multiplying x² by something other than x, like y?
A4: You simply get x²y. The variables are multiplied, but their exponents are not added because they are not the same base.
Q5: How does this relate to area and volume?
A5: As mentioned earlier, visualizing x² as the area of a square and x³ as the volume of a cube provides a geometric interpretation of the multiplication. It helps solidify the understanding of the increase in dimensionality when you multiply by x.
Conclusion: A Foundation for Further Learning
Understanding the multiplication of x² by x, based on the fundamental rules of exponents, is a crucial stepping stone in mastering algebraic concepts. This seemingly simple operation underpins more complex algebraic manipulations and is foundational to numerous applications in various fields of study. Through step-by-step explanations, visual representations, and practical examples, we've built a comprehensive understanding of this core principle. By mastering this foundational concept, you're well-equipped to tackle more challenging algebraic problems and advance your mathematical skills. Remember to practice regularly and seek help when needed – your mathematical journey is a process of continuous learning and growth. The more you practice, the more intuitive these concepts will become, ultimately leading to a deeper understanding of algebra and its applications.
Latest Posts
Latest Posts
-
Convert 110 Pounds To Kilos
Sep 22, 2025
-
3x 1 10x X 4
Sep 22, 2025
-
Is 3 A Whole Number
Sep 22, 2025
-
1 3 Of A Foot
Sep 22, 2025
-
What Is A Rate Ratio
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about X Squared Multiplied By X . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.