1 1 2 X 5
saludintensiva
Sep 20, 2025 · 6 min read
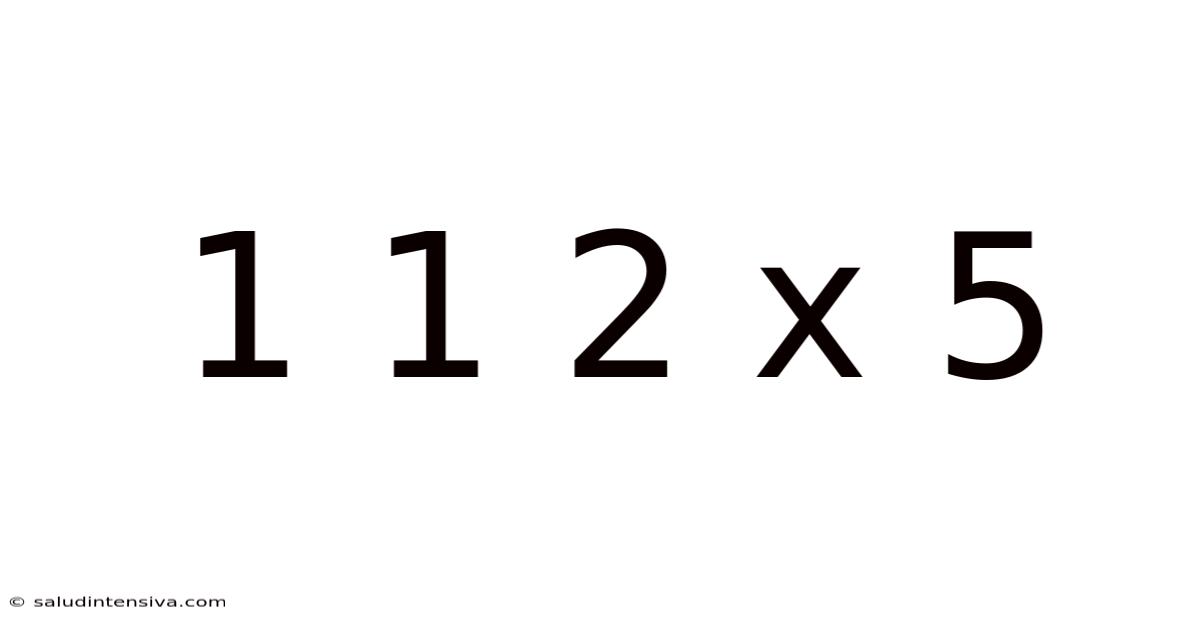
Table of Contents
Decoding 1 1 2 x 5: Exploring the Multifaceted Aspects of a Simple Equation
This article delves into the seemingly simple equation "1 1 2 x 5," exploring its various interpretations, applications, and underlying mathematical principles. While the equation itself might appear elementary at first glance, its ambiguity allows us to explore fundamental concepts in arithmetic, algebra, order of operations, and even the importance of clear communication in mathematics. We'll unpack the different possible meanings, discuss the implications of each interpretation, and ultimately demonstrate the significance of precise notation in problem-solving.
Understanding the Ambiguity: Why This Equation Matters
The equation "1 1 2 x 5" is deliberately ambiguous. The lack of clear operational symbols (+, -, ×, ÷) between the numbers creates multiple valid interpretations, depending on how we choose to group the numbers and apply the order of operations. This ambiguity highlights a crucial aspect of mathematics: the importance of precise notation. A seemingly simple equation can lead to drastically different results if the intended operations are not clearly specified. This is particularly relevant in programming, engineering, and any field requiring precise calculations where misinterpretations can have significant consequences.
Possible Interpretations and Their Solutions
Let's explore the most plausible interpretations of "1 1 2 x 5," and solve each one to illustrate the impact of different operational orderings:
Interpretation 1: Sequential Addition and Multiplication
This interpretation assumes a sequence of operations: addition first, followed by multiplication. We can rewrite the equation as:
(1 + 1 + 2) x 5 = 4 x 5 = 20
Here, we add 1, 1, and 2 together before multiplying the result by 5. This is a straightforward interpretation, easy to understand and solve.
Interpretation 2: Implicit Multiplication and Addition
This interpretation treats the adjacent numbers as implicitly multiplied. We can rewrite this as:
(1 * 1) + (2 * 5) = 1 + 10 = 11
Here, the equation is solved by performing multiplications first (1 x 1 and 2 x 5) before adding the resulting values. This showcases the significant impact of order of operations.
Interpretation 3: Concatenation and Multiplication
While less common mathematically, one could interpret the numbers as concatenation (stringing numbers together) followed by multiplication:
(112) x 5 = 560
This is a less conventional interpretation, but highlights the need to clearly define the context in which an equation is presented. In programming languages, for instance, this sort of string manipulation is fairly common.
Interpretation 4: Other Possible Combinations
Given the ambiguity, we could even conceive of more complex interpretations involving other mathematical operations or groupings. For example, we could potentially consider:
- 1 + (1 + 2) x 5 = 1 + 15 = 16
- 1 + 1 + (2 x 5) = 1 + 1 + 10 = 12
- (1 + 1) x (2 x 5) = 2 x 10 = 20
The variety of possible results underscore the crucial role of clear notation and the application of established order of operations.
The Order of Operations (PEMDAS/BODMAS): A Cornerstone of Arithmetic
To avoid the ambiguity inherent in "1 1 2 x 5," we rely on the order of operations, often remembered by acronyms like PEMDAS (Parentheses, Exponents, Multiplication and Division, Addition and Subtraction) or BODMAS (Brackets, Orders, Division and Multiplication, Addition and Subtraction). These mnemonics help us determine the sequence in which operations should be performed.
Without parentheses or other grouping symbols to explicitly define the order, we typically follow PEMDAS/BODMAS. In the absence of parentheses, multiplication generally precedes addition. However, the ambiguity in "1 1 2 x 5" arises precisely because the operations aren’t clearly delineated.
The Importance of Clear Notation in Mathematics and Beyond
The ambiguity of "1 1 2 x 5" serves as a valuable lesson in the importance of clear mathematical notation. Ambiguous notation can lead to errors, misunderstandings, and even costly mistakes in real-world applications. Precision in mathematical communication is paramount, especially in fields like:
- Engineering: Incorrect calculations due to ambiguous notation can have severe consequences, potentially leading to structural failures or malfunctions.
- Computer Programming: Programming languages rely on strict syntax and operational precedence. Ambiguous code can result in program crashes or unexpected outputs.
- Finance: Errors in financial calculations can have significant financial repercussions.
- Science: Precise notation ensures accurate data representation and analysis in scientific research.
Extending the Concept: Algebraic Representation and Generalization
We can also extend our analysis to explore how this equation could be generalized algebraically. Let's represent the numbers as variables:
a b c x d
Now, we can explore different interpretations and their algebraic expressions. For instance:
- (a + b + c) x d
- (a x b) + (c x d)
- (abc) x d
This algebraic approach allows us to explore a wider range of possibilities and provides a more formal framework for analyzing the different interpretations.
Applications in Education and Problem-Solving
The seemingly simple equation "1 1 2 x 5" offers a valuable teaching tool in mathematics education. It can be used to:
- Reinforce the order of operations: Students can practice applying PEMDAS/BODMAS to different interpretations of the equation.
- Highlight the importance of clear notation: The ambiguity of the equation underscores the need for precision in mathematical writing.
- Encourage critical thinking and problem-solving: Students can explore different interpretations and justify their reasoning.
- Develop algebraic thinking: By representing the numbers as variables, students can start to develop algebraic thinking and generalization skills.
Frequently Asked Questions (FAQ)
Q: What is the "correct" answer to 1 1 2 x 5?
A: There is no single "correct" answer without clarifying the intended operations. The equation is deliberately ambiguous, and the solution depends on the interpretation of the operations.
Q: Why is this equation considered ambiguous?
A: The equation is ambiguous because it lacks explicit operational symbols between the numbers. This lack of clarity leads to multiple valid interpretations based on different applications of order of operations.
Q: How can I avoid ambiguity in my mathematical expressions?
A: Use parentheses or other grouping symbols to explicitly define the order of operations. Be clear and consistent with your notation, and leave no room for interpretation.
Q: What is the significance of this equation in mathematics?
A: This equation serves as a practical example of the importance of clear notation and the consistent application of order of operations. It highlights how ambiguous notation can lead to multiple interpretations and incorrect results.
Conclusion: The Power of Precision
The seemingly simple equation "1 1 2 x 5" reveals a deeper truth about the nature of mathematics: the critical importance of clear and precise notation. While the equation itself is straightforward, its ambiguity presents a valuable opportunity to explore fundamental mathematical concepts, highlight the significance of the order of operations, and underscore the need for clear communication in all fields of quantitative analysis. By understanding the potential interpretations and their solutions, we gain a deeper appreciation for the power of precision in mathematical expression. The lesson learned from this seemingly simple equation transcends its elementary appearance, demonstrating the crucial role precision plays in preventing errors and ensuring accurate results in any field involving numerical calculations.
Latest Posts
Latest Posts
-
Lcm Of 16 And 22
Sep 20, 2025
-
90 Days From 6 6
Sep 20, 2025
-
X 3 X 5 2
Sep 20, 2025
-
Lbf Ft To Kg M
Sep 20, 2025
-
7 16ths Of An Inch
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about 1 1 2 X 5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.